Метод интервалов, решение неравенств
Решение неравенств
Метод интервалов
Перенос знаков
Выбор точек
Система и совокупность
Точка знакопостоянства
Что нельзя делать в неравенстве, даже под пытками:
1) Домножать на знаменатель.
2) Умножать/делить на отрицательное число, не меняя знак.
3) Убирать бездумно логарифм или основание.
Начнем с простого:
Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:
А само значение −4 нам подходит?
Нет, поэтому ставим круглые скобочки ()
Ответ: x ∈ ( −4; +oo).
Разберемся со скобками:
Когда мы включаем точку (корень числителя), или стоят знаки нестрогие (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>, <), скобки круглые «( )».
Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:
Ответ: x ∈ ( 0; +oo).
Следующий пример уже с дробью:
Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:
к.ч. (корни числителя)
к.з. (корни знаменателя)
Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:
Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:
Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>, <), скобки круглые «( )».
Ответ: x ∈ (2; 7].
Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:
Отметим на прямой решение каждого неравенства.
Решением системы «{» является тот участок, который подходит обоим неравенствам.
Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.
Мой любимый пример:
Покажу мастер-класс, как делать не надо. Дома не повторять!
А теперь через метод интервалов разберемся, как сделать правильно:
Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:
В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».
Ответ: x ∈ (−3; 3).
Перейдем к квадратному уравнению:
Разложим на множители и подставим x = 10, чтобы определить знак:
Нам требуются положительные значения:
Второй способ разложить на множители:
Ответ: x ∈ (−oo; −1) ∪ (5; +oo).
А теперь простой, но крайне показательный пример:
Убирать квадрат ни в коем случае нельзя. Простенький контрпример:
Надеюсь, убедил.
Вместо знака больше поставим знак равно и попробуем решить методом интервалов:
Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).
Проверим это:
В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».
Только точка «0» не подходит, 0 > 0 — неверно!
Ответ: x ∈ R \ {0} или x ∈ (−oo; 0) ∪ (0; +oo).
Переходим на новый уровень:
Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)
По методу координат найдем корни числителя и знаменателя:
Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).
Требуется найти промежутки, где выражение больше или равно нулю.
Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.
Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.
Ответ: (−oo; − 6) ∪ {0} ∪ [ 3; +oo).
Дальше интереснее:
По той же схеме корни числителя и знаменателя:
Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:
Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.
Ответ: {−3} ∪ (−2; +oo).
Закрепляем последовательность:
Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?
Подставим x = 10 и расставим знаки:
Ответ: [ −oo; −5) ∪ [ 3; 5).
Все скользкие моменты разобрали, стало понятнее?
Резюме:
- Если знак строгий (>, <), все точки выколотые (в круглые скобки).
- Если знак нестрогий (≥, ≤), корни числителя закрашенные, точки знаменателя выколотые [в квадратные скобки].
- Если корень является решением уравнения четное кол-во раз (2, 4, 6, 8), то в этой точке знак меняться не будет.
- Отдельная точка записывается {в фигурных скобках}.
Нашел ошибку/опечатку — напиши.
Группа с полезной информацией и легким математическим юмором.
Метод интервалов — материалы для подготовки к ЕГЭ по Математике
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
1. Рассмотрим неравенство:
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения.
В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .
, где и — корни квадратного уравнения .
Получим:
Рисуем ось X и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
Нули знаменателя и — выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя).
Напомним, что мы изображаем точку на числовой прямой выколотой (пустой), если соответствующее значение переменной никак не может быть решением неравенства.
В нашем примере точки и выколотые, потому что в них знаменатель обращается в ноль.
Нули числителя и — закрашены, так как неравенство нестрогое. При и наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось X на 5 промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например, и проверим знак выражения в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак .
Следующий промежуток: . Проверим знак при . Получаем, что левая часть поменяла знак на .
. Возьмем . При выражение положительно — следовательно, оно положительно на всем промежутке от до .
При левая часть неравенства отрицательна.
И, наконец, . Подставим и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак .
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: .
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
, или , или , или
(в левой части — дробно-рациональная функция, в правой — нуль).
Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
2. Рассмотрим еще одно неравенство:
Решение:
Снова расставляем точки на оси X. Точки и — выколотые, поскольку это нули знаменателя. Точка — тоже выколота, поскольку неравенство строгое, и значение переменной не может быть решением неравенства.
При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, . Левая часть имеет знак :
При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен.
Левая часть имеет знак :
При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :
Наконец, при все множители положительны, и левая часть имеет знак :
Ответ: .
Почему нарушилось чередование знаков? Потому что при переходе через точку 2 «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку знак выражения в левой части не меняется
. В случае нечётной степени знак, разумеется, меняется.3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Решение:
Левая часть та же, что и в предыдущем примере. Та же будет и картина знаков:
Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
Ответ: .
В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
Решение:
Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения при всех одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех .
Придём к равносильному неравенству:
Решим неравенство методом интервалов. Действуем по алгоритму: числитель левой части равен нулю при а знаменатель обращается в ноль при . Отметим эти точки на координатной прямой. Точки выколоты, потому что неравенство строгое. Эти точки разбивают числовую ось на три интервала.
Найдем знаки на каждом из интервалов. На крайнем правом знак положителен, а дальше знаки чередуются.
Нам нужен «интервал со знаком минус», то есть такой, где Выпишем ответ.
Ответ:
Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Решение:
Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
Мы поступим по-другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
Применим метод интервалов.
Действуем по алгоритму. Отметим на координатной прямой точки и .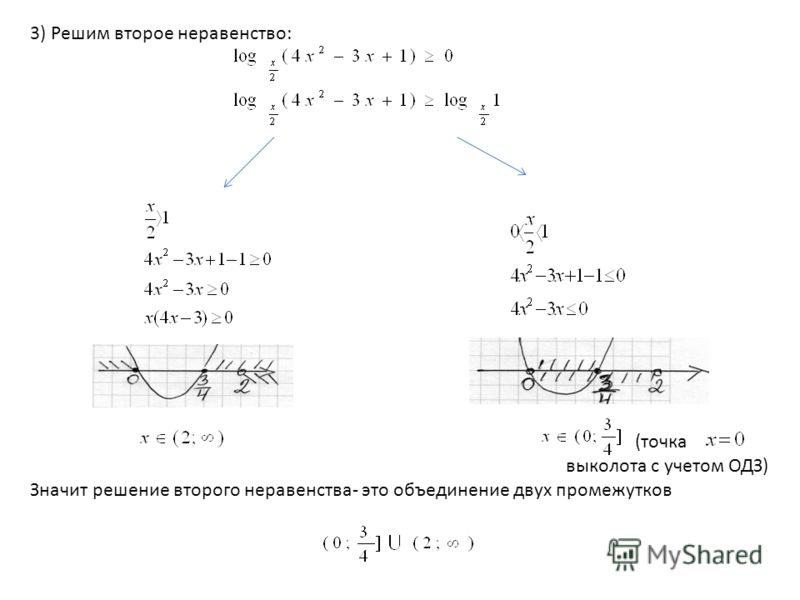
Они выколотые, потому что неравенство строгое. Эти точки разбивают ось Х на три интервала. Расставим знаки на каждом из них.
Ответ:
6.
Решение:
Приведем левую часть неравенства к общему знаменателю и преобразуем числитель:
Применим метод интервалов:
Числитель равен нулю при Знаменатель обращается в ноль при или . Неравенство строгое, поэтому все эти точки на числовой оси отмечаем как пустые.
Если , то . Далее знаки чередуются.
Нам нужны «интервалы со знаком минус». Выпишем их и получим ответ.
Ответ:
7. Решите неравенство
Решение:
Приведем неравенство к виду:
Для этого все перенесем в левую часть, приведем к общему знаменателю и разложим числитель и знаменатель на множители. Применяем формулу разности квадратов и формулу разложения квадратного трехчлена на множители
Получим:
Найдем нули числителя и знаменателя и отметим их на числовой оси:
Выпишем интервалы, где неравенство выполняется, и получим ответ.
Ответ:
8. Решите неравенство:
Решение:
Разложим левую часть неравенства на множители.
Для этого вынесем общий множитель за скобки, а затем воспользуемся формулой:
Получим:
Применим метод интервалов.
Левая часть неравенства обращается в ноль, если , или . Нанесем эти точки на координатную прямую. Все точки закрашенные, так как неравенство нестрогое, в нем присутствует знак «меньше или равно».
Ответ:
9. Решите неравенство:
Решение:
Разложим числитель на множители с помощью группировки:
Знаменатель тоже разложим на множители:
Неравенство примет вид:
Мы видим, что числитель равен нулю при
Знаменатель равен нулю при . Множитель стоит в числителе и в знаменателе, и он не может равняться нулю.
Отметим полученные точки на координатной прямой. Две из них закрашены (это 3 и 1), а две нет (это -1 и -2). Найдем знаки на каждом промежутке.
При переходе через точку знак не меняется, так как множитель присутствует и в числителе, и в знаменателе.
Выпишем ответ.
Ответ:
10. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Напомним, что выражение мы разложили на множители, решив квадратное уравнение:
Неравенство примет вид:
Воспользуемся методом интервалов.
Числитель дроби в левой части неравенства равен нулю, если Знаменатель обращается в ноль, если или . Отметим эти точки на координатной прямой и определим знаки на интервалах.
Ответ:
11. Решите неравенство:
Решение:
Можно сразу применить метод интервалов.
Но лучше, чтобы не запутаться со знаками, умножить обе части неравенства на (-1) и не забыть поменять знак неравенства на противоположный.
Теперь применим метод интервалов.
Отметим на координатной прямой нули числителя и знаменателя и определим знаки на интервалах.
Обратите внимание, что знак не меняется при переходе через точку , так как множитель входит в выражение в левой части неравенства в четной степени.
Ответ:
12. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Сократим на множитель при условии, что .
Здесь мы действуем чуть иначе, чем в задаче 9.
Неравенство равносильно системе:
Решаем второе неравенство системы методом интервалов:
Второму неравенству удовлетворяют точки .
Точка в этот промежуток не входит.
Ответ:
13. Решите неравенство:
Решение:
Разложив числитель на множители, получим:
Применим метод интервалов.
Отметим на числовой оси точки, в которых числитель и знаменатель обращаются в ноль. Обратите внимание, что точки -1 и 5 закрашены, а точки 2 и 4 пустые.
Определим знаки на интервалах.
Знак не меняется при переходе через точку , так как множитель входит в выражение в левой части неравенства в четной степени.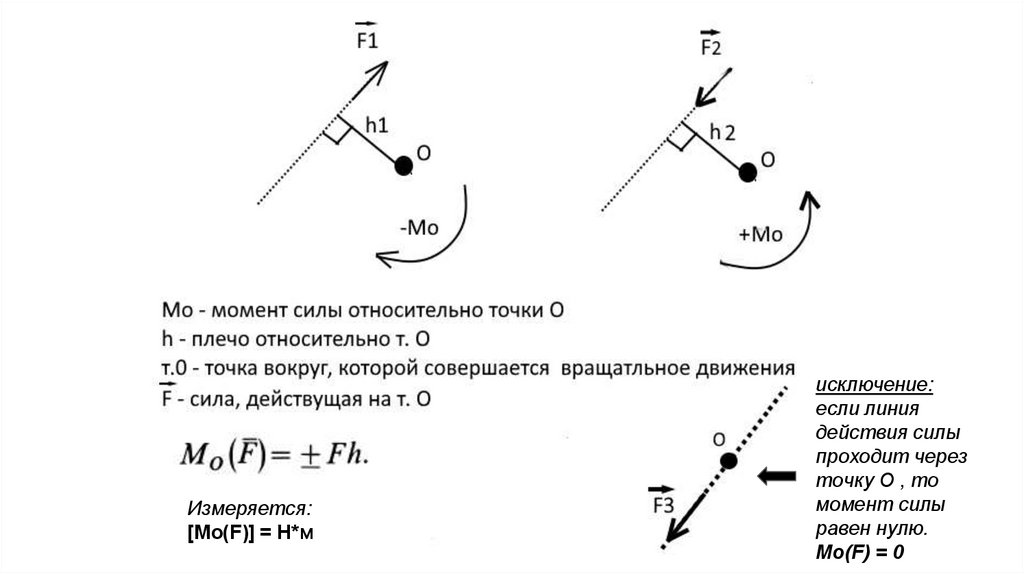
При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.
В ответе запишем интервалы, на которых неравенство выполняется.
Ответ:
14. Решите неравенство:
Разложим числитель и знаменатель на множители, используя формулы сокращенного умножения: суммы и разности кубов, разности квадратов.
Кажется, что неравенство сложное. Попробуем разложить на множители выражения и
Оказывается, что дискриминанты соответствующих квадратных уравнений отрицательны, поэтому и при всех х.
Разделим обе части неравенства на эти положительные выражения.
Получим:
Неравенство равносильно системе:
Решим первое неравенство системы методом интервалов:
Его решением является промежуток [1;4], причем точка в этот промежуток не входит.
Ответ:
Мы показали на различных примерах, как применяется метод интервалов.
Сделаем вывод:
Метод интервалов помогает решать дробно-рациональные неравенства по алгоритму.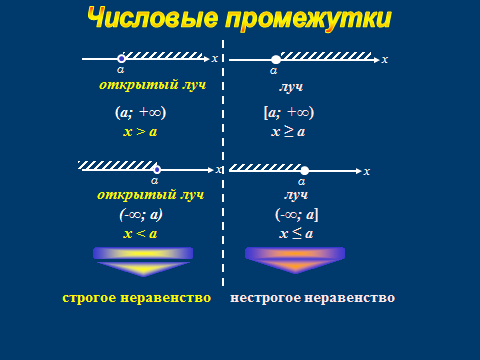
Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.
Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Метод интервалов» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из #cat_parent.
Публикация обновлена:
25.
12.2022
Фотографии, Размещение, Процедура, Уход, Риски, Еще
Какой это тип пирсинга?
Кожный пирсинг также известен как одноточечный пирсинг. Это связано с тем, что у дермалов нет отдельной точки входа и выхода для украшений, в отличие от традиционного пирсинга.
Вместо этого ваш пирсинг сделает одно маленькое отверстие, чтобы «якорь» можно было вставить в средний слой (дерму) вашей кожи. Длина основания анкера обычно составляет 6 или 7 миллиметров, чего достаточно, чтобы закрепить столб.
Настоящее украшение привинчено к верхней части столба. Он сидит на поверхностном слое, придавая вид бусинок на вашей коже.
Хотя кожные украшения располагаются на верхнем слое кожи, кожные украшения не являются поверхностным пирсингом.
Поверхностные отверстия имеют отдельный вход и выход. Они закреплены с помощью штанг в форме открытых скоб. Эта штанга вставляется под кожу. Декоративные накладки ложатся на поверхность кожи.
Кожный пирсинг можно делать в любом месте тела, если участок кожи плоский.
Популярные зоны:
- скулы
- задняя часть шеи
- грудь
- нижняя часть спины
- живот
- бедра
-не обязательно имеет достаточно толстую кожу, чтобы быть закрытой областью удерживайте кожный якорь на месте.
Кожный пирсинг можно сделать с помощью иглы или кожного (кожного) перфоратора. Тип используемых украшений зависит от того, как сделан пирсинг.
Возможные варианты:
- Анкер. Традиционный кожный пирсинг начинается с якоря, который вставляется под кожу. Ваш якорь может иметь закругленное основание или плоские «ножки» с каждой стороны стойки.
- Верх. Как только якорь будет на месте, ваш пирсер завершит якорь выбранным вами типом украшений. Примеры включают металлические шпильки или магнитные драгоценные камни.
- Водолаз. Дайверы имеют заостренные основания с предустановленными украшениями наверху. Ваш мастер по пирсингу будет использовать перфоратор для кожи, чтобы вставить этот тип украшений. В отличие от типичного стиля якоря и топпера, дайверы не взаимозаменяемы.
В отличие от типичного стиля якоря и топпера, дайверы не взаимозаменяемы.Поговорите со своим мастером по пирсингу о следующих вариантах:
- Хирургический титан. Если у вас чувствительная кожа, титан с наименьшей вероятностью вызовет раздражение.
- Хирургическая нержавеющая сталь. Это самый популярный материал, отмечает ТатРинг. Хотя он считается гипоаллергенным, раздражение все же возможно.
- Ниобий. Это еще один гипоаллергенный материал, который вряд ли будет подвергаться коррозии.
- Золото. Для золота важно качество. Придерживайтесь 14-каратного желтого или белого золота во время процесса заживления. Золото выше 18 карат не такое прочное. Позолоченные украшения могут привести к инфекциям и аллергическим реакциям.
Кожный пирсинг обычно стоит от 70 до 100 долларов, по оценкам Cost Helper. Некоторые магазины взимают отдельную плату за украшения.
Это может добавить еще 10-20 долларов к общей стоимости.
Вам также нужно будет учесть чаевые для мастера по пирсингу. По крайней мере 20 процентов является стандартным.
Также узнайте у мастера по пирсингу первоначальные расходы, связанные с последующим уходом, например, солевым раствором.
Кожный пирсинг делается с помощью игл или проколов кожи. Каждый подход включает размещение якоря под кожей.
Для пирсинга кожи иглами:
- Мастер очистит вашу кожу, убедившись, что она полностью стерильна.
- После того, как область высохнет, они пометят вашу кожу ручкой или маркером, чтобы убедиться, что пирсинг сделан в нужном месте.
- Они проткнут кожу иглой и вытащат ее обратно. Это создаст «карман» для фиксации анкера.
- Ваш специалист по пирсингу, скорее всего, будет использовать щипцы, чтобы вставить основание анкера в отверстие. Они будут вдавливать украшение до тех пор, пока оно полностью не окажется под поверхностью вашей кожи.
- После того, как анкер установлен, мастер по пирсингу завинчивает верхнюю часть украшения.
Для пирсинга кожи с помощью дырокола ваш пирсер будет выполнять те же действия, что и выше, за исключением того, что отверстие делается с помощью дырокола вместо иглы. Кожный перфоратор удаляет небольшой кусочек ткани, чтобы создать карман, в котором будет располагаться якорь.
Незначительная боль возможна при любом проколе. Кожные покровы не являются исключением.
То, как вы себя чувствуете во время прокола, зависит от нескольких факторов, таких как:
- место размещения (чем более мясистая область, тем меньше вероятность того, что она будет болезненной)
- тип процедуры (проколы кожи считаются менее болезненными)
- ваша индивидуальная переносимость боли
- уровень опыта и репутация вашего мастера по пирсингу
Хотя кожный пирсинг популярен и очень универсален, он также сопряжен с высоким риском осложнений.
Обязательно заранее обсудите следующие риски со специалистом по пирсингу:
- Инфекция. Если пирсинг не сделан в стерильной среде или уход за ним не осуществляется, бактерии могут проникнуть глубоко в дерму.
- Смещение. Если анкер вставлен недостаточно глубоко, он может сместиться в дерме и переместиться на другой участок кожи.
- Отказ. Отторжение происходит, когда кожные ткани разрастаются в дерме до полного вытеснения украшения. Хотя это обычное явление при смещении якоря, ваше тело может просто зарегистрировать его как нежелательный инородный объект и отвергнуть его.
- Повреждение тканей. Если анкер вставлен слишком глубоко, он может повредить окружающие кровеносные сосуды или нервы.
- Гипергрануляция. Отмечается красной шишкой вокруг места прокола. Гипергрануляция возникает, когда украшение слишком тугое или если место прокола раздражено каким-либо иным образом. Покрытие окружающей кожи косметикой или плотной тканью, постоянное обращение с украшениями и неправильная чистка могут привести к гипергрануляции.
- Рубцы. Если вы испытываете отторжение или иным образом отказываетесь от пирсинга, после заживления отверстия образуется небольшой шрам.
Покрытие окружающей кожи косметикой или плотной тканью, постоянное обращение с украшениями и неправильная чистка могут привести к гипергрануляции.Кожный пирсинг обычно заживает в течение одного-трех месяцев. Если вы не будете следовать рекомендациям мастера по последующему уходу, заживление пирсинга может занять больше времени.
Появление корки вокруг верхней части украшения и небольшой отек типичны в течение первых двух недель. Эти симптомы будут постепенно уменьшаться по мере продолжения процесса заживления.
Обычно они не вызывают беспокойства, если только из пирсинга не выделяется желтый или зеленый гной, он горячий на ощупь или не проявляются другие признаки инфекции.
Правильная очистка и уход имеют решающее значение для успеха вашего кожного пирсинга.
Во время заживления do :
- Держите пораженный участок повязкой в течение нескольких дней.
- Вымойте руки с антибактериальным мылом, прежде чем прикасаться к этой области.
- Используйте новое бумажное полотенце каждый раз, когда чистите пирсинг.
- Очищайте два раза в день морской солью или физиологическим раствором.
- Аккуратно сотрите корку, образовавшуюся между чистками.
- Накройте пирсинг, чтобы защитить его от намокания во время душа, если это возможно.
- Насухо промокните область после каждого очищения или после принятия душа.
В то же время, нельзя :
- Носите тесную одежду вокруг прокола.
- Пусть ваши волосы запутаются в украшениях.
- Занимайтесь спортом с высокой ударной нагрузкой или занимайтесь другими видами деятельности, где возможно столкновение.
- Погрузите проколотую область в ванну, бассейн или другой водоем.
- Используйте антисептики или антибактериальное мыло для очистки пирсинга.
- Протрите кожу полотенцем. Вместо этого промокните насухо.
- Удалите всю корку, которая образуется вокруг пирсинга.
- Меняйте украшение не менее чем на три месяца или пока пирсинг не заживет.
- Поиграйте с украшением или снимите его.
В то время как легкая припухлость и корочка являются нормальными для любого нового пирсинга, другие симптомы могут указывать на более серьезные проблемы со здоровьем.
Обратитесь к специалисту по пирсингу, если у вас возникнут какие-либо из следующих признаков инфекции или отторжения:
- Сильная боль
- тяжелая отек
- Кожа, которая горячая до прикосновения
- Желтый или зеленый разряд
- Фоловый запах
- Расш
С повторным.
Произойдет ли это в течение следующих трех месяцев или трех лет, зависит от того, насколько хорошо вы ухаживаете за пирсингом.После того, как кожный пирсинг полностью заживет (примерно через три месяца), вы сможете сменить внешнее украшение. Лучше всего, чтобы это сделал ваш мастер, чтобы избежать осложнений, таких как случайное смещение якоря.
Если вы все же решите заменить украшение самостоятельно, тщательно выполните следующие действия:
- Вымойте руки с антибактериальным мылом, прежде чем прикасаться к этой области.
- Очистите область морской солью или физиологическим раствором.
- Насухо промокните область.
- Отвинтите имеющуюся верхнюю часть украшения против часовой стрелки. Если верхняя часть упряма, вам, возможно, придется увидеть своего мастера по пирсингу. Мастер по пирсингу может использовать щипцы, чтобы отвинтить украшения.
- Привинтите новую верхнюю часть украшения по часовой стрелке.
- Еще раз очистите область и тщательно высушите.
Если вам нужно отказаться от кожного пирсинга, обратитесь к специалисту по пирсингу для профессионального удаления. Вы никогда не должны пытаться удалить этот тип пирсинга самостоятельно.
Ваш специалист по пирсингу, скорее всего:
- Очистите область стерильным раствором и промокните ее насухо.
- Отвинтите верхнюю часть украшений.
- Помассируйте кожу вокруг, чтобы помочь сместить якорь.
- С помощью скальпеля сделайте небольшой надрез по размеру основания анкера.
- С помощью скальпеля удалите рубцовую ткань, образовавшуюся вокруг фиксатора.
- С помощью пинцета вытащите анкер из кожи.
- Наложите шов или повязку на пораженный участок.
Несмотря на то, что врач общей практики или косметический хирург может удалить кожный покров, вам следует поговорить со специалистом по пирсингу, прежде чем приступать к удалению. Они могут обсудить плюсы и минусы того, чтобы сторонняя сторона удалила якорь, и, возможно, смогут дать направление, если это необходимо.
Потенциальный мастер по пирсингу из уважаемого магазина — ваш авторитет в вопросах кожного пирсинга. Они также могут ответить на конкретные вопросы, связанные с вашим желаемым размещением и связанными с этим рисками. Уважаемый мастер пирсинга также будет честен в отношении того, подходит ли желаемая область для кожного пирсинга.
прокол – определение и значение
- Дайте определение
- Связать
- Список
- Обсудить
- См.
- Услышать
- и Любовь
Определения
из Словаря английского языка American Heritage®, 5-е издание.
- непереходный глагол Проколоть острым предметом.
- непереходный глагол Сделать (дырку) прокалыванием.
- непереходный глагол Обесценивать или выкачивать.
- непереходный глагол Подлежит прокалыванию или прокалыванию.
- сущ. Действие или случай прокалывания.
- сущ. Отверстие или углубление, сделанное острым предметом, особенно отверстие в автомобильной шине.
из словаря века.
- сущ. Действие перфорации или укола остроконечным инструментом или проделывание им небольшого отверстия; небольшая рана, сделанная иглой, уколом или жалом: например, прокол ланцета, гвоздя или булавки.
- сущ. В зоология , вдавленная точка или точка, как бы проколотая; небольшое углубление, как бы уколотое в поверхность; пунктум. См. срез под Coscinoptera.
- Для укола; проткнуть острым концом любого вида: как, проколоть кожу.
из версии GNU Collaborative International Dictionary of English.
- переходный глагол Прокалывать маленьким остроконечным инструментом и т. п.; колоть; сделать прокол.
- сущ. Акт прокалывания; протыкая чем-то заостренным.
- сущ. Небольшое отверстие, сделанное острием; легкая рана, укус или жало.
п.; колоть; сделать прокол.- сущ. Акт или случай прокалывания.
- сущ. Отверстие, порез или разрыв, созданный острым предметом.
- глагол Проколоть; прорваться; прорвать дырку.
из WordNet 3.0 Copyright 2006 Принстонского университета. Все права защищены.
- глагол сделать прокалыванием
- сущ. потеря давления воздуха в шине при пробивании ее острым предметом
- глагол вызвать потерю давления воздуха или разрушение путем прокалывания
- сущ. маленькое отверстие, сделанное острым предметом
- глагол уменьшить или уменьшить размер или важность
- сущ. акт прокалывания или перфорации
- глагол быть проколотым или проколотым
- глагол протыкать острым предметом; сделать отверстие в
маленькое отверстие, сделанное острым предметомEtymologies
из Словаря английского языка American Heritage®, 4-е издание
[от среднеанглийского — a pricking, от позднелатинского pūnctūra , от pūnctus , prickus , до prick 4re 933 — причастие ; см. peuk- в индоевропейских корнях.]
Служба поддержки
Помогите поддержать Wordnik (и сделайте эту страницу свободной от рекламы), приняв слово «прокол».
Примеры
AngioDynamics сообщила в отчете FDA, что такой прокол является «возможным осложнением» любой такой операции.
