Улле неудачник: Недопустимое название | Ведьмак Вики

Содержание

как победить Улле Неудачника все способы

Содержание

Проклятая арена
Изгнание Улле
Чеканная монета
Видео прохождение

В Ведьмаке 3 «Мастер арены» это второстепенный квест, который можно получить просто путешествуя по острову Спикероог или в процессе прохождения цепочки квестов, посвященных кулачным боям.

Его обязательно нужно выполнить, чтобы получить доступ к финальному заданию: “Кулаки ярости: Чемпион Чемпионов”.

Так или иначе, вы попадаете в деревушку Хов, которая славится своей ареной, где лучшие бойцы не только Скеллиге, но и Северных Королевств, встречаются, чтобы сразиться за звание Чемпиона Чемпионов.

Проклятая арена

Возле арены двое распорядителей, воины Гуннар и Лидрик, хватаются за головы в отчаянии, так как судьба состязаний висит на волоске из-за духа проклятого Улле-Неудачника, островитянина, который по легенде при жизни никогда не побеждал в боях.

В своей последней схватке, которая по жеребьевке состоялась с ярлом Тормаром, Улле убил противника ножом, ударив в спину, за насмешки над собой. Умирающий ярл проклял неудачника на вечные проигрыши даже после смерти. Привычный к духам и проклятиям ведьмак, принимает заказ.

Изгнание Улле

В начале прохождения задания “Мастер арены” в Ведьмаке 3 измотанный вечными поражениями Улле, устало попросит Геральта «прикончить» его без лишнего пафоса. Но это окажется не так просто сделать.

Если попытаетесь просто убить Духа Арены, это ничего не даст, так как через день бедняга вернется на прежнее место.

Как же нам победить того, чье проклятье быть вечным проигравшим? Чтобы отправить Улле-Неудачника на тот свет в Ведьмаке 3, дайте горемычному духу победить вас. Умирать и подставляться под удары при этом не обязательно. Можно либо:

Пропустить несколько ударов и боги простят Улле, наконец-то призвав его на пир героев.
Парировать его удары. После восьмого блока Геральт победит Духа Арены, обойдясь без получения урона.

Чеканная монета

Обратите внимание, что квест “Мастер Арены” в Ведьмаке 3 завершается не после отправки призрака на тот свет и отчета перед заказчиком, а после получения обещанной награды. Гуннар и Лидрик обещали Геральту не только фиксированную награду, но и процент с первых боев, если тот изгонит духа.

Дополнительную награду в виде опыта и денег можно будет получить, только если поговорить с нанимателями снова после первой (неудачной) попытки победить Улле-Неудачника.

Чтобы закрыть квест, простая медитация на месте не поможет, необходимо покинуть не только Спикероог, но и в целом локацию Скеллиге. Достаточно, к примеру, отправится в Велен, а затем назад, тогда активируется диалог с воинами, которые и отдадут обещанные Белому Волку кроны.

Видео прохождение

Дикая Охота • FAQusha.RU [Вики]

Содержание прохождения:

org/ListItem»> Шаг 1: Поговорить с жителями деревни Хов
Шаг 2: Найти способ отправить Улле на тот свет

Дополнительное задание «Мастер арены» относится к скрытым заданиям и отмечается на карте желтым восклицательным знаком, который появляется на близком расстоянии от цели. С ареной на Спикерооге также связан финальный поединок в кулачных боях за звание чемпиона чемпионов.

Шаг 1: Поговорить с жителями деревни Хов

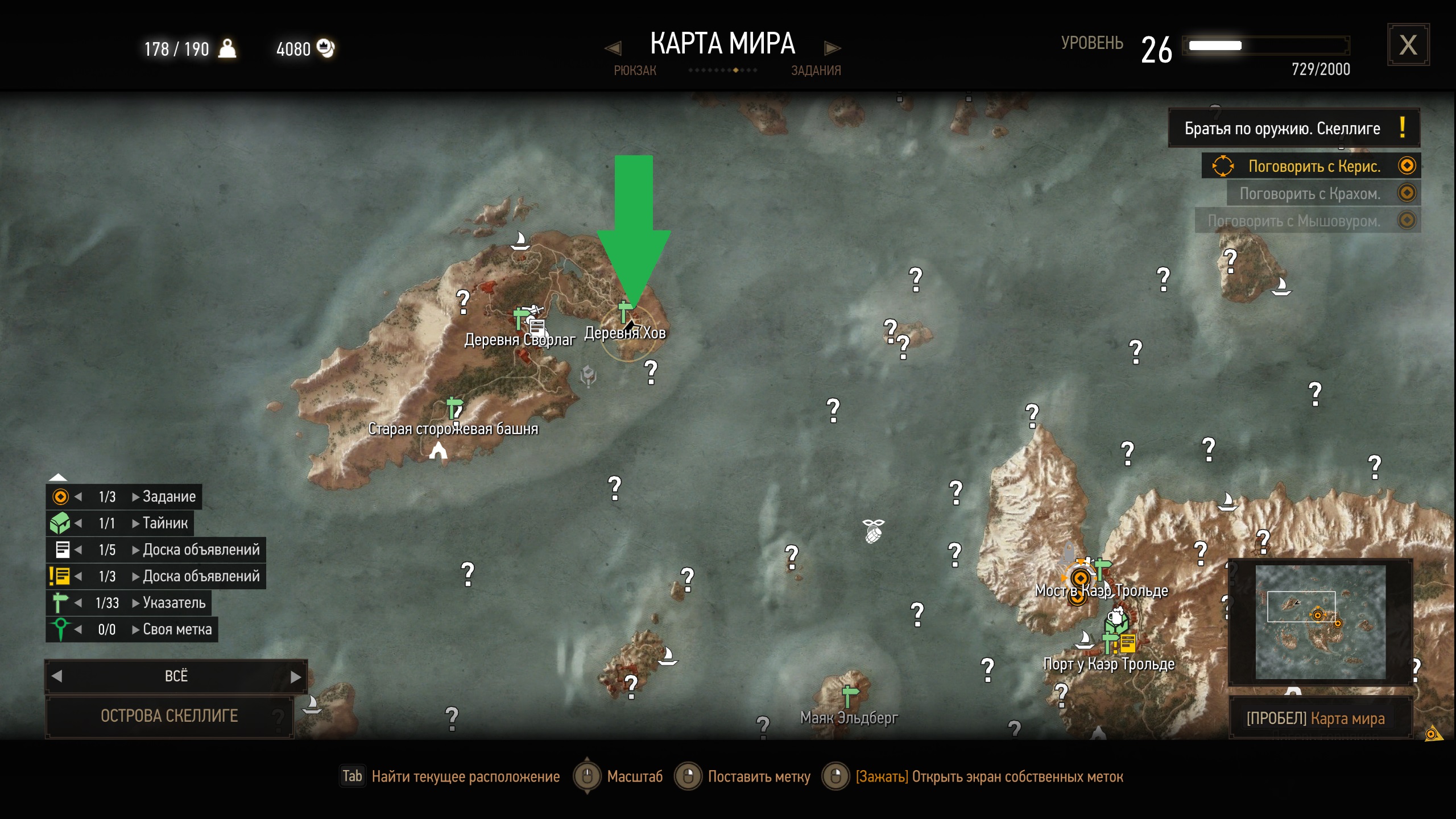
Улле Неудачник появляется на бойцовской арене в деревне Хов на восточном побережье острова Спикероог, куда Геральт приезжает на помощь Керис в дополнительно задании «Избранник богов». Если не рваться на арену, а сначала поговорить с Гуннаром и Лидриком на смотровой вышке, то бравые солдаты расскажут ведьмаку о частых появлениях призрака. Согласно легенде несколько поколений назад на арене выступал Улле Неудачник, который всегда проигрывал поединки, но быстро оправлялся от ран и постоянно возвращался на арену за очередной порцией унижения. Однажды на Спикерооге проводился большой турнир. Жребий свел ярла Тормара с Улле Неудачником.

Ярл на протяжении всего поединка издевался над своим противником и высмеивал на глазах у ревущей от восторга публики. Но веселье длилось недолго, разозленный Уве Неудачник пронзил обидчика ножом в спину, когда тот победно вскинул руки над головой. Перед смертью ярл Тормар проклял Уве Неудачника и пожелал тому проигрывать во веки веков. С тех времен на арене стал появляться бессмертный призрак, который до сих пор мешает проведению бойцовских состязаний. Призрака невозможно ни прогнать ни убить. В качестве награды за услугу Гуннар и Лидрик предложат ведьмаку процент от своих заработков, главное сейчас — прогнать духа.

к содержанию ↑

Шаг 2: Найти способ отправить Улле на тот свет

Закончив беседу, выходим на арену и дожидаемся появления духа. Улле Неудачник поприветствует очередного соперника и предложит сразиться. Хотя бесконечные поединки давно утомили призрака, он не может покинуть арену из-за проклятия. После каждого поражения он заново появляется на арене и издевательства повторяются вновь. Единственный способ отправить Улле Неудачника на тот свет — проиграть поединок, не сопротивляясь и не парируя ответных ударов. Если постоянно побеждать Улле Неудачника, то призрак продолжит появляться на арене. Когда Дух Арены покинет поле вечной битвы и отправится на пир героев, возвращаемся к Гуннару и Лидрику с благими вестями, а через пару дней забираем скромный процент от выигрышей на арене, которая быстро наполнится новыми гладиаторами. Для ускорения времени используем медитацию (клавиша [N]).

доп. задание

Владыка Ундвика, Избранник богов, Королевский гамбит, Очень ценный рог, Нитинг, Неоплаченный долг, Цена чести, Родовой меч, Шоковая терапия, Грустная история братьев Гроссбарт, Кредит доверия, Гвинт: игры по-скеллигски, Упражнения в высшей алхимии

Еще раз о правиле Борда и парном большинстве проигравших

Автор

В списке:

Нориаки Окамото
(Университет Кэйо)
Тойота Сакаи
(Университет Кэйо)

Зарегистрировано:

Тойота Сакаи

Abstract

Жан-Шарль де Борда ввел правило Борда с целью избежать так называемого парного большинства-проигравшего. Мы вернемся к этой теме, исследуя уникальность правила Борда как правила подсчета очков, которое согласуется с критерием попарного большинства-проигравшего. Сначала покажем, что эта единственность не выполняется ни для какой фиксированной совокупности. Фактически, когда есть три альтернативы и шесть избирателей, все правила подсчета очков согласуются с критерием попарного большинства-проигравшего. Затем мы показываем, что для каждого правила подсчета очков, отличного от правила Борда, существует совокупность n такая, что правило не согласуется с этим критерием для всех совокупностей размера, превышающего n.

Предлагаемая ссылка

Нориаки Окамото и Тойота Сакаи, 2019. » Еще раз о правиле Борда и парном большинстве проигравших ,» Обзор экономического дизайна, Springer; Society for Economic Design, vol. 23(1), страницы 75-89, июнь.

Обработчик: RePEc:spr:reecde:v:23:y:2019:i:1:d:10.1007_s10058-019-00221-3
DOI: 10.1007/s10058-019-00221-3

как

HTMLHTML с абстрактным простым текстом обычный текст с абстрактнымBibTeXRIS (EndNote, RefMan, ProCite)ReDIFJSON

Скачать полный текст от издателя

URL файла: http://link.

springer.com/10.1007/s10058-019-00221-3
Функция файла: Abstract
Ограничение на загрузку: Доступ к полному тексту статей этой серии ограничен .

URL-адрес файла: https://libkey.io/10.1007/s10058-019-00221-3?utm_source=ideas
Ссылка LibKey : если доступ ограничен и если ваша библиотека использует эту службу, LibKey перенаправит вас туда, где вы можете использовать свою библиотечную подписку для доступа к этому элементу
—>

Поскольку доступ к этому документу ограничен, вы можете поискать другую его версию.

Каталожные номера указаны в IDEAS

как

HTMLHTML с абстрактным простым текстомпростой текст с абстрактнымBibTeXRIS (EndNote, RefMan, ProCite)ReDIFJSON

Саари, Дональд Г., 1989 г. « Словарь парадоксов голосования «, Журнал экономической теории, Elsevier, vol. 48(2), страницы 443-475, август.
Паттанаик, Прасанта К., 2002 г. Позиционные правила коллективного принятия решений ,» Справочник по социальному выбору и благополучию, в: К. Дж. Эрроу, А. К. Сен и К. Судзумура (ред.), Справочник по социальному выбору и благополучию, издание 1, том 1, глава 7, страницы 361–394, Эльзевир.
Саари, Дональд Г., 2008 г. « Избавление от диктаторов, демистификация парадоксов голосования », Кембриджские книги, Издательство Кембриджского университета, номер 9780521731607, декабрь.
Уильям В. Герлейн, 2006 г.
Парадокс Кондорсе ,» Библиотека теории и решений C, Springer, номер 978-3-540-33799-7, декабрь.
Дональд Саари, 2006 г. « Что лучше: победитель Кондорсе или Борда? ,» Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, том. 26(1), страницы 107-129, январь.
Саари, Дональд Г., 1999 г. « Объяснение всех трех альтернативных результатов голосования «, Журнал экономической теории, Elsevier, vol. 87(2), страницы 313-355, август.
Фишберн, Питер С., 1974. « парадоксов голосования », Обзор американской политической науки, издательство Кембриджского университета, том. 68(2), страницы 537-546, июнь.
Смит, Джон Х., 1973 г. « Агрегация предпочтений с переменным электоратом «, Эконометрика, Эконометрическое общество, том. 41(6), страницы 1027-1041, ноябрь.

Саари, Дональд Г., 2008 г. « Избавление от диктаторов, демистификация парадоксов голосования », Кембриджские книги, Издательство Кембриджского университета, номер 9780521516051, декабрь.
К. Дж. Эрроу, А. К. Сен и К. Судзумура (ред.), 2002 г. « Справочник по социальному выбору и благосостоянию », Справочник по социальному выбору и благосостоянию, Эльзевир, издание 1, том 1, номер 1.

Полные ссылки (включая те, которые не соответствуют элементам в IDEAS)

Цитаты

Цитаты извлекаются проектом CitEc, подпишитесь на его RSS-канал для этого элемента.

как

HTMLHTML с абстрактным простым текстом обычный текст с абстрактнымBibTeXRIS (EndNote, RefMan, ProCite)ReDIFJSON

Процитировано:

Михоко Симамото, 2023. » Нормативное корпоративный подоходный налог с рентой для финансирования ЦУР: пример США
«, Устойчивое развитие, MDPI, vol. 15(4), страницы 1-18, февраль.

Наиболее похожие товары

Это элементы, которые чаще всего цитируют те же работы, что и этот, и цитируются теми же работами, что и этот.

Мостафа Дисс и Абдельмонаим Тлиди, 2018 г. Другой взгляд на парадокс Борда ,» Теория и решение, Springer, vol. 84(1), страницы 99-121, январь.
- Мостафа Дисс и Абдельмонаим Тлиди, 2016 г. « Другой взгляд на парадокс Борда ,» Рабочие бумаги 1632 г., Groupe d’Analyse et de Théorie Economique Lyon St-Etienne (GATE Lyon St-Etienne), Лионский университет.
- Мостафа Дисс и Абдельмонаим Тлиди, 2018 г. « Другой взгляд на парадокс Борда ,» Пост-печать halshs-01660816, HAL.
- Мостафа Дисс и Абдельмонаим Тлиди, 2017 г. Другой взгляд на парадокс Борда ,» Пост-печать halshs-01660828, HAL.
- Мостафа Дисс и Абдельмонаим Тлиди, 2016 г.
  
  « Другой взгляд на парадокс Борда ,» Рабочие бумаги halshs-01402268, HAL.
Саари, Дональд Г. и Макинти, Томас Дж., 2013 г. » Соединение парных и позиционных результатов выборов ,» Математические социальные науки, Elsevier, vol. 66(2), страницы 140-151.
Ли Гибсон и Роберт Пауэрс, 2012 г. Расширение теоремы МакГарви с точки зрения механизма множественного коллективного выбора ,» Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, том. 38(1), страницы 101-108, январь.
Мухаммад Махаджне, Шмуэль Ницан и Оскар Волидж, 2015 г. « Консенсус уровня $$r$$r и стабильный социальный выбор ,» Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, том. 45(4), страницы 805-817, декабрь.
Винсент Мерлин и Ипек Озкал Санвер и М. Ремзи Санвер, 2019 г.. «
Пересмотр правил компрометации «, Групповое решение и переговоры, Springer, vol. 28(1), страницы 63-78, февраль.
- Винсент Мерлин и Ипек Озкал Санвер и М. Ремзи Санвер, 2019. « Пересмотр правил компрометации «, Пост-печать halshs-02065282, HAL.
Мухаммад Махаджне, Шмуэль Ницан и Оскар Волидж, 2013 г. « УРОВЕНЬ r СОГЛАСИЯ И СТАБИЛЬНОГО СОЦИАЛЬНОГО ВЫБОРА ,» Рабочие бумаги 1305 г., Университет Бен-Гуриона в Негеве, факультет экономики.
- Мухаммад Махаджне, Шмуэль Ницан и Оскар Волидж, 2014 г. « Консенсус уровня r и стабильный социальный выбор », Серия рабочих документов CESifo 4808, CESifo.
Уэсли Х. Холлидей, Чейз Норман, Эрик Пакуит и Саам Захедиан, 2022 г. « Теоремы невозможности, связанные с ослаблением последовательности расширения и решительности в голосовании ,» Документы 2208.06907, arXiv.org, пересмотрено в марте 2023 г.
Уэсли Х. Холлидей и Эрик Пакуит, 2020 г. Цикл разделения: новый последовательный метод голосования по Кондорсе, независимый от клонов и невосприимчивый к спойлерам ,» Документы 2004. 02350, arXiv.org, пересмотрено в марте 2023 г.
Дональд Саари, 2010 г. « Систематический анализ множественных правил голосования ,» Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, том. 34(2), страницы 217-247, февраль.
Луис Г. Варгас, 2016 г. « Голосование с интенсивностью предпочтений «, Международный журнал информационных технологий и принятия решений (IJITDM), World Scientific Publishing Co. Pte. ООО, вып. 15(04), стр. 839-859, июль.
М. Санвер и Уильям Цвикер, 2009 г. » Односторонняя монотонность как форма устойчивости к стратегии
,» Международный журнал теории игр, Springer; Game Theory Society, vol. 38(4), страницы 553-574, ноябрь.
Эяль Бахарад и Шмуэль Ницан, 2016 г. » Возможна ли согласованность большинства? ,» Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, том. 46(2), страницы 287-299, февраль.
Саари, Дональд Г. , 2014 г. Объединение теории голосования от теорем Накамуры до теорем Гринберга ,» Математические социальные науки, Elsevier, vol. 69(С), страницы 1-11.
Макинти, Томас Дж. и Саари, Дональд Г., 2017 г. » Вероятность результатов голосования с обобщенными вероятностями IAC ,» Математические социальные науки, Elsevier, vol. 87(С), страницы 1-10.
Рауль Перес-Фернандес и Бернар Де Баэтс, 2018 г. Отношение суперпокрытия, попарный победитель и другие недостающие звенья между Борда и Кондорсе ,» Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, том. 50(2), страницы 329-352, февраль.
Терзопулу, Зои и Эндрисс, Улле, 2021. « Борда класса «, Журнал математической экономики, Elsevier, vol. 92(С), страницы 31-40.
Ву-Сюн Хуан, 2014 г. « Сингулярность и парадокс Стрелы «, Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, том. 42(3), страницы 671-706, март.
Уэсли Х. Холлидей и Эрик Пакуит, 2020 г. Решающие коалиции Стрелы ,» Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, том. 54(2), страницы 463-505, март.
Аки Лехтинен, 2007 г. « Правило Борда также предназначено для нечестных людей ,» Общественный выбор, Springer, vol. 133(1), страницы 73-90, октябрь.
Себастьен Куртен, Бонифаций Мбих и Иссофа Мойуу, 2014 г. « Так ли плохи процедуры Кондорсе согласно аксиоме подкрепления? ,» Социальный выбор и благосостояние, Springer; Общество социального выбора и благосостояния, том. 42(4), стр. 927-940, апрель.
- Себастьен Куртен, Бонифаций Мбих и Иссофа Мойуу, 2012 г. « Так ли плохи процедуры Кондорсе согласно аксиоме подкрепления? ,» Рабочие документы ТЕМА 2012-37, THEMA (Экономическая теория, моделирование и приложения), Университет Сержи-Понтуаз.
- Себастьен Куртен, Бонифаций Мбих и Иссофа Мойуу, 2014 г. « Так ли плохи процедуры Кондорсе согласно аксиоме подкрепления? ,» Пост-печать hal-00914870, HAL.

Подробнее об этом изделии

Ключевые слова

Правило Борда; Социальный выбор; Парное большинство-проигравший; Правило подсчета очков; критерий Кондорсе;
Все эти ключевые слова.

Статистика

Доступ и статистика загрузки

Исправления

Все материалы на этом сайте предоставлены соответствующими издателями и авторами. Вы можете помочь исправить ошибки и упущения. При запросе исправления, пожалуйста, укажите дескриптор этого элемента: RePEc:spr:reecde:v:23:y:2019:i:1:d:10.1007_s10058-019-00221-3 . См. общую информацию о том, как исправить материал в RePEc.

По техническим вопросам, касающимся этого элемента, или для исправления его авторов, названия, реферата, библиографической информации или информации для загрузки, обращайтесь: . Общие контактные данные провайдера: http://www.springer.com .

Если вы создали этот элемент и еще не зарегистрированы в RePEc, мы рекомендуем вам сделать это здесь. Это позволяет связать ваш профиль с этим элементом. Это также позволяет вам принимать потенциальные ссылки на этот элемент, в отношении которых мы не уверены.

Если CitEc распознал библиографическую ссылку, но не связал с ней элемент в RePEc, вы можете помочь с помощью этой формы .

Если вы знаете об отсутствующих элементах, ссылающихся на этот, вы можете помочь нам создать эти ссылки, добавив соответствующие ссылки таким же образом, как указано выше, для каждого ссылающегося элемента. Если вы являетесь зарегистрированным автором этого элемента, вы также можете проверить вкладку «Цитаты» в своем профиле RePEc Author Service, так как некоторые цитаты могут ожидать подтверждения.

По техническим вопросам относительно этого элемента или для исправления его авторов, названия, реферата, библиографической информации или информации для загрузки обращайтесь: Sonal Shukla или Springer Nature Abstracting and Indexing (адрес электронной почты доступен ниже). Общие контактные данные провайдера: http://www.springer.com .

Обратите внимание, что фильтрация исправлений может занять пару недель. различные услуги RePEc.

Фонд T. Rowe Price Emerging Europe

1 место из 13 в — Разное Регион более 0 месяцев Все расчеты производятся в долларах США, если не указано иное.

Citywire отслеживает эффективность карьеры всех портфельных менеджеров. Рейтинги и полные данные об эффективности показаны только для лицензированных фондовых групп. Узнайте больше здесь. Управляющим активами, заинтересованным в лицензировании Citywire Portfolio Manager Ratings, следует обращаться по адресу [email protected]

. Цель

Инвестиции нацелены на долгосрочный прирост капитала за счет инвестиций в основном в обыкновенные акции компаний, расположенных (или осуществляющих основную деятельность) в странах Европы с формирующимся рынком. Фонд обычно инвестирует не менее 80% своих чистых активов (включая любые займы для инвестиционных целей) в развивающиеся рынки Европы, включая Восточную Европу и бывший Советский Союз. Он может покупать акции компаний любого размера. Фонд не диверсифицирован.

Управляется:

Улле Адамсон

Улле Адамсон является управляющим портфелем фонда Emerging Europe Equity в подразделении акций компании T. Rowe Price. Она является вице-президентом и членом инвестиционного консультативного комитета фонда T. Rowe Price Media & Tele Communications. Она также является держателем сертификата CFA.

Пожалуйста, ознакомьтесь с условиями и положениями об ограничениях на использование базы данных Citywire Portfolio Manager.

Производительность

Разное Регион

Над 10 лет 5 лет 3 года 2 года 1 год 3 месяца 1 месяц

30. 04.2022 — 30.04.2023

Общий доход

Месяц за месяцем Производительность

Квартальная производительность

по 31.03.2023	Годовой	Q1	Q2	Q3	Q4
2023		17,5%
2022	-83,7%	-83,2%	-19,1%	-7,1%	29,5%
2021	14,6%	1,2%	14,5%	8%	-8,5%
2020	-8,3%	-37,3%	23,4%	-5%	24,9%
2019	30,9%	9,5%	9,5%	-4,2%	14%
2018	-14,4%	6,2%	-12,3%	0,1%	-8,2%
2017	19,7%	1,4%	3,4%	11,6%	2,4%
2016	21,5%	8,9%	-1,7%	7,8%	5,3%
2015	-10,1%	-0,8%	3,1%	-13,3%	1,5%
2014	-35,8%	-14,2%	10%	-13,2%	-21,6%
2013	4%	0,4%	-5,5%	6,7%	2,8%
2012	25,2%	20,6%	-10,4%	9,2%	6,1%
2011	-33,2%	3%	-4,7%	-31%	-1,4%
2010	33,5%	11,7%	-13,2%	19,8%	14,9%
2009 г.	125,1%	-1,9%	58,8%	30,6%	10,7%
2008 г.	-75,9%	-11,2%	5,5%	-42,7%	-55%
2007 г.	27,9%	1,5%	5,9%	4,6%	13,7%
2006 г.	34,7%	11,6%	-9,1%	12,9%	17,6%
2005 г.	59%	10,8%	10,6%	23,6%	5%
2004 г.	30%	18,9%	-9,8%	3,4%	17,3%
2003 г.	69,2%	-3,6%	29,9%	14%	18,5%
2002 г.	3,7%	12,8%	-13%	-9,1%	16,2%
2001 г.	-7,7%	-22,1%	12,4%	-22,7%	36,3%
2000 г.					-17,3%

Доходность и риск

Распределение активов

Разбивка

31.

03.2023

Топ-10 холдингов

Акции	Размер
Национальный банк Греции SA	15,26%
Коч Холдинг АС	8,2%
ОТП Банк ПЛС	6,95%
Kaspi.kz АО ГДР	5,29%
АО «Народный сберегательный банк Казахстана» ГДР	4,78%
Бим Бирлесик Магазалар АС	4,73%
Евробанк Эргасиас Сервисез Энд Холдингс С. А.	4,6%
Powszechny Zaklad Ubezpieczen SA	4,26%
Обыкновенные акции Inpost SA	3,56%
Греческая организация Football Prognostics SA	3,22%

31.03.2023

Зарегистрировано для продажи в

США

долларов США

Информация о фонде
Дата запуска	31. 08.2000
Поделиться размером класса	32 Мн
Базисная валюта
В

Информация о покупке
Мин. первоначальные инвестиции	2500
Мин. регулярные дополнительные инвестиции	100

Сборы
Годовое управление	1,04%

Производительность указана за указанный период (с конца месяца до конца месяца, ставка/ставка, реинвестированный валовой доход, рассчитанный в указанной валюте и валютах).