Тетраэдр схема сборки: Тетраэдр из бумаги (4 схемы-инструкции)

Тетраэдр из бумаги (4 схемы-инструкции)

Главная » Геометрические фигуры

Просмотров 1.6k. Обновлено Июл 5, 2011

Выдали задание по геометрии и не знаете, как сделать тетраэдр из бумаги? Мы постараемся вам помочь в решении этой проблемы. Попробуем использовать простые приемы оригами, которые может освоить каждый.

Итак, чтобы собрать правильный тетраэдр из бумаги вам придется для начала выбрать один из нескольких способов, так как мы приготовили их несколько для вас. Давайте рассмотрим их по порядку!

Тетраэдр из бумаги схемы сборки

Первый вариант

Для сборки нам понадобится:

• 6 листков бумаги размерами 4 на 3.4 сантиметра (вы можете выбрать свой размер, сохраняя пропорции).
• 15 минут свободного времени.

Для начала мы собираем элементы, а потом скрепляем их вместе. Если конструкция плохо держится, то можно использовать клей (хотя и без него модель держится надежно).

Второй вариант

В этом варианте сборка бумажного тетраэдра будет происходить из единого, цельного листа бумаги, а именно полоски. За размер бумаги не переживайте, подойдет любой (A4 в развороте за глаза).

Третий вариант

Вот ещё одна схема, которая расскажет о том, как легко собирается бумажный тетраэдр. Тут вам понадобится один квадратный лист бумаги и пять минут свободного времени. На мой взгляд самая оптимальная и простая модель.

Четвертый вариант

Экзотический способ. Здесь мы будем собирать пустой тетраэдр из бумаги, который имеет только ребра и не имеет туловища. Для сборки понадобится 6 листков бумаги (3 на 9 см.)

То, что нам нужно, происходит с 0 по 5 минуту видеоролика.

• Автор: Сергей
• Распечатать

Оцените статью:

(5 голосов, среднее: 2 из 5)

Поделитесь с друзьями!

Jo Nakashima

• org/Comment» itemscope=»»>

  2014-09-28T17:31:01+00:00

  Мария Какурина

  Спасибо вам огромное!!!По геометрии задали сделать такую штуку!Третий вариант сделаю!Он круче и лучше!!!Огромное вам спасио!!!!Спасли!!!!!

• 2014-02-23T10:00:15+00:00

  AbstractSuper

  Третий вариант, насколько я понимаю, из книжки Оригами для знатоков — его независимо разработали Казуо Хага, Кунихико Касахара и Джан Маэкава

• 2014-02-23T00:49:23+00:00

  org/Person»> tamasya

  Давно хочу сделать.Очень нравиться.Буду пробовать.

• 2014-01-24T07:02:23+00:00

  Максим Ефимов

  любой размер

• 2012-03-28T20:55:17+00:00

  интересно.буду делать

• 2012-01-21T22:09:52+00:00

  НастюшкаА

  Класс)))Не знаете что за музыка?

Тетраэдр из бумаги или картона своими руками

Оригами-тетраэдр из бумаги – эффектный и многофункциональный декоративный элемент. В зависимости от модели, он может служить интерьерной подвеской, ёлочным украшением и частью модного настенного панно в скандинавском стиле. Тетраэдр – четырёхгранная пирамида, в основании которой лежит треугольник. Чаще всего для декора используют несколько таких фигур, объединённых в композицию.

Традиционный вариант

Объёмный тетраэдр-оригами можно сделать из классического квадрата или листа бумаги формата А4. Схема во втором варианте – сложнее, однако для долговечного декора лучше выбирать именно её. Модель получается многослойной, а потому меньше изнашивается в процессе эксплуатации.

Пошаговая инструкция:

Нам понадобится 2 альбомных листа. Складываем их поочерёдно по одному и тому же алгоритму.

1. Располагаем лист короткой стороной к себе. Намечаем вертикальную ось симметрии.
2. Правый нижний угол поднимаем к центральной линии из шага 1.
3. Переворачиваем заготовку.
4. Левый верхний угол опускаем, делая сгиб по линии, намеченной в шаге 2.
5. Вот что должно получиться.
6. Раскрываем изделие.
7. Повторяем шаги 2-5 с другой стороны.
8. Срезаем верхнюю часть по выделенной на схеме линии.

9. Складываем левый верхний угол по пунктиру. Его вершину совмещаем с точкой, указанной стрелкой.
10. Повторяем то же действие для правого нижнего угла.
11. Вот такая полоска-«конверт» должна получиться.
12. Повторяем шаги 1-10 для другого листа А4, но зеркально.
13. Кладём один модуль поверх другого, как показано на схеме.
14. Нижний элемент складываем в тетраэдр.
15. Оборачиваем верхнюю часть вокруг получившейся фигуры.
16. Вставляем оставшийся клапан в зазор, чтобы тетраэдр-оригами не распадался.

Эта модель великолепно смотрится в настенных панно:

Или мобильных подвесках:

Есть и немного другая схема сборки тетраэдра – из одного листа А4. Она представлена в видео-уроке:

Модель от Томоко Касахары

Японский оригамист предлагает сделать модель тетраэдра из квадратного листа. Схема сборки от Касахары настолько подробная, что изготовить по ней фигурку сможет даже начинающий. Для удобства рекомендуется использовать бумагу со сторонами разного цвета – это поможет следить за процессом складывания. Опытные мастера могут брать однотонные листы, что улучшит эстетические качества модели.

Пошаговая инструкция:

1. Начинаем с изнанки листа. Делим квадрат пополам путём складывания. Намечаем «засечку» и раскрываем сгиб. Правую половину тоже складываем вдвое. Наносим отметку примерно на полпути вверх. Разворачиваем лист до исходного состояния.
2. Делаем сгиб по пунктиру, ориентируясь на «засечки» из шага 1.
3. Повторяем аналогичное действие с противоположной стороны.
4. Опускаем верхний край на 1 см.
5. Подгибаем уголки по стрелкам.
6. Раскрываем все складки, кроме последних. Делим новый квадрат пополам по горизонтали.

7. Намечаем диагональные сладки в местах, указанных пунктиром.
8. Делаем короткие боковые сгибы по стрелкам. Важно каждый раз совмещать нижний край клапана с меткой по центру.
9. Предварительные сгибы нанесены, теперь можно переходить к складыванию объёмной фигуры. Нижний левый угол сгибаем по пунктирной линии до пересечения, указанного стрелкой.
10. Далее совмещаем его с вершиной треугольника.
11. Точку 1 опускаем до конца стрелки, а затем откидываем клапан 2, чтобы зафиксировать последний сгиб.
12.  Получившаяся фигура напоминает перевёрнутый рожок для мороженого. Нажимаем на складки в правой части модели, поднимаем точку 1 вверх, как показано на схеме, и «заправляем» под клапан. Тетраэдр-оригами почти готов, но у него остаётся одна лишняя грань. Чтобы завершить сборку, точку 2 перемещаем по стрелке и фиксируем клапаном.

Освоив схему сборки тетраэдра Касахары, можно также изготавливать из бумаги своими руками эффектные подарки – разнообразные панно и картины:

Альтернативный вариант сборки из квадрата:

Очень простая двухцветная модель

Необычно и эффектно смотрится тетраэдр из двух половинок. Каждую можно сложить из бумаги другого цвета, что сделает геометрический декор ещё интереснее. Если предыдущие модели адресованы, скорее, опытным мастерам, эта – как раз по плечу начинающим.

Пошаговая инструкция:

1. Сгибаем квадрат по диагонали «горой». Делим пополам, складывая слева направо и сверху вниз. Делаем складки и раскрываем.
2. Намечаем сгиб слева по пунктирной линии. Соединяем вершину угла с ближней засечкой.
3. Аналогичные сгибы делаем ещё с трёх сторон.
4. Все четыре края складываем по пунктирным линиям. Центральные треугольники выступают вверх, образуя так называемые «заячьи уши». Раскрываем их изнутри и сплющиваем.
5. Сгибаем фигуру пополам «долиной».

Аналогичным образом собираем вторую часть. Остаётся склеить двухцветный тетраэдр из бумаги и придумать ему применение.

Декор из картона

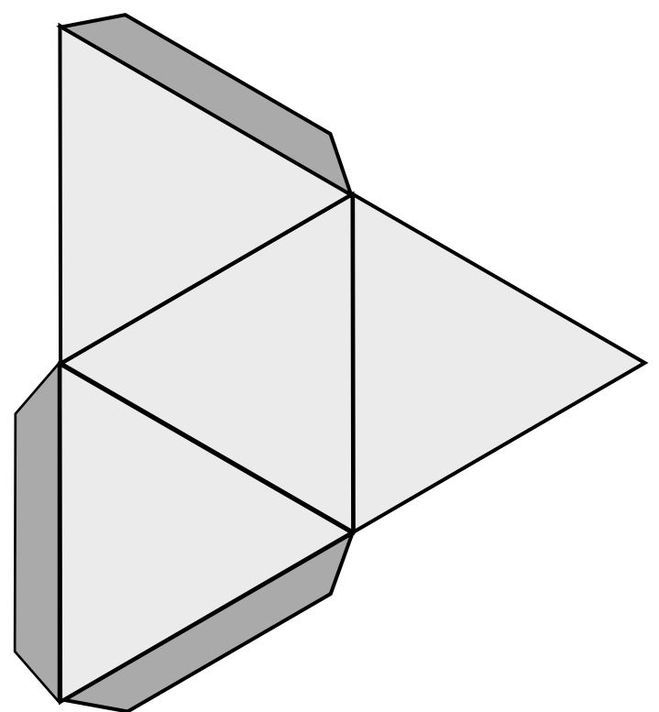
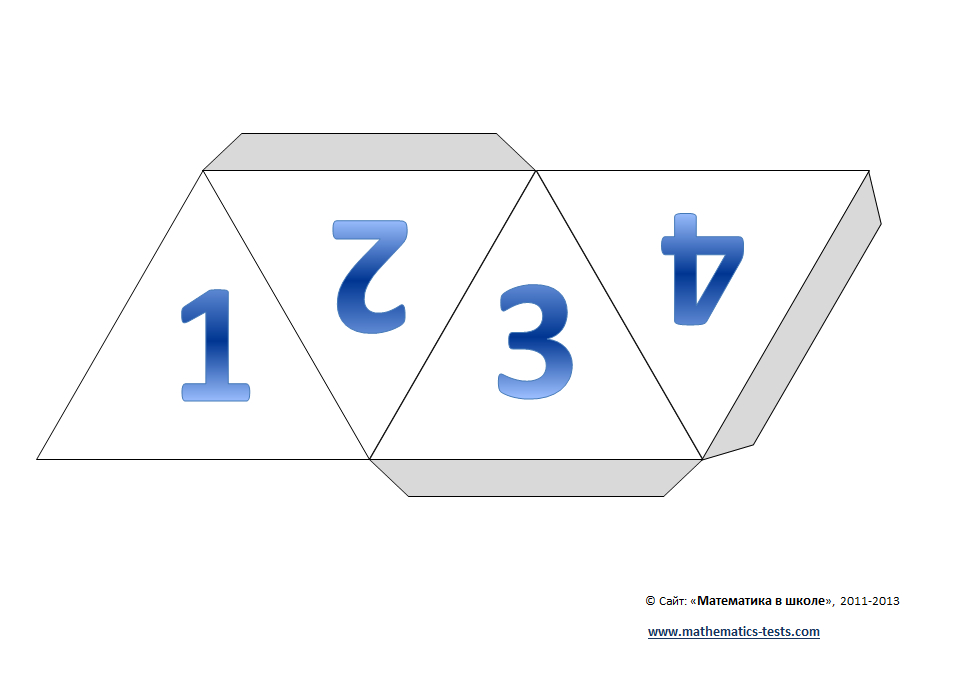
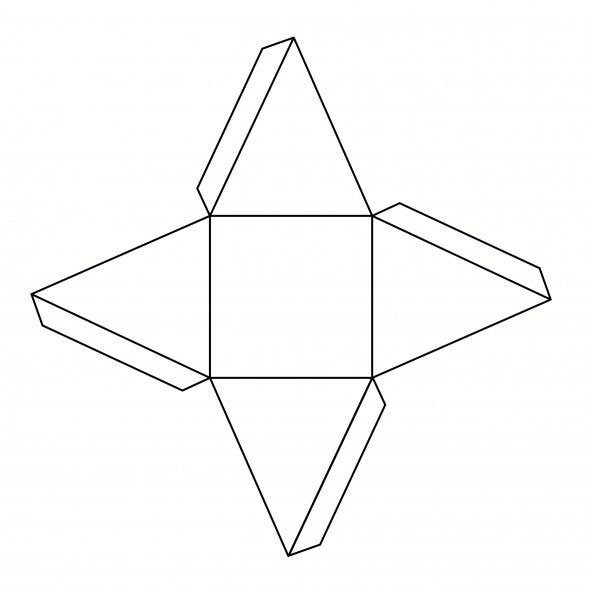
Рассматривая варианты оригами-тетраэдра, нельзя обойти вниманием фигуры, изготовленные другим способом, но не менее популярные. Речь идёт о картонных моделях, которые складываются из развёртки, как упаковочные коробочки. Скачиваем трафарет правильного тетраэдра:

Остаётся распечатать его на цветной картон и вырезать заготовки, а затем склеить:

Звёздчатый многогранник

Самая красивая модель получается из нескольких тетраэдров, соединённых между собой. Этот так называемый звёздчатый многогранник, легко сделать своими руками из картона. Тетраэдры собирают из отдельных граней – узких полосок, сложенных «уголком». Именно поэтому нужна не бумага, а плотный картон, иначе ажурная конструкция быстро сомнётся под собственным весом.

Число выступов декоративного кристалла может быть разным. Максимум можно использовать 5 взаимно пересекающихся тетраэдров. Их размер для схемы не важен, но соотношение сторон исходного листа должно составлять 1:3.

Пошаговая инструкция:

Для начала запасаемся листами тонкого дизайнерского картона. Для звезды диаметром 16,5 см нам понадобится 30 прямоугольников размером 5х15 см. Можно выбрать другие параметры, главное, сохранить указанные пропорции. Чтобы не запутаться, рекомендуем делать полосы партиями по 6 штук разного цвета.

1. Первую полосу сгибаем вдвое по высоте. Раскрываем складку.
2. Оба края сводим к середине.
3. Делаем складку-засечку «долиной».
4. Левый угол сгибаем, чтобы красная точка коснулась отметки из шага 3. Раскрываем.
5. С помощью обратной складки заводим левый угол внутрь.
6. Раскрываем правую сторону. «Прячем» выступающий уголок. И вновь закрываем правую половину.
7. Намечаем складку «долиной» с другой стороны.
8. Повторяем шаги 3-7 на противоположном конце полосы.

Таких заготовок понадобится 30 штук. На лицевой стороне делаем складку «долиной», а на обороте – «горой».

Начинаем сборку пирамидок. Для первой используем 6 красных элементов. Верхний угол намечаем небольшой бумажной полоской, чтобы в дальнейшем упростить себе работу.

Остальные грани собираем и склеиваем по 3 штуки. Тщательно проходим стыки, тогда конструкция получится прочной и долговечной.

К первому красному тетраэдру добавляем полуготовую фигуру из 3-х граней. Ориентируемся на фото-образец. Теперь фиксируем второй – жёлтый тетраэдр, приклеивая ещё 3 недостающие грани.

Аналогичным образом вставляем следующую заготовку, например, голубого цвета и закрепляем её.

Поворачиваем тетраэдр-звезду другой стороной и продолжаем работу.

Следим, чтобы каждая добавленная фигура располагалась под тем же углом, что и остальные.

Последний, фиолетовый, многоугольник крепим с особой тщательностью.

Прежде чем приклеить 3 завершающие грани, несколько раз осматриваем звезду под разными углами. Желательно добиться идеальной симметрии.

Казалось бы, сложная конструкция, на деле требует только аккуратности, внимания и терпения, как и остальные модульные многогранники.

Тетраэдр из картона послужит отличным украшением праздничного интерьера или, например, магазинной витрины.

А эксцентричные невесты вполне могут заменить им свадебный букет.

Звёздчатый многогранник – единственный способ сложить оригами-тетраэдр из модулей. Есть и не менее интересные варианты:

Интересные факты

Тетраэдр – одно из самых интересных, с точки зрения коммерции, платоновых тел. Достаточно простая пирамидка известна каждому с детства. В таких треугольных пакетах – тетропаках  во времена СССР продавали молоко, кефир и сливки. Считалось, что благодаря пирамидальной форме деликатная продукция дольше сохраняется свежей.

Треугольная упаковка – совсем не советское изобретение. В 1930-х годах французский научно-популярный журнал «Science & Vie» опубликовал статью о загадочных свойствах египетских пирамид, где тела фараонов не портились, а мумифицировались естественным путём. Теория не подкреплялась серьёзными доказательствами, однако шведский изобретатель Эрик Валленберг настолько увлёкся ею, что создал мини-аналог древнеегипетских усыпальниц – ту самую картонную упаковку Tetra Classic. Он хотел снизить потери молокоторговцев, но на деле оказал помощь производителям одноразовой тары. Его пирамидки выпускались быстро, в больших объёмах и практически без отходов.

В 1950 году на базе инновационной технологии была создана компания AB Tetra Pak. Однако, когда выяснилось, что продукция в картонных пирамидках скисает почти так же быстро, как в стеклянных бутылках, шведы утратили интерес к идее Валленберга. Тем не менее, технологию производства удалось продать советскому руководству, делая упор на её бюджетность и эффективность. Так на наших прилавках появились легендарные «треугольнички» с надписью «Молоко». Чтобы транспортировка пакетов-тетраэдров была не менее выгодной, чем производство, под них изготовили специальные шестиугольные контейнеры.

Сегодня трёхмерные треугольные пакеты (точнее, пакетики) взяла на вооружение компания Lipton. Производитель утверждает, что заменяет плоскую порционную упаковку объёмной, чтобы продемонстрировать красоту раскрывшегося в чашке чайного листа. И показать, что в пакетиках не обрезки и крошка, как подозревают потребители, а полноценный качественный купаж.

FIT (Пять пересекающихся тетраэдров) — Оригами Михала Космульского

Инструкции 3 декабря 2006 г. 18 апреля 2021 г.
http://origametry.net/fit.html
Детали модели: FIT (пять пересекающихся тетраэдров) (к: Том Халл)
Смотрите также: FIT (Пять пересекающихся тетраэдров) других цветов, FIT (Пять пересекающихся тетраэдров), серебристый
Типы моделей: модульный плетеный многогранник
Место расположения: на этой странице, на другом сайте
Тип: Пошаговая схема, Советы по складыванию

Инструкции по складыванию Тома Халла

Модель

«Пять пересекающихся тетраэдров» (FIT), разработанная Томасом Халлом, вероятно, является самой популярной моделью тип плетеного многогранника и интересный математический объект также.

Автор подготовил инструкции по складыванию, включая схемы складывания блоков и информацию по их сборке, на веб-страница модели. В то время как складывать блоки довольно просто, соединить их надлежащим образом — нет.

Мои советы по сборке модели

Оригинальная инструкция по сборке адекватна, но не идеальна. В этой статье я описываю некоторые правила и советы, которые я придумал при сборке этой модели, которая мы надеемся, что это может быть полезно и для других папок.

Если вам уже удалось один раз сложить модель, настоящая сложенная модель — лучшая помощь, которую вы можете получить, и намного лучше, чем любые плоские картинки или схемы. Если у вас нет под рукой сложенной модели, вы можете использовать изображения готовой модели, найденные здесь, в качестве справки. Последние несколько фото трехмерные анаглифные изображения, которые можно просматривать в красно-голубых очках, создавая впечатление трехмерности.

Перед тем, как вы приступите к чтению моих заметок, я также должен упомянуть еще один, очень интересный способ сборки. описан Дирком Эйснером и основан на идеях Роберт Дж. Ланг и Франческо Манчини. Этот метод полностью отличается от моего и начинается с создания трехмерного соединения четырех треугольников (не тетраэдров). Это, безусловно, стоит попробовать.

Предупреждение о спойлере : в моем случае, как только я пришел к правилам, описанным ниже, я смог довольно быстро закончить модель. рекомендую сначала попробовать все самостоятельно, следуя только советам, найденным на странице Тома Халла, и возвращайтесь к инструкциям ниже, только если вы не можете справиться. Узнать правила и глубокая симметрия этой модели действительно забавна, даже если для завершения модели требуется больше времени.

• Две общие раскраски для этой модели: либо использование пяти разных цветов, по одному для каждого тетраэдра, либо использование одного цвета. мне кажется монохром версия выглядит более элегантно, но если вы складываете FIT впервые, рекомендую начать с разноцветной версии. Разные цвета действительно помогают чтобы отслеживать различные кадры внутри запутанной модели и упростить поиск пути.
• Начните с двух фреймов, расположенных так, что вершина одного проходит через основание другого и наоборот («трехмерная звезда Давида»).

• Посмотрите прямо на вершину, проходящую через основание другого тетраэдра (например, вершину оранжевого тетраэдра, ближайшую к наблюдателю в третье изображение, показанное здесь).
• Теперь вам нужно сплести три других четырехгранных рамки вокруг основания, состоящего из двух рамок. Взгляните на высокую симметрию трех дополнительные тетраэдры. Одно ребро каждого из них проходит под одним из трех видимых ребер оранжевого тетраэдра. Два ребра каждого из этих тетраэдров «окружите» один край оранжевого тетраэдра, поместив этот край внутрь «вилки».
• Как только вам удастся добавить третий кадр (что, на мой взгляд, является самым сложным шагом), четвертый и пятый будут намного проще, потому что из-за высокой симметрии, можно просто скопировать третий кадр, только повернутый. Обратите внимание, что под ближайшей видимой вершиной оранжевого тетраэдра (и, симметрично, под любой другой вершина), три рамки разного цвета пересекаются, образуя треугольник, аналогичный внутренней части Кольца Борромео. Эта структура частично видна на последнем изображении под передней вершиной красной рамки.
  • В качестве альтернативы, после того, как вы собрали три тетраэдра, найдите «узел», где три ребра трех разных тетраэдров сплетены вместе, и попытайтесь поместите над ними сборку из трех частей. На третьем изображении справа это будет соответствовать соединению красной, светло-зеленой и темно-зеленой рамок, и глядя на них, пытаюсь разместить над ними три соединенных оранжевых элемента (а затем добавляя три других оранжевых элемента сзади, чтобы закрыть рамку).

3D анаглиф 3D анаглиф с отверстием 3D анаглиф с вершиной 3D анаглифный вид под углом

• Трехмерные анаглифные изображения этой модели могут оказаться весьма полезными, если вы запутались.
• Обратите внимание, что порядок, в котором цвета появляются на каждой из пятиугольных граней нижележащего додекаэдра, не одинаков для каждой грани.
  Так, например, на втором изображении такой порядок (по часовой стрелке): оранжевый, красный, темно-зеленый, светло-зеленый, желтый на лице видно спереди, но в некоторых местах он отличается других лиц.
• На странице Тома вы найдете подсказку, в которой говорится, что готовый объект имеет свойство переплетаться любых двух тетраэдров с торчащим одним углом отверстие другого и наоборот. Это верно и очень полезно наблюдать, но имейте в виду, что это необходимое условие, но не достаточное. Это означает, что можно начать переплетение рамок и сохранить вышеуказанное условие при создании промежуточной модели, которая не позволит вам чтобы добавить больше кадров и создать желаемую готовую модель. Например, если вы добавите третий кадр таким образом, что его одна и та же вершина будет проходить через две грани из двух других тетраэдров вы получите модель, которая соответствует критерию, описанному выше, но которую нельзя расширить для создания окончательной модели. В модели с правильным переплетением каждая вершина проходит ровно через одну грань ровно одного другого тетраэдра.
  Более точный критерий (который я считаю достаточно) выходит: любые два тетраэдра A и B из пяти расположены так, что:
  • Одна вершина A проходит через одну грань B и наоборот. Каждый тетраэдр имеет 4 вершины, и каждая вершина проходит ровно через одну грань ровно одного другой тетраэдр (каждый разный).
  • Грань грани A, противоположная вершине, проходящей через B, лежит в плоскости, параллельной плоскости грани B, противоположной вершине, проходящей через A.
  • Из 4-х граней тетраэдра А одна пересекается 3-мя гранями тетраэдра В (это грань, «проткнутая» В) и три других пересекаются ровно по одному ребру B каждый. Всего тетраэдров 5, и у каждого по 4 грани. Глядя на любой отдельный тетраэдр, можно сказать, что каждый его четыре грани протыкаются одной вершиной другого соседа. Проверка этого условия является хорошей проверкой, чтобы убедиться, что ваша модель в порядке в любой момент времени. например, все устройства, в которых какая-либо грань пересекается с двумя ребрами одного и того же тетраэдра, считаются неудачными.
• Рамы переплетаются довольно плотно. Даже когда установлены только три из пяти рам, у рам очень мало свободы движения. Если вы приедете при неполной модели более двух рамок и рамы распущены, свободно двигаются друг относительно друга, возможно, вы их неправильно сплели.
• Веселись! Сборка этой модели несколько ошеломляет и может разочаровать, если вы хотите закончить ее как можно быстрее. Это может занять много экспериментов, чтобы найти правильный способ плетения рамок, но это, безусловно, стоит потраченного времени.

Опубликовано: 3 декабря 2006 г. , Обновлено: 18 апреля 2021 г.

RCSB PDB — 4EGG: Computationally Designed Self-assembling tetrahedron protein, T310

• Structure Summary
• 3D View
• Annotations
• Experiment
• Sequence
• Genome
• Versions

PreviousNext

Macromolecule Content

• Общий вес структуры: 138,88 кДа и NBSP
• Количество атомов: 9,087 и NBSP
• Моделируемый счет остатков: 1,127 и NBSP
• . Способность. , T310
  
  

  ---

  Проверка wwPDB &nbsp &nbsp 3D-отчет&nbspПолный отчет

  
  

  Это версия записи 1.2. См. полную историю.

  King, N.P.,&nbspSheffler, W.,&nbspSawaya, M.R.,&nbspVollmar, B.S.,&nbspSumida, J.P.,&nbspAndre, I.,&nbspGonen, T.,&nbspYeates, T.O.,&nbspBaker, D.

  (2012) Science&nbsp 336 : 1171-1174

  • PubMed : & NBSP22654060 & NBSPSERCH ON PubMedSearch на PubMed Central
  • DOI: & NBSP 10.1126/Science.1219364
  
  
  • Pubmed Arhicelin . Белковые строительные блоки симметрично соединяются друг с другом, чтобы идентифицировать взаимодополняющие механизмы упаковки, а затем между строительными блоками разрабатываются низкоэнергетические межбелковые интерфейсы, чтобы стимулировать самосборку …

    Мы описываем общий вычислительный метод для проектирования белков, которые самособираются до желаемой симметричной архитектуры. Белковые строительные блоки симметрично состыкованы друг с другом, чтобы идентифицировать комплементарные механизмы упаковки, а затем между строительными блоками разрабатываются низкоэнергетические межбелковые интерфейсы, чтобы стимулировать самосборку. Мы использовали строительные блоки тримерных белков для разработки комплекса из 24 субъединиц диаметром 13 нм с октаэдрической симметрией и комплекса из 12 субъединиц диаметром 11 нм с тетраэдрической симметрией. Спроектированные белки собираются в желаемые олигомерные состояния в растворе, и кристаллические структуры комплексов показали, что полученные материалы точно соответствуют моделям дизайна. Этот метод может быть использован для разработки широкого спектра самособирающихся белковых наноматериалов.

    ---

    Организационная принадлежность :&nbsp

    Факультет биохимии, Вашингтонский университет, Сиэтл, Вашингтон, 98195, США.

    
    
  
  

  Макромолекулы

  Найдите похожие белки по: 

  (по порогу идентичности)  | 3D Structure

  Entity ID: 1
  Molecule	Chains	Sequence Length	Organism	Details	Изображение
  Предполагаемая ацетилтрансфераза SACOL2570	A, B, C, D, E, F A, B, C, D, E, F	1127 902 aureus COL	Mutation(s) : 10&nbsp Gene Names:&nbsp SACOL2570 EC:&nbsp 2. 3.1
  UniProt
  Find proteins for&nbspQ5HCZ5&nbsp (Staphylococcus aureus (штамм COL)) Explore&nbspQ5HCZ5&nbsp Перейти к UniProtKB: &nbspQ5HCZ5
  Группы объектов &nbsp
  Sequence Clusters	30% Identity50% Identity70% Identity90% Identity95% Identity100% Identity
  UniProt Group	Q5HCZ5
  Protein Feature View Expand
  Reference Sequence

  Small Molecules

  Ligands&nbsp1 Unique
  ID	Chains	Name / Formula / InChI Key	2D Diagram	3D Interactions
  GOL Запрос к GOL Загрузить CCD-файл идеальных координат	G [авторизация A], H [авторизация A], I [авторизация A], J [идентификация C], K [идентификация D], G [идентификация A], H [идентификация A], I [идентификация A], J [идентификация C], K [идентификация D] , L [Auth E], M [Auth E], N [Auth F]	Глицерол C 3 H 8 O 3 Pedcqbhivmgh-nah-n. 0345 1111121121121121121121121121121121121121121121121112111н 2 8 O 3 H	Взаимодействие с лигандом

  Экспериментальные данные и проверка

  Экспериментальные данные

  Unit Cell :

  Length ( Å )	Angle ( ˚ )
  a = 183.76	α = 90
  b = 90.84	β = 125.3
  c = 107.7	γ = 90

  Software Package:

  Software Name	Purpose
  DENZO	data reduction
  SCALEPACK	data scaling
  PHASER	phasing
  BUSTER-TNT	refinement
  PDB_EXTRACT	data extraction
  BUSTER	refinement

  
  

  Просмотреть более подробные экспериментальные данные0040 Автор(ы) показаний:&nbsp

  Савайя, М.