Ученые сложили белковые оригами-тетраэдры в клетках печени мыши
Биохимикам удалось сложить трехмерные структуры заданной формы из полипептидной цепи. Для этого ученые сконструировали белковые спирали, складывающиеся друг с другом определенным образом при взаимодействии аминокислотных остатков. Белки, состоящие из спиралей с заданными свойствами, способны формировать структуры в виде тетраэдров, пирамидок и призм как в растворе, так и в живых клетках. Новый тип самосборных белковых наночастиц, по аналогии с ДНК-оригами, может найти применение как в биомедицине, к примеру, для доставки лекарств, так и в других приложениях. Работа опубликована в Nature Biotechnology.
Способность биологических полимеров формировать вторичную и
третичную структуры привлекает биоинженеров, которые пытаются при помощи
рационального дизайна заставить ДНК и белки складываться нужным образом. Формирование
заданных структур нуклеиновыми кислотами благодаря свойству комплементарности известно
как ДНК-оригами и давно и успешно используется для разных задач.
ДНК состоит всего из четырех структурных блоков (A,T,G,C), которые взаимодействуют друг с другом строго ограниченным образом (A «спаривается» с T, а G с C). Белковые цепочки состоят из 20 аминокислот, которые могут взаимодействовать друг с другом в гораздо более широком спектре путем электростатических и гидрофобных взаимодействий. Благодаря этому природные белки формируют несколько десятков определенных третичных структур, и ученые показали, что это далеко не предел.
Исследователям из нескольких институтов Любляны в
сотрудничестве с коллегами из других европейских университетов удалось создать
алгоритм, позволяющий проектировать дизайн новых частиц с заданной трехмерной
структурой на основе существующих в природе спиральных белковых доменов. Чтобы продемонстрировать
работу алгоритма, авторы работы сделали белки в виде тетраэдра, четырехгранной
пирамиды и треугольной призмы.
В основу самосборных структур легли спиральные белковые домены типа coiled-coil (их можно назвать «суперспираль», хотя устоявшегося термина для них в русском языке нет). Такие домены часто используются в природе для взаимодействия белков друг с другом.
В эксперименте одна полипептидная цепь, то есть один белок, формировала одну геометрическую фигуру. Самая большая полипептидная цепь в эксперименте состояла более чем из 700 аминокислот. Ребрами фигуры служили те самые «суперспирали», которые образовывались при взаимодействии гидрофобных и заряженных аминокислотных остатков в составе отдельных спиралей. Отдельные домены были разделены гибкими линкерами, позволяющими формировать углы. Форму частиц, полученных
Чтобы продемонстрировать применимость полученных белковых
наночастиц в живых системах, авторы работы сначала экспрессировали белковые
тетраэдры в бактериях и показали, что в отличие от белков, полученных в
предшествующих работах, такие частицы хорошо складываются в клетках и при этом
растворимы, то есть в нужном виде содержатся в цитоплазме.
На следующем этапе тетраэдры экспрессировали в клетках человека. Для того чтобы подтвердить правильную сборку структуры внутри клетки, авторы «пришили» к разным концам белковой молекулы половинки репортерного белка. Если белковая цепочка складывалась в нужную структуру, из половинок собирался целый репортер, способный светиться. Оказалось, что фигуры собираются правильно и в клеточной линии, и в клетках печени мыши, куда исследователи доставили генетические конструкции, кодирующие тетраэдры. Дополнительно ученые подтвердили, что такие белковые частицы, хотя и не встречаются в природе, не активируют внутриклеточные защитные реакции и не вызывают иммунного ответа в организме.
Самосборные белковые частицы с заданной формой, по словам
исследователей, могут найти применение в разных областях молекулярной терапии.
Такие белки можно использовать не только как средство доставки (по аналогии с ДНК-структурами),
но и, к примеру, для создания генетически кодируемых вакцин, при помощи которых
в организме синтезируются наночастицы, содержащие на своей поверхности антигены.
Мы писали, что ранее ученым удалось создать гибридные наночастицы, состоящие из ДНК и белка.
Белковые «скрепки»
улучшили способность ДНК-структур к самосборке.
Дарья Спасская
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
Трафарет тетраэдра — 79 фото
Развертка правильного тетраэдра
Тетраэдр схема сборки для склеивания
Развертка правильного октаэдра
Тетраэдр правильные многогранники
Тетраэдр схема для склеивания
Чертеж тетраэдра для склеивания с размерами
Развертка правильного тетраэдра
Развертка правильного икосаэдра
Многогранники звездчатый октаэдр
Развертка правильной четырехугольной пирамиды
Неправильный тетраэдр развертка
Трехгранная пирамида чертеж
Мемный треугольник из бумаги
Развертка трехгранной пирамиды чертеж
Правильный тетраэдр развертка для склеивания
Усеченный тетраэдр развертка
Тетраэдр из бумаги схема
Правильный тетраэдр развертка для склеивания
Развертка правильного октаэдра
Треугольные фигуры
Развертка правильной четырехугольной пирамиды
Развертка правильной четырехугольной пирамиды
Объемный треугольник из бумаги
Развертка правильной четырехугольной пирамиды для склеивания
Звёздчатый октаэдр схема
Сакральная геометрия тетраэдр
Правильные многогранники развертки для склеивания гексаэдр
Схема развертки октаэдра
Развертка правильного икосаэдра
Стереометрия октаэдр
Треугольник тетраэдр
Треугольная пирамида тетраэдр
Платоновы тела правильные многогранники чертежи
Тетраэдр и пирамида
Правильный икосаэдр оригами
Тетраэдр это правильная пирамида
Додекаэдр развертка
Додекаэдр Сакральная геометрия
Развертка многогранника додекаэдр
Правильные многогранники додекаэдр
Треугольная и четырехугольная пирамида
Звездный тетраэдр развертка
Пирамида Геометрическая фигура
Тригональная пирамида и тетраэдр
Малый Кубо-Кубо-октаэдр развертка
Четырехугольная пирамида
Тритрагон триметраэдр
Четырехугольная пирамида
Развертка треугольника
Пирамидка для склеивания
Треугольная коробка развертка
Пирамида геометрия с треугольником в основании
Развертка правильного октаэдра
Звёздчатый октаэдр (звезда Кеплера)
Объемные геометрические фигуры из бумаги
Пирамида фигура развертка
Четырехугольная пирамида
Равносторонний треугольник пирамида
Меркаба звездчатый октаэдр
Тетраэдр рис
Фигура Меркабы Геометрическая Меркаба
Икосаэдр на а4
Вырежи и склей пирамиду
Правильная треугольная пирамида это тетраэдр
Пирамида геометрия четырехугольная
Четырехугольная пирамида
Произвольная четырехугольная пирамида
Пирамида Хеопса многогранник
Сакральная геометрия трилистник
Правильный икосаэдр развертка для склеивания
Октаэдр вписанный в тетраэдр
Развертка 4 угольной пирамиды
Танграм схемы из 7 деталей
Четырёхугольная пирамида из бумаги схема
Правильная пятиугольная пирамида
Правильная пятиугольная пирамида развертка
Третья звездчатая форма икосаэдра
Правильный тетраэдр DABC
Комментарии (0)
Написать
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Бирюзовая бумага для оригами — Etsy.de
Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
Найдите что-нибудь памятное, присоединяйтесь к сообществу, делающему добро.
( 265 релевантных результатов, с рекламой Продавцы, желающие расширить свой бизнес и привлечь больше заинтересованных покупателей, могут использовать рекламную платформу Etsy для продвижения своих товаров. Вы увидите результаты объявлений, основанные на таких факторах, как релевантность и сумма, которую продавцы платят за клик. Узнать больше. )
- Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Больше похоже на это
Диаграммы Вот список всех диаграмм на этом сайте.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Заметки о модульном оригами Диаграммы, доступные здесь, включают модули для построения усеченного куба, ромбикосододекаэдр, усеченный октаэдр, икосододекаэдр, курносый куб, курносый додекаэдр, усеченный икосаэдр, усеченный кубооктаэдр и т. д. (подобный скелету). Использование модулей, которые могут
углов, я смог разработать множество других геометрических моделей. ➤ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Авторские права как на диаграмму, так и на модель принадлежат Фрэнсису Оу. Пожалуйста, свяжитесь с ним, если вы хотите использовать их каким-либо образом.
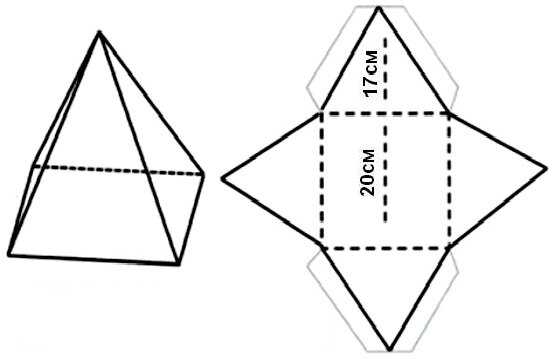сложенные, эти простые модули затем соединяются вместе без использования
клей для формирования полной модели. Я создал много модульных творений
используя разное количество простых модулей. Я также создал много многогранников.
Модели с использованием модулей. Складывание многогранных моделей является подмножеством модульных моделей.
Модели складные. Это модели, которые обычно восхищают математика.
Они также могут быть использованы в обучении и образовании.