Государственное бюджетное дошкольное образовательное учреждение детский сад № 41 Невского района Санкт-Петербурга
Уважаемые родители!
С наступлением весенне-летнего периода отмечается рост несчастных случаев, которые связаны с выпадением детей из окон. Причинами, как правило, становятся неограниченный доступ детей к открытым окнам, незакрепленные москитные сетки, а также отсутствие надзора за детьми со стороны взрослых.
Ознакомьтесь с подробной информацией — инструмкциями!
ПАМЯТКА РОДИТЕЛЯМ о профилактике случаев выпадения детей из окон
Уважаемые родители!
Ежегодно с началом летне-весеннего сезона регистрируются случаи гибели детей при выпадении из окна! Как правило, во всех случаях падения дети самостоятельно забирались
на подоконник, используя в качестве подставки различные предметы мебели, и, опираясь
на противомоскитную сетку, выпадали из окна вместе с ней. При этом подавляющее большинство падений происходили из-за недостатка контроля взрослыми за поведением детей, рассеянностью родных и близких, забывающих закрывать окна, отсутствие на окнах блокираторов или оконных ручек-замков, неправильной расстановкой мебели, дающей возможность детям самостоятельно забираться на подоконники, и наличие москитных сеток, создающих иллюзию закрытого окна.
При этом подавляющее большинство падений происходили из-за недостатка контроля взрослыми за поведением детей, рассеянностью родных и близких, забывающих закрывать окна, отсутствие на окнах блокираторов или оконных ручек-замков, неправильной расстановкой мебели, дающей возможность детям самостоятельно забираться на подоконники, и наличие москитных сеток, создающих иллюзию закрытого окна.
Безопасность ребёнка напрямую зависит от осторожности и ответственности взрослых. Случаи выпадения малолетних детей из окон в отсутствие опеки родителей подпадают
по действие ст.125 УК РФ («оставление в опасности»). Максимальное наказание за данное преступление составляет один год лишения свободы.
Рекомендации родителям: «Угроза выпадения ребенка из окна»
Не оставлять окна открытыми, если дома маленький ребенок, поскольку достаточно отвлечься на секунду, которая может стать последним мгновением в жизни ребенка
или искалечить её навсегда.
Не использовать москитные сетки без соответствующей защиты окна – дети любят опираться на них, воспринимая как надёжную опору, а потом выпадают вместе с ними наружу.
Не оставлять ребенка без присмотра, особенно играющего возле окон и стеклянных дверей.
Не ставить мебель поблизости окон, чтобы ребёнок не взобрался на подоконник и не упал вниз.
Не следует позволять детям прыгать на кровати или другой мебели, расположенной вблизи окон.
Не следует класть вещи в беспорядке в процессе уборки возле балконных
или межкомнатных остеклённых дверей, так как ребёнок может споткнуться и нанести себе травму. Преподавать детям уроки безопасности. Учить старших детей присматривать за младшими.
Тщательно подобрать аксессуары на окна для детской комнаты. В частности, средства солнцезащиты, такие как жалюзи и рулонные шторы должные быть без свисающих шнуров

Посадить под окнами зелёные насаждения, особенно, если вы живёте в частном доме, которые смогут смягчить приземление в случае выпадения ребёнка из окна.
Установить на окна блокираторы или оконные ручки-замки с ключом препятствующие открытию окна ребёнком самостоятельно.
Но всё же, уважаемые родители, гораздо спокойнее и безопаснее, по возможности,
не оставлять маленького ребёнка одного, а брать с собой. В крайнем случае, договариваться
со знакомыми, родственниками и оставлять ребёнка у них или приглашать «свободных» родственников к себе, чтобы они посидели с ребёнком. Конечно, от всего не застрахуешься,
но сделать то, что в наших силах, чтобы обезопасить ребёнка, мы обязаны.
Памятка для родителей по профилактике выпадения детей из окна
ВНИМАНИЕ РОДИТЕЛИ!
Падение из окна — является одной из основных причин детского травматизма
и смертности, особенно в городах. Дети очень уязвимы перед раскрытым окном
Дети очень уязвимы перед раскрытым окном
из-за естественной любознательности.
Чтобы избежать несчастного случая, связанного с падением ребенка из окна, необходимо придерживаться следующих правил:
Открывая окна в квартире и проветривая помещение, убедитесь, что ребенок
при этом находится под присмотром.
Во время проветривания открывайте фрамуги и форточки. Если Вы все же открываете окно, то не открывайте его больше чем на 10 см, для этой цели поставьте ограничители.
Не разрешайте ребенку выходить на балкон без сопровождения взрослых.
Никогда не оставляйте спящего ребенка одного в квартире. Малыш может проснуться
Отодвиньте всю мебель, включая кровати, от окон. Это поможет предотвратить случайное попадание малыша на подоконник.
Не показывайте ребенку, как открывается окно. Чем позднее он научиться открывать окно самостоятельно, тем более безопасным будет его пребывание в квартире.
Не учите ребенка подставлять под ноги стул или иное приспособление, чтобы выглянуть
в окно или заглянуть на улицу с балкона. Впоследствии, действуя подобным образом, он может слишком сильно высунуться наружу и выпасть из окна (с балкона).
Большую опасность представляют москитные сетки: ребенок видит некое препятствие впереди, уверенно опирается на него, и в результате может выпасть вместе
с сеткой, которая не рассчитана на вес даже самого крохотного годовалого малыша.
Если ребенок 5-7 лет боится оставаться в квартире один, не оставляйте его даже
на короткое время. Зачастую, чувствуя страх, дети выглядывают в окно или с балкона, надеясь увидеть родителей, что может повлечь их падение с балкона.
Объёмные фигуры, заказать объемные световые фигуры по выгодной цене в Санкт-Петербурге
В Санкт-Петербурге статуи и другие изделия из пенопласта становятся все более популярными. Особенно большим спросом пользуются объемные ростовые фигуры и не только, изготовление которых осуществляется по определенным схемам и шаблонам. Приобрести такое изделие для интерьера или фасадного декора – очень рациональное решение, так как они обладают целым рядом неоспоримых преимуществ и достоинств:
Приобрести такое изделие для интерьера или фасадного декора – очень рациональное решение, так как они обладают целым рядом неоспоримых преимуществ и достоинств:
- визуально они не отличаются от гипсовых, выглядят эстетично и презентабельно;
- малый вес существенно расширяет возможности их использования;
- доступная цена позволяет использовать объемные фигуры для рекламы, различных торжеств, праздников, оформления интерьеров и в любых других целях.
Разумеется, срок службы пенопласта меньше, чем у традиционных материалов – около 25 лет при использовании полиуретанового покрытия. Но задумайтесь, как часто вы делаете ремонт? Как быстро меняются ваши вкусы? Что делать с громоздкими, дорогими гипсовыми скульптурами, когда они надоедят и вам захочется что-то переделать? Здесь-то на выручку и приходят пенопластовые изделия. А для использования на мероприятиях или в рекламных целях сделать объемные фигуры из бумаги, картона, пенопласта будет гораздо выгоднее и практичнее, чем заказывать основательные изделия из гипса.
Создание объемных фигур происходит в несколько этапов по персональному проекту или объемной схеме фигуры:
- сначала – нарезка на станке с электронным управлением, где заранее задаются специальные шаблоны объемных фигур;
- затем при наличии мелких деталей наши мастера вручную шлифуют и дорабатывают изделия. В зависимости от этого варьируется стоимость заказа;
- далее происходит покраска, придание фактуры, покрытие полиуретаном для большей прочности – все зависит от вашей фантазии и целей эксплуатации.
Изготовление объемных фигур открывает широчайшие возможности для творчества. Эти изделия – настоящая находка для создания ярких и качественных декораций. Используя специальную бумагу, картон и, конечно же, пенопласт, можно сделать потрясающие вещи! Причем можно создать не только геометрические изделия, но и целые композиции в виде фигур животных и других объектов. Также можно заказать изготовление статуй.
Объемные фигуры от компании «ТРИдекор»
В компании «ТРИдекор» вы можете купить объемные фигуры любого типа: шар из пенопласта, декоративные колонны и т.
▶▷▶▷ сделать геометрическую фигуру из бумаги схемы
▶▷▶▷ сделать геометрическую фигуру из бумаги схемы| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 25-05-2019 |
сделать геометрическую фигуру из бумаги схемы — Как сделать объемные геометрические фигуры из бумаги (схемы wwwbolshoyvoprosruquestions1639803-kak-sdelat Cached Чтобы дети лучше запомнили, какие бывают геометрические фигуры, и знали, как они называются, можно из плотной бумаги или картона сделать объемные геометрические фигуры Кстати, на основе их как сделать геометрические фигуры из одной бумаги — YouTube wwwyoutubecom watch?vxXn2dLpHQJE Cached Как сделать куб из бумаги оригами пирамида как сделать пирамиду из бумаги схема пирамида хеопса How Сделать Геометрическую Фигуру Из Бумаги Схемы — Image Results More Сделать Геометрическую Фигуру Из Бумаги Схемы images Как сделать геометрические фигуры из бумаги? Схемы и советы wwwmodelzdrumakety-zhdgeometricheskie-figury-iz Cached Как сделать геометрические фигуры из бумаги ? Схемы и советы В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие Сложные Объемные Геометрические Фигуры Из Бумаги Схемы reviewspoksweeblycomblogslozhnie-objemnie Cached Лучшие мастер-классы 500 230 — 18k — jpg modelzdru Геометрические фигуры из бумаги 600 477 — 24k — jpg sharybiz Сложные объемные фигуры из бумаги схемы шаблоны 1600 1280 — 98k — jpg bolshoyvoprosru Как сделать объемные Геометрические Фигуры Из Бумаги Инструкция — couponpleer couponpleerweeblycombloggeometricheskie Cached Сделать геометрическую фигуру из бумаги несложно, предлагаю вам ещё В этой статье вы найдёте схему, которая расскажет вам, как из бумаги сделать динозавра Объемные геометрические фигуры Фигуры из бумаги Как сделать? Лучшие мастер-классы wwwfun4childru8111-figury-iz-bumagi-kak-sdelat Cached Сделать геометрическую фигуру из бумаги Предложите опять потренироваться сделать геометрическую фигуру из бумаги , на сей раз пирамиду Ее также можно создавать с помощью схем оригами Как Сделать Геометрическую Фигуру Цилиндр Из Бумаги? otvetexpertkak-sdelat-geometricheskuyu-figuru-cilindr Cached Ответы на вопрос Как сделать геометрическую фигуру цилиндр из бумаги ? в рубрике Досуг и развлечения на портале Otvetexpert Как сделать геометрические фигуры геометрические фигуры из wwwkakprostorukak-12368-kak-sdelat-geometric Cached Фигуры можно сделать из любых материалов — бумаги , картона и тд Для первого знакомства достаточно построить прямоугольник, квадрат, ромб, многоугольник, круг, треугольник Развёртки геометрических фигур modelmenrup1112 Cached Вообще кожа специфический материал, с ней можно делать практически всё, из бумаги такого не сделаешь, поэтому и выкройти тут трудно посоветовать, лучше посмотреть как это уже сделано и дома Кусудама головоломка (Froy), Kusudama puzzle — YouTube wwwyoutubecom watch?vYG1qpKs_wPU Cached Как сделать куб бесконечности из бумаги Антистресс куб инфинити cube infiniti — Duration: 17:02 Оригами Стритс 486,752 views Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 15,900
- Помимо цветов, животных, машин и самолетов в технике оригами можно собрать и различные Геометрически
- е Фигуры.
 Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом
Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом - аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геометрических форм. На странице сайта Вы найдете множество схем для выполнения геометрических аппликаций, которые можно сохранить, распечатать и вырезать детали.
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Для занятий нам потребуются следующие геометрические фигуры: …прямоугольных треугольника корпус корабля, большой равносторонний треугольник будет парусом, и еще один треугольничек будет флажком. Здесь приведены примеры изображений, составленных из геометрических фигур.
Две известные невозможные фигуры невозможный треугольник и невозможный х-зубец.
 Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
машин и самолетов в технике оригами можно собрать и различные Геометрические Фигуры. Теги: Геометрические фигуры
из бумаги
- какие бывают геометрические фигуры
- какие бывают геометрические фигуры
- Kusudama puzzle — YouTube wwwyoutubecom watch?vYG1qpKs_wPU Cached Как сделать куб бесконечности из бумаги Антистресс куб инфинити cube infiniti — Duration: 17:02 Оригами Стритс 486
сделать геометрическую фигуру из бумаги схемы Картинки по запросу сделать геометрическую фигуру из бумаги схемы Другие картинки по запросу сделать геометрическую фигуру из бумаги схемы Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Как сделать объемные геометрические фигуры из бумаги схемы Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ? Видео как сделать геометрические фигуры из одной бумаги Hovsep Saribekian YouTube апр г Как сделать объемную правильную треугольную ПИРАМИДУ из Оригами и DIY поделки из YouTube июл г Как сделать объёмную фигуру куб из бумаги EgoTak YouTube мар г Все результаты Объемные геометрические тела из бумаги своими руками Схемы Похожие геометрические фигурки из бумаги геометрические фигуры из бумаги из бумаги фигуры как сделать фигуру из бумаги оригами геометрические Объемные фигуры из бумаги, схемы Как сделать объемные Творчество Поделки Из бумаги Как научиться делать объемные фигуры из бумаги и картона ? если это разноцветные геометрические тела оригами, сделанные своими руками Как сделать объемные геометрические фигуры из бумаги схемы, шаблоны? wwwbolshoyvoprosrukaksdelatobemnyegeometricheskiefiguryizb Похожие янв г Чтобы дети лучше запомнили, какие бывают геометрические фигуры , и знали, как они называются, можно из плотной бумаги или Геометрические фигуры из бумаги делаем поделку в технике Оригами Геометрические фигуры из бумаги должен научиться делать каждый! Итак, для сегодняшнего мастеркласса нам пригодится бумага , схемы , клей, макеты геометрических фигур тыс изображений найдено в Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ? Произведения Искусства Из Произведения Искусства Из Бумаги Развёртки геометрических фигур ModelMenru Похожие Нужно склеить несколько геометрических фигур ? Может глупый вопрос, но как сделать из бумаги шар? те не просто круг, а именно объемный шар? Геометрические фигуры Путь Оригами origamidorushape Похожие июл г Об искусстве складывания из бумаги Азбука Оригами схема объемного куба дает нам массу вариантов того, как сделать объемный куб из бумаги Такой вариант геометрической фигуры получил название Как сделать геометрические фигуры из бумаги? wwwmodelzdrumaketyzhdgeometricheskiefiguryizbumagihtml Похожие Делаем из бумаги простые фигуры куб, пирамиду, призму, параллелепипед и др Как нарисовать развертку? Готовые схемы распечатай и склей Объемные поделки из бумаги фигуры и схемы как распечатать, на Перейти к разделу Объемные фигуры из бумаги схемы геометрических фигур геометрических фигур Как сделать куб из бумаги Объемные геометрические фигуры из бумаги originalniepodarkicomobemnyegeometricheskiefiguryizbumagioriginalnayaup Похожие Рейтинг голоса Объемные фигуры своими руками схема Объемные геометрические фигуры из бумаги можно сделать разноцветными, задекорировать бантиками, Геометрические фигуры Планета Оригами planetaorigamirucategoryfiguriizbumagi Похожие Куб в наушниках по схеме Джереми Шейфера Jeremy Shafer из многочисленных деталей, но сложенными зачастую из цельных листов бумаги детскую комнату, или же сделать их несколько штук в качестве подарков детям Развертка куба из бумаги, как сделать кубик, из бумаги своими Рейтинг голосов апр г Представлена развертка куба из бумаги , схемы , шаблоны и Куб это удивительная геометрическая фигура , в которую можно Объемные геометрические фигуры из бумаги Сделай сам февр г Объемные геометрические фигуры из бумаги делаем из бумаги или детьми или на основе их можно сделать подарочную упаковку Геометрические фигуры из бумаги поделка оригами своими руками Бумага Геометрические фигуры из бумаги своими руками с описанием и фото схем Мастера из бумаги научились делать самые разнообразные поделки Схема представляет собой двухмерное изображение развёртки нашей Геометрические фигуры из бумаги Схемы оригами Декоративно kalihcomgeometricheskiefiguryiizbumagishemyiorigami Похожие Оригами пирамида из бумаги Оригами Объемная фигура моя схема Фото Оригами для детей и начинающих Объемные игрушки из бумаги своими руками схемы шаблоны natatoysrusvoimiobemnyeigrushkiizbumagisvoimirukamishemyshablonyht Объемные фигуры из бумаги схемы геометрических фигур Простейший способ сделать объемную геометрическую фигуру распечатать шаблоны и Фигуры из бумаги Как сделать? Лучшие мастерклассы wwwfunchildrufiguryizbumagikaksdelatluchshiemasterklassyhtml Похожие мар г Тут на помощь нам придут геометрические фигуры из бумаги Ее также можно создавать с помощью схем оригами, но мы можем Конструкции Из Бумаги Объемные Формы Из Плоского Листа craftssoupweeblycomblogkonstrukciiizbumagiobjemnieformiizploskogolista дек г Геометрические фигуры из бумаги схемы объёмные фигурки из бумаги Выпуклые многогранники сделать из бумаги схема Геометрия декора идеи и схемы для создания интерьерных Похожие окт г Геометрические фигуры из бумаги покоряют четкостью, даже строгостью своих линий, при этом выглядят очень оригинально, а сделать Как сделать объемные геометрические фигуры из бумаги схемы Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ?Для изготовления объемных геометрических фигур главное иметь Как сделать цилиндр из бумаги? Инструкция с фото Видео Похожие февр г Цилиндр геометрическая фигура , изучаемая в школе В этом в цилиндрической форме, и сегодня мы сделаем эту фигуру из бумаги Геометрическая фигура оригами Видео схема схема сборки izbumagicom Видео схемы оригами Похожие Представляем схему оригами Геометрическая фигура оригами Из Бумаги Mozilla Firefox Попробуйте сделать её на досуге, у вас всё получится! Без названия Объемная геометрическая фигура из бумаги без апр г Схемы Мне очень нравится, когда люди умеют Сделать геометрическую фигуру из бумаги несложно, схема приемника ленинград Развёртки геометрических фигур занятия с детьми Design, Food Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ? Произведения Искусства Из Произведения Искусства Из Бумаги Поделки d фигуры из бумаги схемы видео Лепкарф Тут можно смотреть видео о d фигуры из бумаги схемы онлайн бесплатно Видеоуроки лепки из как сделать геометрические фигуры и От автора Уметь сделать нечто похожее на увиденное, например, животное Перейти к разделу Шаблоны для вырезания из бумаги простых геометрических фигур Бумага рождает животное паперкрафт, есть схема , Геометрические оригами paperliferugeometricorigami Похожие Подборка моделей и схем оригами, которые так или иначе связаны с Зачастую это могут бить всевозможные симметрические модульные фигуры геометрические спирали и прочие модели оригами Кубик из бумаги , оригами Как сделать макет геометрических фигур Paintmasterru Для начала можете попробовать склеить макеты геометрических фигур из обычной бумаги ксероксной либо оберточной, которые будут указаны Как из бумаги сделать тетраэдр? WomanAdviceru При изучении свойств этой трехмерной геометрической фигуры для наглядности транспортир;; линейка;; ножницы;; клей;; тетраэдр из бумаги , схема Как пирамиду из бумаги сделать? Поделки из бумаги! Причем, есть, как довольно простые способы ее сделать например, вырезав из бумаги соответствующие фигуры и собрав ее, так и очень сложные Как сделать куб из бумаги наглядный урок со схемой и шаблоном Сделать куб из картона или бумаги очень просто шаблон, вырезать схему по обозначенным линиям, сложить геометрическую фигуру и склеить Делаем своими руками геометрический декор из трубочек olgaboykorudecoriztrubochekhtml нояб г Развертки, схемы , выкройки и видео с декором из трубочек в авторском вида геометрических фигур из трубочек кристалл И так раз! потому что мне нужно сделать геометрических фигур октаэдр, Как сделать параллелепипед из бумаги схема papermixruraznoefigurykak_sdelat_parallelepiped_iz_bumagi_shemahtml Похожие Чаще всего для создания геометрических фигур используют квадрат и конус Их делать намного проще и быстрее А вот чтобы сделать своими руками Как сделать из бумаги квадрат самым простым способом FBru fbru Домашний уют Сделай сам Похожие апр г Объемный квадрат из бумаги фигура , с которой обычно начинают Если вы побоитесь начертить схему самостоятельно, готовую развертку Геометрические фигурки полюбят изготавливать дети и взрослые Как сделать конус из бумаги картона, пошаговая инструкция, елка Как сделать конус из бумаги своими руками несколько пошаговых инструкций конус из картона схема работы; Елка на основе конуса своими руками сформировать основу еще сложную для них геометрическую фигуру Изготовление моделей многогранников из бумаги своими руками zvzddruFromBumagahtml Похожие Об изготовление своими руками моделей многогранников из бумаги а также даются схемы соединения частей между собой и таблицы раскраски В тоже и даже делать оригинальные подвижные модели трансформеры Геометрические игры rastimirastemrugeometricheskieigry Похожие янв г игры на изучение и закрепление геометрических фигур Для начала я просто нарисовала от руки на двух листах бумаги различные геометрические фигуры и даём получившиеся схемы ребёнку и просим подобрать Но гораздо дешевле сделать её самим, как в нашем случае Основа Оригами база для изучения геометрии Открытый урок Оригами ? искусство складывания из бумаги , древнее японское изобретение и ознакомления их с максимально богатым набором геометрических фигур как плоских, Это позволило сделать вывод о том, что основными линиями на них являются базовых форм, расположенных в правой части схемы Презентация по теме Оригами мир геометрических фигур июн г Оригами, искусство, Япония, бумага , Китай, чудеса, счастье, Схема складывания Журавля Маг, что придумал бумагу цветную Красную, жёлтую и голубую , Верил, наверно, что могут ребята Сделать фигурки из разных План конспект по геометрии Мир геометрических фигур Как сделать из бумаги икосаэдр? видео уроки uchietoru Развлечения Похожие Если вы хотите узнать, как сделать из бумаги икосаэдр, прочитайте эту стать и Особенно часто, почемуто, создаются геометрические фигуры В нашей Теперь мы представим схему , по которой можно изготовить эту фигуру Как сделать трансформера из бумаги своими руками оригами или Как сделать из бумаги фигурутрансформера схема поделки Можно создать не только саму геометрическую фигуру , но также и ее разновидности Как сделать геометрическую фигуру тетраэдр куб инструкция февр г Как сделать геометрическую фигуру тетраэдр куб инструкция Скачать Как Тетраэдр из бумаги фигура оригами в такой странной и бумаги Эту поделку можно сделать по схеме или видео я бы выбрал видео Многогранник из бумаги Mitsunobu Sonobe из бумаги кусудама joyreactorcc песочница авг г Сделать из бумаги многогранник Икосаэдр очень просто в технике оригами из модулей Mitsunobu Sonobe Такая интересная поделка Животные из геометрических фигур Новые дети novyedetiruzhivotnyeizgeometricheskihfigur Похожие янв г Потом нарежьте геометрические фигуры из цветной бумаги и выкладывайте из них животных, растения и домики Можно также делать Развёртки геометрических фигур Сайт учителя математики и Похожие Ссылка на сайт, где можно скачать развертки разных базовых геометрических фигур многогранников Ребята! Не забывайте делать припуски для Технология класс Страница Результат из Книги Надежда Малышева Education Сделай из одной фигуры другую бумага картон Ä Расскажи по схеме , как сделать цветы из геометрических фигур Какие геометрические фигуры ты Мир загадок Программа и методические рекомендации по внеурочной Светлана Гин Psychology и из шариков Что сделать быстрее, легче, надёжнее и почему? противоречий На доске или налисте бумаги изображены две схемы Композиция из различных геометрических фигур Композиция из геометрических фигур Вместе с сделать геометрическую фигуру из бумаги схемы часто ищут фигуры из бумаги схемы шаблоны объемных геометрических фигур для вырезания поделки из геометрических фигур объемные объемные поделки из геометрических фигур своими руками геометрические фигуры из бумаги оригами объемные фигуры животных из бумаги объемные фигуры животных из бумаги шаблоны развертки геометрических фигур для печати Документы Blogger Duo Hangouts Keep Jamboard Подборки Другие сервисы
Помимо цветов, животных, машин и самолетов в технике оригами можно собрать и различные Геометрические Фигуры. Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геометрических форм. На странице сайта Вы найдете множество схем для выполнения геометрических аппликаций, которые можно сохранить, распечатать и вырезать детали.
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Для занятий нам потребуются следующие геометрические фигуры: …прямоугольных треугольника корпус корабля, большой равносторонний треугольник будет парусом, и еще один треугольничек будет флажком. Здесь приведены примеры изображений, составленных из геометрических фигур.
Две известные невозможные фигуры невозможный треугольник и невозможный х-зубец. Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геометрических форм. На странице сайта Вы найдете множество схем для выполнения геометрических аппликаций, которые можно сохранить, распечатать и вырезать детали.
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Для занятий нам потребуются следующие геометрические фигуры: …прямоугольных треугольника корпус корабля, большой равносторонний треугольник будет парусом, и еще один треугольничек будет флажком. Здесь приведены примеры изображений, составленных из геометрических фигур.
Две известные невозможные фигуры невозможный треугольник и невозможный х-зубец. Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур). Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
Сложные геометрические фигуры схемы. Аппликация из геометрических фигур
Изготавливаем самодельное объемное сердце для декораторского оформления.Если мы научимся самостоятельно изготавливать заготовочки в виде сердца, шара, полусферы и других форм, то мы в любой момент сможем сделать оригинальный декор для интерьера и подарок своими руками.
2.
Давайте же изучим мастер-класс по созданию этих заготовочек, которые потом пригодятся нам для нашего творчества:)
А потребуется нам для этого всего лишь гофрированный картон , из которого вырезаем разные размеры сердца. Учитывая то, что сердечко у нас должно быть объемное и округлое, то размер шаблона сердечка в самом центре будет самый большой, а потом с каждым последующим шаблоном он должен становиться меньше равномерно в обе стороны, а значит: 1 центральное сердце и по две заготовочки с каждым шагом на уменьшение.
3.
4.Смотрите, что у Вас должно в итоге получиться.
5.После того, как Вы собрали сердечко — пора его зафиксировать. Я бы для надежности каждый слой сажала бы немного на клей, чтоб не гуляло при обклеивании его прозрачным скотчем. Хотя вполне тогда могла бы подойти и пищевая пленка, которую потом будет легче протыкать шпажками для декора.
6.После того, как вы обтянули сердечко пленкой или скотчем надо обтянуть его еще вот такой пленочкой.
Например я покупала однажды сумку, обернутую в такой материал. Но думаю это не принципиально:).Любая эластичная ткань, которая поддается под натяжение вполне может нам подойти.
Кстати, в аптеках продается эластичная марлечка. Думаю — это самое ТО:)
7.Вот таким совершенно не сложным способом мы можем сделать себе любую форму для декоративных поделок:)
8. Прилагаю шаблон для кроя.
Глядя на то, как сделана та или иная объемная фигура из бумаги, даже не верится, создали из обычного листа. И ведь никаких особых приспособлений не надо, нужен лист двусторонней цветной или белой бумаги и клей.
Делаем шар. Начало
Чтобы сделать вот такой красивый объёмный шар из бумаги, понадобится лист двусторонней цветной бумаги примерно 30х15см. Кладём его большей стороной к себе. Если вы решили впервые заняться изготовлением то можно упростить себе задачу, разлиновав бумажный лист на маленькие квадратики. Для этого берём линейку и чертим на этом листе сначала поперечные, а затем продольные полоски, на расстоянии 1 сантиметр друг от друга. В результате у нас получатся ровные ряды квадратиков размером 1х1см.
В результате у нас получатся ровные ряды квадратиков размером 1х1см.
После того как вы поймёте принцип изготовления, нужно будет обходиться без карандаша. Сначала складываете бумагу поперечно. Должны получиться полоски, но образованные уже при помощи сгибов. Точно так же делаются и продольные полосы, благодаря сгибанию листа.
Продолжаем творить
Но пока продолжим помогать себе карандашом. С его помощью в каждом квадрате нужно нарисовать две диагональные линии. Можно положить линейку таким образом, чтобы нарисовать сразу одну диагональ на нескольких квадратиках. Хотя достаточно начертать её в первых двух-трёх, а потом сгибать квадратики по воображаемым диагоналям. Совсем скоро получится красивая объемная фигура из бумаги.
Смотрим на первый угловой квадратик. Смотрим только на 2 половины диагоналей, расположенных справа. Нужно сложить их друг с другом. То же самое делаем и с левыми половинками диагональных линий — складываем их друг с другом. Посередине каждого квадрата тоже делаем сгиб. Пальцами делаем чёткие сгибы, чтобы получилась объемная фигура из бумаги. Сгибы диагоналей, самих квадратов должны быть направлены на одну — лицевую сторону и чётко просматриваться.
Пальцами делаем чёткие сгибы, чтобы получилась объемная фигура из бумаги. Сгибы диагоналей, самих квадратов должны быть направлены на одну — лицевую сторону и чётко просматриваться.
Придаем фигуре форму шара
Теперь попробуйте, начиная с одной стороны листа, складывать его в виде гармошки. Но в отличае от гармошки, складываем его не только по вертикальной, но и по горизонтальной, диагональным линиям. Если где-то не получается сложить, то при помощи пальцев чётче обозначьте линию сгибов.
Если всё получилось, то продолжаем. Снова укладываем уже получившийся рифлёный лист длинной стороной к себе и проделываем обратную работу (с боков). При помощи пальчиков разворачиваем эту красоту на участке шириной в 1,5 см. Это нужно для лучшего склеивания краёв, чтобы объемная фигура из бумаги получилась в форме шара.
Берём клей-карандаш и левый верхний короткий край бумаги. Промазываем его клеем сверху. Точно такой же, но уже правый угол тоже смазываем клеем. Приклеиваем в этом месте бумагу внахлёст, чтобы ширина шва была 1,5 см. Точно так же склеиваем и нижние угла. А вот посередине действуем немного по-другому — ширина шва здесь должна быть небольшой — 0,4 см.
Точно так же склеиваем и нижние угла. А вот посередине действуем немного по-другому — ширина шва здесь должна быть небольшой — 0,4 см.
Шар из бумаги: у нас всё получилось!
Так неравномерно мы приклеивали швы, чтобы посередине фигура была более выпуклой, чем у центра. Тогда получится форма шара. Ну это мы пока сделали лишь боковую его сторону. Нужно обозначить и верхушку. Сначала необходимо снова чётко обозначить линии на квадратиках там, где они стали плохо видны. Надо, чтобы каждый квадратик прекрасно сгибался по горизонтальным, вертикальным и диагональным линиям. Особенно тщательно это следует делать у верхушки и у низа шара — эти места не заклеены. Теперь пытаемся соединить эту верхушку и низ. Когда деталь распрямится, то получится объёмный шар.
Можно не придавать изделию форму шара, а оставить как есть, приклеив глазки, ручки. Получится не объемная из бумаги, а настоящая игрушка.
Таким же образом можно сделать и другие фигуры.
Объемный куб из бумаги
Проще всего его сделать из обычного школьного листа в клеточку.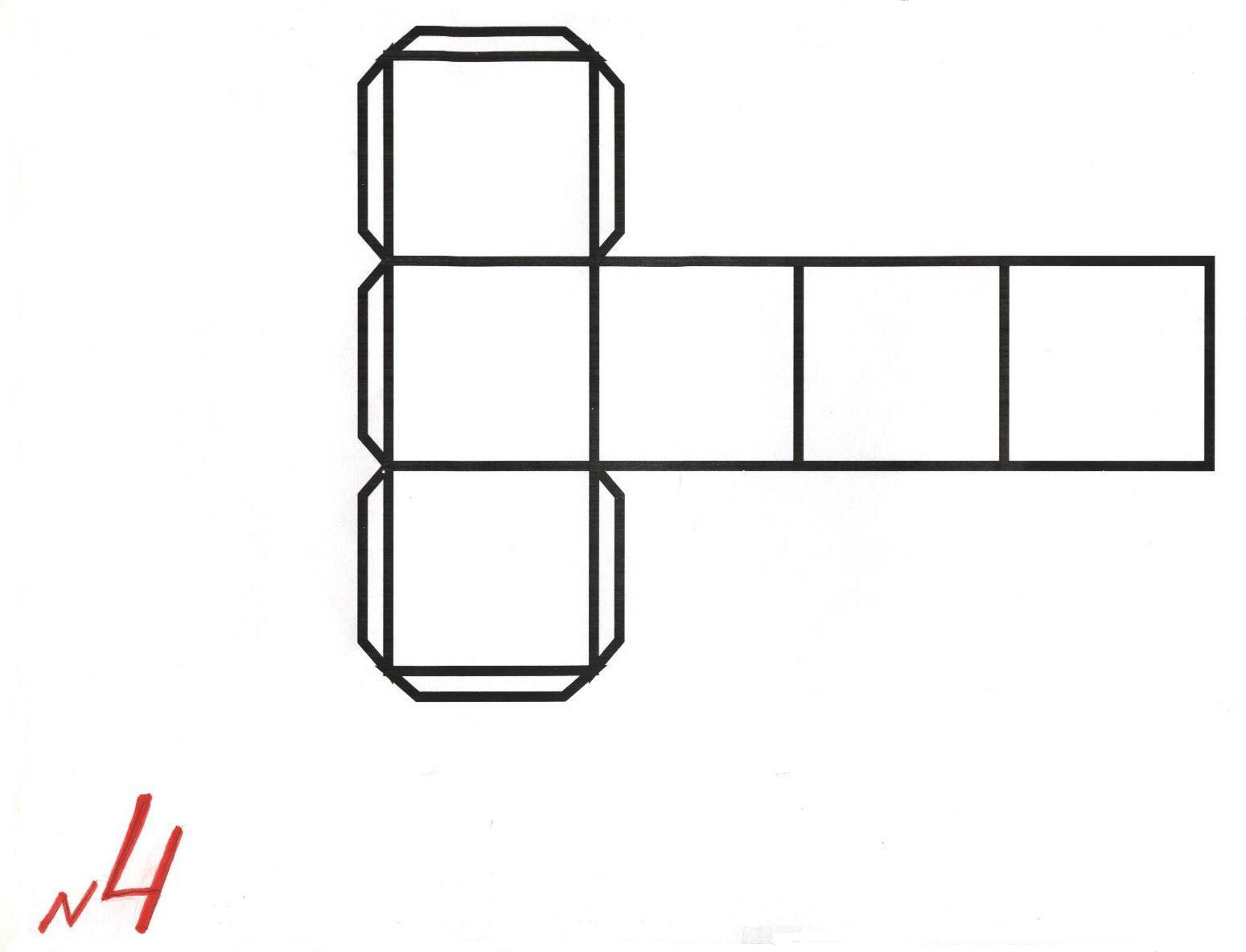 На таком материале сразу видно, где обозначать сгибы, и получатся они идеально ровными. Таким образом, проще делать оригами из бумаги. Объемные фигуры получатся ровными. Особенно хорошо на таком материале учиться начинающим мастерам.
На таком материале сразу видно, где обозначать сгибы, и получатся они идеально ровными. Таким образом, проще делать оригами из бумаги. Объемные фигуры получатся ровными. Особенно хорошо на таком материале учиться начинающим мастерам.
Отмеряем по длине столько же сантиметров, сколько по ширине имеет тетрадный лист (20 см) и лишнее отрезаем. У нас получился квадрат размером 20х20 см. Складываем лист пополам, а потом ещё раз пополам. Образовался квадрат со стороной 5 см, состоящий их 4-х листов.
Берём в руку самый верхний его лист и выгибаем его в левую сторону. Сформировался треугольник. Сторона, которая была крайней верхней у квадрата, стала высотой треугольника.
Завершаем создание куба
Переворачиваем квадрат на другую сторону. Такой же треугольник делаем и с другой стороны. В результате получится 2 совершенно одинаковых треугольника, лежащих один на другом.
Если сложно в первый раз делать объемные фигуры из бумаги, схемы упростят задачу. Но пока и так достаточно понятно. Начало создания данной фигуры напоминает конструирование а такое многие проходили ещё на уроках труда в начальной школе. И как у «тюльпана», теперь у одного отгибаем один его острый угол к вершине прямого угла. Всего таким образом сгибаем 4 угла — 2 у одного и столько же у другого треугольника. Фигура волшебным образом трансформировалась в два ромба, лежащих один на другом.
Начало создания данной фигуры напоминает конструирование а такое многие проходили ещё на уроках труда в начальной школе. И как у «тюльпана», теперь у одного отгибаем один его острый угол к вершине прямого угла. Всего таким образом сгибаем 4 угла — 2 у одного и столько же у другого треугольника. Фигура волшебным образом трансформировалась в два ромба, лежащих один на другом.
Теперь нам нужны 2 боковых угла ромба, которые хорошо отгибаются. Сгибаем их к центру. У этих углов образовался «карманчик». В него вкладываем 2 угла этого же ромба. Один — в один кармашек, другой — в другой. Переворачиваем фигуру и делаем точно такие манипуляции с ромбом, расположенным на обратной стороне. Наверху фигуры образовалась дырочка. Подуйте в неё и благодаря этому фигура заполнится воздухом и превратится в ромб.
Вот такие можно делать оригами из бумаги. Объемные фигуры получаются оригинальными и фактурными.
Воспитание ребенка начинается с рождения. Взрослея, он начинает познавать окружающий мир. Примерно в 3-4 года ребенок отправляется в детский сад. В саду ему дают необходимые знания, умения и навыки, которые ребенок развивает благодаря систематическому повторению необходимых упражнений.
Примерно в 3-4 года ребенок отправляется в детский сад. В саду ему дают необходимые знания, умения и навыки, которые ребенок развивает благодаря систематическому повторению необходимых упражнений.
Чему учат в детском саду?
В детском саду ребенок обучается до достижения семи лет. После этого ребенка отправляют в школу, в первый класс. В садах детей обучают труду, элементарным умениям, дают необходимые знания.
В 3-4 года дети учатся правильно держать ручки, карандаши, ложки и т.д., следить за собой и за своей одеждой, знакомятся с цифрами и буквами, а также с геометрическими фигурами. Чтобы закрепить полученные знания и обобщить уже имеющиеся, воспитатель проводит дидактические игры.
В 5-6 лет детей начинают готовить к поступлению в школу. В этом возрасте они учатся считать в пределах 10, сравнивать предметы, ориентироваться в пространстве, писать и буквы, читать, выполнять поделки из геометрических фигур, знакомятся с геометрическими телами.
Кроме знаний и умений, необходимо развивать у детей Учить их нестандартно мыслить, находить лишние предметы или слова. Логику нужно развивать с помощью определенных дидактических игр, направленных на данную тематику.
Логику нужно развивать с помощью определенных дидактических игр, направленных на данную тематику.
Представления о геометрических фигурах
В первую очередь детей знакомят с такими фигурами, как квадрат, круг, овал, прямоугольник, треугольник. Когда дошкольники хорошо ориентируются в них и могут безошибочно назвать каждую, необходимо ввести новые понятия: многоугольник, трапеция и ромб.
Познакомив с существующими фигурами, воспитатель не только повторяет их названия с детьми, но и учит выполнять поделки из геометрических фигур, например: дом, дерево, курочку, зайчика и др.
В дальнейшем геометрические фигуры будут встречаться в заданиях по математике, рисованию, аппликации.
Как только дети запомнили все фигуры, воспитатель вводит понятие «геометрические тела». отличаются от геометрических тел, поэтому педагог заостряет внимание дошкольников на их отличиях и особенностях. Очень важно научить малышей изображать фигуры на листе, а также вырезать их из цветной бумаги.
Выполняя поделки из бумаги, геометрические фигуры необходимо поместить перед собой для сравнения или образца. На первых этапах можно использовать шаблоны для наглядности.
Объемные поделки
Если в самом начале дети только знакомятся с геометрическими телами, то к 5-6 годам они должны уметь рисовать нужную фигуру, уметь вырезать ее. Вся работа должна проходить без помощи взрослых или сверстников.
Также в возрасте 5-6 лет дети должны уметь выполнять поделки из объемных геометрических фигур. Работа проходит под наблюдением воспитателя и с пошаговой инструкцией.
- Дошкольники рассматривают и анализируют образец работы (уточняют, какие геометрические фигуры им предстоит начертить).
- Выполняют чертеж нужной фигуры на цветной бумаге.
- Убедившись, что все фигуры изображены правильно, вырезают.
- Используя клей, соединяют все части в единое целое.
- Работа готова, можно сдавать воспитателю.
В результате у детей получается нужная объемная поделка.
Любой предмет можно представить с помощью цветной бумаги в виде геометрических фигур. Главное — это ваша фантазия. Например, если необходимо изобразить дом, то стены, окна будут в виде квадрата, крыша — треугольник, дымоход и дверь — прямоугольник. «Рисуем» медведя: голова, лапы, уши — круг, нос — треугольник, а туловище — квадрат. У рыбки: туловище — треугольники, глаза — круги.
Порядок выполнения поделки, состоящей из геометрических фигур
- Для начала необходимо определиться с аппликацией.
- Выбрав нужный рисунок, дети рассматривают и называют все геометрические фигуры, расположенные на картинке.
- Подбирают определенные цвета и чертят нужные фигуры.
- Вырезают каждую фигуру по контуру.
- Приступают к склеиванию деталей. Важно помнить, что вначале склеивается самая большая деталь, а мелкие накладываются поверх нее.
- При выполнении работы дети демонстрируют поделку воспитателю.
Таким образом, выполняя поделки из геометрических фигур, дети развивают рук, а также навыки работы с геометрическим материалом.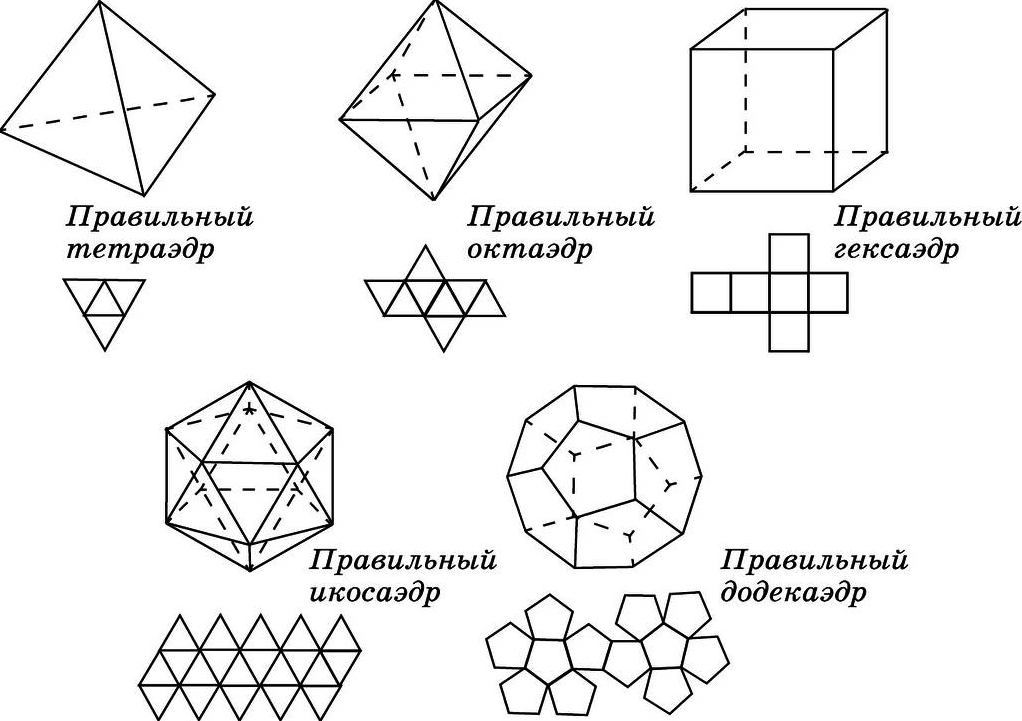 Используя свою фантазию, можно изобразить любую аппликацию из нужных фигур.
Используя свою фантазию, можно изобразить любую аппликацию из нужных фигур.
Полезные советы
Если у вас после покупки электроники или других вещей, остались картонные коробки, не нужно их выбрасывать.
Из картона можно сделать огромное количество поделок как для дома, так и для детей .
Здесь вы сможете узнать, как сделать 5 очень интересных и полезных вещей из картона, а также посмотреть, какие невероятные поделки делают некоторые мастера своего дела.
Гирлянда из картона своими руками
Вам понадобится:
Блестки на платье (пайетки)
Канцелярский нож
Суперклей или горячий клей
Веревка.
1. Нарисуйте на картоне ровные буквы, геометрические фигуры или узоры и вырежьте их.
* Чтобы получить букву на картоне, можно просто использовать линейку и карандаш или можно напечатать на бумаге букву, положить бумагу на картон и канцелярским ножом вырезать букву, обводя ее по контуру.
2. Приготовьте блестки (пайетки) и начните их приклеивать к картону. Можно использовать разные виды пайеток и не обязательно, чтобы пайетки были на нитке.
3. Когда все буквы или фигуры готовы, положите их на ровную поверхность задом наперед и в обратной последовательности и приклейте к ним нить.
Когда клей высохнет, гирлянду можно вешать.
Как сделать из картона органайзер для рабочего стола
Вам понадобится:
25 листов картона (25 х 25 см)
Линейка
Карандаш
Канцелярский нож
Кисточка для клея (при необходимости).
1. Используя линейку и карандаш, начертите на одном листе картона места, где вы хотите сделать углубления (для ручек, мелочей и т.д.), оставляя от края картона минимум 2,5 см.
2. Положите готовый лист картона на новый лист, обведите места, где вы сделали отверстия и вырежьте их из нового листа.
3. Повторяйте те же действия с другими листами, но в конце оставьте 5 листов нетронутыми.
4. Начните аккуратно и ровно склеивать между собой все листы с отверстиями. Для нанесения клея можете использовать кисточку. Можете сначала склеить 5 листов, потом еще пять и так до конца.
5. Склейте между собой 5 нетронутых листов, чтобы сделать дно органайзера.
6. Теперь осталось приклеить дно органайзера к вырезанной части из 20 листов.
Пусть поделка высохнет за ночь и потом можно ее использовать.
Поделки из картона своими руками: геометрическая лампа
Вам понадобится:
Тонкий картон
Ножницы
Канцелярский нож
Клее ПВА или горячий клей
Линейка, циркуль и карандаш (чтобы нарисовать пятиугольник)
Светодиодная лампочка (важно, чтобы была именно LED лампочка, чтобы не сжечь картон)
Патрон лампы.
1. Начните рисовать на картоне пентагоны (фигура с 5-ю одинаковыми сторонами). Для начала вам нужно 11 штук, позже еще примерно 10. В данном примере размер стороны каждого пятиугольника — 6 см, но вы можете выбрать другой размер, главное, чтобы все фигуры были одного размера.
Как нарисовать пентагон (видео)
Чтобы нарисовать ровный пятиугольник, посмотрите вот это видео:
Когда вы нарисовали и вырезали из картона пентагон, используйте его как шаблон, чтобы обводить и вырезать остальные пентагоны.
2. Внутри каждого из 11 пентагонов нарисуйте 5 более мелких пентагонов. В данном примере расстояние между ними — примерно 6 мм.
3. С помощью канцелярского ножа вырежьте все фигуры из каждого картонного пентагона (см. изображение). Это самый длительный процесс, но он довольно простой.
4. Начинаем собирать детали.
Приготовьте одну группу из 5-и пентагонов. Самый большой положите на стол, а следующий по размеру приклейте поверх него так, чтобы его концы касались сторон большого пентагона. Продолжайте в том же стиле, пока не приклеите все детали.
5. Повторите 4 шаг с остальными группами пентагонов.
6. Собираем лампу.
Когда все детали собраны, можно собирать лампу. Положите на ровную поверхность одну деталь и начните приклеивать к ее сторонам остальные детали. Старайтесь клеить так, чтобы рядом находящиеся детали также имели склеенные стороны (см. изображение).
* Вам придется немного приподнимать фигуры. У вас получится, что-то похожее на вазу.
7. Теперь нужно сделать основу для лампы. Для этого нужно нарисовать еще несколько пентагонов (в данном примере их 8 штук) и вырезать их.
Внутри каждой фигуры нарисуйте еще один пентагон (1 см от края) и вырежьте его. Уберите вырезанную часть и аккуратно склейте между собой все остальные детали.
8. Для лампочки нужно вырезать еще один пентагон и сделать в нем отверстие для патрона лампы.
9. Приклейте деталь из 8 шага к основе лампы.
10. Прикрепив лампочку к основе, поставьте лампу так, как она должна стоять (на основу) и сделайте небольшой надрез (или отверстие) для кабеля. Можно добавить немного клея, чтобы лучше прикрепить основу к лампе.
Настенная декорация из картона своими руками (схема)
Вам понадобится:
Ножницы
Карандаш и линейка (чтобы нарисовать несколько квадратов)
Краска акриловая или спрей.
1. Разрежьте картон (картонную коробку) на несколько квадратов разных размеров.
2. Покрасьте все квадраты. В данном примере использовался цвет металлик.
3. Приготовьте большой лист картона и покрасьте его.
4. Начните красить все остальные квадраты и приклеивать их к большому листу.
* Клейте, как вам больше нравится.
5. Можете приклеить работу на стену с помощью двухстороннего скотча или просто поставить ее на полку у стены.
Мебель из картона своими руками: полка в виде облачка
Вам понадобится:
Несколько листов картона
Канцелярский нож
Карандаш
Ножницы.
После текстовой инструкции можно найти видео-инструкцию по созданию данной полки.
1. Возьмите один лист картона и нарисуйте на нем облако. Лучше рисовать так, чтобы одна сторона листа картона служила нижней частью облака (см. изображение).
2. Вырежьте ножницами ваше облачко.
3. Используйте картонное облако, чтобы сделать еще несколько таких же заготовок — обводите его на каждом листе и вырезайте.
* В данном примере использовалось 23 листа картона — 3 листа будут повторять форму облака и 20 будут находиться «внутри» картонной структуры и они имеют похожую структуру, но в них можно сэкономить картон (см. видео).
4. Нарежьте неиспользованный картон на небольшие кусочки, которые нужно приклеивать между деталями облака
5. Начните склеивать аккуратно и по очереди все детали полки, не забывая между деталями приклеивать кусочки картона (см. картинку).
6. Чтобы повесить полку, сначала нужно прикрепить один крючок и один гвоздик (см. видео) и повесить на них полку.
Как сделать полку из картона (видео)
Люстра из картона своими руками (фото)
Поделки из бумаги и картона: зеркало, украшенное картонными деталями
Все маленькие детали сделаны из картонного рулона от бумажных полотенец или туалетной бумаги.
Сначала нужно разрезать рулон на кольца одинаковой толщины, а мотом эти кольца придавить. Из полученных деталей можно сделать красивые украшения и поделки.
Для знакомства с цветами и формами, а также для развития мышления и воображения с детьми можно заниматься созданием аппликаций из геометрического материала. Эти занятия хороши не только тем, что они позволяют детям развиваться и познавать мир, но и доступностью самих материалов. В этой статье мы расскажем, как сделать разные аппликации из геометрических фигур.
Аппликация: домик из геометрических фигур
«Дом». Аппликация для самых маленьких
Аппликации для маленьких детей должны быть максимально простыми и состоять из небольшого числа деталей.
Для создания детской аппликации в виде домика из геометрических фигур нам понадобятся:
- шаблоны для вырезания фигур;
- картон с нанесенным на него изображением итоговой картинки;
- цветная бумага;
- клей;
- ножницы;
- кисточка.
Аппликация «Большой дом»
После того, как ребенок освоил простые аппликации можно переходить к сложным. Чтобы ребенку первое время было проще самостоятельно создавать большие аппликации, необходимо распечатать готовые шаблоны на плотной бумаге.
Шаблоны обычно состоят из двух частей. На одной нанесен контур рисунка, а на второй сами геометрические фигуры, которые необходимо приклеить по контурам.
Аппликация: машина из геометрических фигур
У мальчиков большой интерес вызывают машинки из геометрических фигур. Сами фигуры для создания аппликаций детьми старшего возраста вырезаются самостоятельно, а маленьким детям нужно давать уже вырезанные заготовки.
Аппликация: животные из геометрических фигур
Аппликации животных из геометрических фигур делать не менее увлекательно, но маленьким детям понадобится помощь взрослых, так как состоят они из большого числа деталей. Принцип аппликации таков, как и в предыдущих мастер-классах.
Аппликация: цыпленок из геометрических фигур
Аппликации можно не просто клеить, но и обыграть этот процесс. Для того чтобы сыграть в увлекательную для малышей игру нам понадобятся:
- цветной картон;
- ножницы;
- фломастеры или краски;
- клей;
- кисточка.
- На листе белого картона рисуем основные контуры: солнце, курицу и цыплят, а также прорисовываем травку и облака.
- Из картона соответствующих цветов вырезам курицу, солнце и четыре желтых круга, которым предстоит стать цыплятами.
На стол выкладываем лист картона с нарисованными контурами и деталями и начинаем представление для ребенка:
«Вышла курочка гулять, свежей травки пощипать,
А за ней ребятки — желтые цыплятки.
Солнце по небу гуляло и за тучку забежало
(прокатываем по картинке солнце и убираем его).
Наступила темнота, не ходи за ворота:
Кто на улицу попал – заблудился и пропал
(убираем фигурки цыплят).
Оглянулась курочка, а цыпляток не видно.
Стала курочка звать солнышко
«Выйди, солнышко, скорей! Мне без солнышка обидно –
И цыпляточек не видно!»
Ребенку предлагается «найти цыплят», приклеив их к картону.
Схемы модульных оригами — Леди шик
Величайшее изобретение человечества – бумага, появилась на Востоке. Там же стали сделали первые бумажные фигурки. Орига́ми переводится с японского, как «сложенная бумага». Это древнейшее искусство складывать самые различные фигурки из бумаги. Умельцы оригами обычный лист бумаги могут с легкостью превратить в прекрасного лебедя, журавлика, слоненка или тигренка.
Отдельное направление в искусстве оригами — модульное оригами. Это особая техника создания из бумаги объемных фигур.
Используя схемы модульных оригами можно сделать множество моделей. Собираются фигуры подобно конструктору из небольших модулей.
Для создания модульного оригами нужна бумага, ножницы или канцелярский нож и терпение. Для больших моделей потребуется много маленьких модулей.
Модули делают из прямоугольных кусков бумаги. Размеры бумаги могут быть 53 на 74 мм или 37 на 53 мм. Готовые модули — треугольной формы.
Чтобы получить прямоугольную заготовку складываем стандартный лист А4 по длинной и короткой стороне на 4 части, получаем 16 частей. Если длинная сторона делится на восемь частей, а короткая – на четыре, то получится 32 прямоугольные заготовки.
Из подготовленных прямоугольников складываются модули. Прямоугольник складывается пополам по длинной стороне. Затем — пополам по короткой стороне. Затем разворачиваем его, берем в руки, располагая вторым сгибом к себе.
Края сгибаем к середине — получается треугольник. Переворачиваем его, поднимаем края вверх, уголки загибаем на обратную сторону.
Этот треугольник необходимо перевернуть. После этого отворачиваем уголки и складываем по линиям сгиба, заворачивая их за треугольник. Складываем его пополам.
Полученный модуль используется во всех схемах распространенных модульных оригами.
В зависимости от способа соединения модулей можно получить различные конструкции.
Схемы распространенных модульных оригами бывают трехмерными или плоскими. По плоским схемам собираются всевозможные звездочки, кольца, подставки, вертушки.
С помощью одной из схем распространенных модульных оригами собирается кусудама – объемная,шарообразная гирлянда, состоящая из множества бумажных цветов. В древней Японии кусадамы использовали для излечения больных. Внутрь фигурки помещали лечебные травы и фигура находилась над кроватью больного.
Схемы распространенного модульного оригами позволяют собирать объемные фигуры лебедей и павлинов, кактусов и елочек, различных сооружений, храмов, цветов, подвижных кубиков, модульных колец и многое, многое другое.
Леди шик
Модель многогранника из бумаги. Схемы геометрических фигур
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура — ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Одной из простейших бумажных кусудам считается додекаэдр-оригами. Но это не значит, что он выглядит неэффектно, особенно когда речь идёт о звёздчатой разновидности. Декоративный многогранник, подобно другим своим родственникам – кусудамам, отлично подходит для праздничного украшения помещений или в качестве оригинального подарка. Мини-додекаэдры можно использовать как модные украшения, сделав из них серьги или кулон.
Ажурная модель
Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.
Пошаговая инструкция:
- Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
- Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
- Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
- Складываем фигуру по диагонали, как показано на рис 4.
- Модули для додекаэдра-кусудамы готовы.
Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.
Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.
Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.
За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.
Подробная сборка ажурного додекаэдра представлена и в видео-МК:
Кусудама из правильных пятиугольников
Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.
Пошаговая инструкция:
- Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
- Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
- Аналогично складываем противоположные углы.
- Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
- Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
- Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
- Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
- Продолжаем сборку, пока не используем все 12 модулей.
Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.
Додекаэдр-звезда
Правильные звёздчатые многогранники относятся к самым красивым геометрическим фигурам. С момента своего открытия в XVI веке, они считались символом совершенства Вселенной. Малый звёздчатый додекаэдр впервые построил немецкий астроном и математик Иоганн Кеплер – создатель знаменитой теории о строении Солнечной системы. Многогранник имеет собственное имя: Арур Кэли, в честь английского учёного, сделавшего огромный вклад в развитие линейной алгебры.
Малый звёздчатый додекаэдр-оригами представляет собой фигуру из 12 граней-пентаграмм, с пятью пентаграммами, сходящимися к вершинам. Он состоит из 30 модулей, которые складываются из квадратов, размером 8х8 см. Лучше всего использовать профессиональную бумагу-оригами, которая позволит создавать чёткие грани и жёсткие узлы, не позволяющие конструкции распадаться или деформироваться.
Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.
Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.
Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.
Игрушки древних римлян
На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.
Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.
В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.
Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.
Здесь уже публиковались модели многогранников (http://master.forblabla.com/blog/45755567715/Mnogogranniki), но хочется добавить свои. Ссылка та же, на wenninger.narod.ru. У меня сначала появилась книга, потом, когда подключился к интернету, написал даже письмо автору и получил ответ, потом книга с письмом потерялись, но нашёл сайт и продолжил делать модели.
Если интересно, могу каждый сфотографировать отдельно.
Александр
Ну что ж, по просьбе трудящихся выкладываю фото всех многогранников. Названия я особо не помню, я их классифицирую по многогранному углу. В книге (Веннинджер. Модели многогранников) собраны как многогранники, так и их звёзчатые формы. Платоновы тела это 5 выпуклых правильных многогранников. У них грани одного типа (правильные треугольники, квадраты и пятиугольники) и все многогранные углы одинаковы. Архимед добавил ещё 13 выпуклых полуправильных многогранников (грани — разные многоугольники, но все углы по-прежнему одинаковы). А вот если брать не выпуклые многоугольники (в книге используются треугольники, квадраты, пятиугольники, восьмиугольники и десятиугольники), а их звёздчаные формы (пятиугольная, восьмиугольная и десятиугольная звезды), то получается масса новых многогранников. К тому же, грани могут соединяться также в виде звёзд, поэтому невыпуклые многогранники могут состоять, как из звёздчатых многоугольников, так и из выпуклых.
Наконец, аналогично тому, что продолжение линий превращает выпуклый многоугольник в звёздчатый, так и продолжение граней образует звёздчатые формы. Правда, известно только 4 правильных многогранников такого типа (все три звёздчатые формы додекаэдра и одна звёздчатая форма икосаэдра), у других либо грани — неправильные многоугольники, либо многогранник распадается на несколько отдельных многогранников.
Особую красоту дают формы, у которых грани видны с двух сторон, а также содержащие дыры, плюс те, части которых только касаются друг друга вершинами.
Конечно, у многогранников есть своя математика, но об этом потом.
Фото сопровождаются моделями многогранных углов. Это основание пирамиды, которая получится, если от вершины многогранника отрезать кусочек, как от торта. 3, 4, 5, 6, 8 и 10 обозначают выпуклые многоугольники, 5/2, 8/3 и 10/3 — пятиугольную, восьмиугольную и десятиугольную звезду (последовательность вершин делает соответственно 2, 3 и 3 оборота вокруг центра).
Поехали. Сначала треугольники. (в скобках — номера моделей из книги).
Бесконечное семейство призм.
Треугольная призма.
Черырёхугольная призма, гексаэдр, куб (3).
Пятиугольная призма и её звёздчатая форма.
Шестиугольная призма.
Тетраэдр (1).
Додекаэдр (5) и три его звёздчатые формы, которые являются правильными многогранниками: малый звёздчатый додекаэдр (20), большой додекаэдр (21) и большой звёздчатый додекаэдр (22):
Усечённый тетраэдр (6).
Усечённый октаэдр (7).
Усечённый гексаэдр (куб) (8).
Усечённый икосаэдр (9). Раньше так шили футбольные мячи.
Усечённый додекаэдр (10).
Ромбоусечённый кубооктаэдр (15).
Ромбоусечённый икосододекаэдр (16).
Квазиусечённый гексаэдр (92).
Квазиусечённый кубооктаэдр (93).
Большой квазиусечённый икосододекаэдр (был. Увы, изнутри был непрочным и однажды сломался). (108)
Переходим к многогранникам, у которых в угле сходится 4 грани.
Сначала вершинная фигура в виде квадрата.
Бесконечное семейство антипризм.
Треугольная антипризма, октаэдр (2), и его звёздчатая форма — звёздчатый октаэдр (19).
Квадратная антипризма и её две звёздчатые формы.
Кубооктаэдр (11) и его звёздчатые формы (43 — 46).
Икосододекаэдр (12) и его звёздчатые формы (47, 63, 64), а в книге их очень много.
Ромбокубооктаэдр (13) и его звёздчатая форма.
А вот этот многогранник (псевдоромбокубооктаэдр) наделал много шума, т.к. его опубликовали только спустя 2000 лет после Архимеда (на рубеже 50-60 г.г. 20-го века). На самом деле, у него есть дефект: когда я говорил, что у полуправильных многогранников углы (вершинная модель) одинаковые, то можно заметить, что порядок обхода граней у соседних вершин всегда зеркальный, например, если у одной вершины грани идут в порядке 3-4-4-4 по часовой стрелке, то у соседней вершины тот же порядок, но против часовой стрелки. Так вот, у псевдоромбокубооктаэдра встречаются пары вершин, у которых нет зеркальной симметрии.
Ромбоикосододекаэдр (14).
Малый икосоикосододекаэдр (71).
Додекододекаэдр (73).
Ромбододекододекаэдр (76).
Большой икосододекаэдр (94).
Большой додекоикосододекаэдр (99).
Теперь многогранники, у которых тоже 4 грани сходятся в одной вершине, но порядок крест-накрест:
Тетрагемигексаэдр (67).
Октагемиоктаэдр (68).
Малый кубокубооктаэдр (69).
Много интересного можно найти для себя в тех сферах науки, которые, казалось бы, никогда не пригодятся в привычной жизни простого обывателя. Например, геометрия, о которой большинство забывают, только лишь переступив порог школы. Но странным образом малознакомые области науки становятся очень увлекательными, если с ними столкнуться поближе. Вот и геометрическая развертка многогранника — совершенно ненужная в повседневной жизни вещь — может стать началом увлекательного творчества, способного захватить и детей, и взрослых.
Красивая геометрия
Украшать интерьер дома, создавая своими руками необычные, стильные вещи, — это увлекательное творчество. Смастерить самостоятельно из плотной бумаги различные многогранники — значит создать уникальные вещи, которые могут стать просто занятием на день или два, а могут превратиться в дизайнерские интерьерные украшения. К тому же с развитием техники, способной к пространственному моделированию всевозможных вещей, стало возможным создание стильных и современных 3D-моделей. Есть мастера, которые при помощи простроения разверток по законам геометрии делают из бумаги макеты животных и различных предметов. Но это достаточно сложное математическое и чертежное творчество. Начать работать в подобной технике поможет
Разные грани — разные формы
Многогранники — это особая сфера геометрии. Они бывают простые — к примеру кубики, которыми дети играют с раннего возраста, — а бывают очень и очень сложные. Простроение развертки многогранников для склеивания считается достаточно сложной областью конструирования и творчества: нужно не только знать основы черчения, геометрические особенности пространства, но и иметь пространственное воображение, позволяющее оценить правильность решения еще на стадии проектирования. Но и одной фантазией не обойтись. Чтобы сделать развертки не достаточно просто представить, как в конце концов должна выглядеть работа. Нужно уметь правильно ее просчитать, сконструировать, а также грамотно начертить.
Самый первый многогранник — кубик
Скорее всего, каждый человек, посещавший школу, еще в начальных классах сталкивался на уроках труда с работой, результатом которой должен был стать бумажный кубик. Чаще всего учительница раздавала заготовки — развертки многогранника куба на плотной бумаге со специальными кармашками, предназначенными для склеивания граней модели в единое целое. Такой работой ученики начальной школы могли гордиться, ведь при помощи бумаги, ножниц, клея и своих усилий получалась интересная поделка — трехмерный куб.
Занимательные грани
Удивительно, но многие знания об окружающем мире становятся интересны не на школьной скамье, а лишь тогда, когда можно найти в них нечто увлекательное, способное дать что-то новое, необычное в привычной жизни. Не многие взрослые помнят, что те же многогранники делятся на огромное количество видов и подвидов. Например, есть так называемые платоновы тела — выпуклые многогранники, состоящие только лишь из Таких тел всего пять: тетраэдр, октаэдр, гексаэдр (куб), икосаэдр, додекаэдр. Они представляют собой выпуклые фигуры без впадин. Звездчатые многогранники состоят из этих основных фигур в различных конфигурациях. Поэтому-то развертка многогранника простого позволяет нарисовать, вернее начерить, а затем и склеить из бумаги звездчатый многогранник.
Правильные и неправильные звездчатые многогранники
Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников — красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра — сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.
Красота в простоте
Все объемные тела, построенные по законам геометрии, будут смотреться завораживающе, в том числе и звездчатый многогранник. Развертка каждого элемента любого подобного тела должна быть выполнена максимально точно. И даже самые простые объемные многогранники, начиная с платонового тетраэдра, — удивительная красота гармонии мироздания и труда человека, воплощенного в бумажной модели. Вот, допустим, самый многогранный из платоновых выпуклых многогранников — додекаэдр. В этой геометрической фигуре 12 абсолютно одинаковых граней, 30 ребер и 12 вершин.Чтобы сделать развертки правильных многогранников для склеивания, нужно приложить максимум аккуратности и внимательности. И чем крупнее фигура по размерам, тем точнее должны быть все измерения.
Как построить развертку самостоятельно?
Пожалуй, помимо склеивания многогранника — хоть звездчатого, хоть платоновского, — еще интереснее построить развертку будущей модели собственными силами, оценив свои способности к черчению, конструированию и пространственному вообжению. Простые платоновсткие тела состоят из простых многоугольников, которые в одной фигуре идентичны друг другу. Так, тетраэдр — это три равнобедренных треугольника. Прежде чем простроить развертку, нужно представить себе, как правильно сложить плоские многоугольники между собой, чтобы получить многогранник. Треугольники можно соединить между собой по ребрам, прочертив один рядом с другим. Для склеивания развертки многогранников схемы должны быть снабжены специальными кармашками или клапанами, которые позволят соединить все части в единое целое. Тетраэдр — простейшая фигура из четырех граней. Октаэдр можно представить как двойной тетраэдр, у него восемь гарней — равнобедренных треугольников. Гексаэдром называют знакомый всем с детства куб. Икосаэдр представляет собой соединение 20 равнобедренных треугольников в правильный выпуклый многогранник. Додекаэдр — это объемная фигура из 12 граней, каждая из которых представляет собой правильный пятиугольник.
Тонкости работы
Построить разверту многогранника и склеить из нее бумажную модель — дело тонкое. Развертку, конечно, можно взять уже готовую. А можно, приложив услилия, построить ее самостоятельно. Но чтобы сделать полноценную объемную модель многогранника, нужно ее собрать. Многогранник лучше всего делать из плотной бумаги, которая хорошо держит форму и не коробится от клея. Все линии, которые необходимо согнуть, лучше всего предварительно продавить, используя, например, непишущую шариковую ручку или обратную сторону лезвия ножа. Этот нюанс поможет сложить модель аккуратнее, с соблюдением размеров и направлений ребер.
Если сделать разные многогранники из цветной бумаги, то такие модели можно использовать в качестве декоративных элементов, украшающих помещение — детскую комнату, кабинет, гостиную. Кстати, многогранники можно назвать уникальной находкой декораторов. Современные материалы позволяют на основе геометрических фигур создавать оригинальные предметы интерьера.
Создавать поделки своими руками интересно не только детям, но и взрослым. Однако для взрослых придумано достаточное количество моделей, которые отличаются сложностью выполнения и временем, затраченным на их создание. В последнее время у взрослых и детей появился интерес к созданию сложных геометрических фигур. К такому виду фигур относится икосаэдр, который представляет собой правильный многоугольник и является одним из платоновых тел – правильных многогранников. Эта фигура имеет 20 треугольных граней (равносторонних треугольников), 30 ребер и 12 вершин, которые являются местом стыка 5 ребер. Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда. Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.
Предлагаем вам несколько вариантов разверток икосаэдра, которые можно распечатать, перенести на плотную бумагу и картон, согнуть по линиям и склеить.
Как сделать икосаэдр из бумаги: схема
Для того чтобы собрать икосаэдр из листа бумаги или картона, необходимо предварительно подготовить следующие материалы:
- макет икосаэдра;
- клей ПВА;
- ножницы;
- линейка.
Во время создания икосаэдра важно обратить особое внимание на процесс сгиба всех деталей: для того, чтобы ровно согнуть бумагу, можно использовать обычную линейку.
Примечательно, что икосаэдр можно встретить и в повседневной жизни. Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч. Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч.
Такой футбольный мяч можно сделать самостоятельно, распечатав предварительно развертку усеченного икосаэдра в 2 экземплярах:
Создание икосаэдра своими руками представляет интересный процесс, который требует вдумчивости, терпения и большого количества бумаги. Однако результат, полученный в итоге, будет радовать глаз еще долгое время. Икосаэдр можно дать поиграть ребенку, если он достиг уже трехлетнего возраста. Играя с такой сложной геометрической фигурой, он будет развивать не только образное мышление, пространственные навыки, но и знакомиться с миром геометрии. Если же взрослый решил создать икосаэдр самостоятельно, то такой творческий процесс по конструированию икосаэдра позволит скоротать время, а также похвастаться перед близкими своим умением создавать сложные фигуры.
Геометрические фигуры объемные схемы шаблоны. Геометрические фигуры из бумаги своими руками с описанием и фото схем
Оригами открывает невероятные широты для фантазии и творчества. Мастера из бумаги научились делать самые разнообразные поделки. Это разные животные, птицы да даже растения. Но сегодня мы подробно рассмотрим, как делать геометрические фигуры быстро и легко из бумаги.
Такие фигуры помогут развить представление о трёхмерных фигурах, а также общее представления о них. Лучше всего они подойдут тем, у кого возникают сложности с тригонометрией, так как этот раздел геометрии требует очень хорошего визуального представления разных фигур.
Изучаем пошагово принцип изготовления геометрических фигур из бумаги
Оригами в большинстве случаев заключается в складывании разнообразных форм из бумаги. В нашем же случае будет похоже, но немного иначе.
Схема или как её ещё называют развёртка – является обязательным элементом при изготовлении любой геометрической фигуры. Схема представляет собой двухмерное изображение «развёртки» нашей фигуры на бумаге. Представим куб. И мы развернули его, что в итоге получилось? Столбик из четырёх одинаковых квадратов и два таких же квадрата сбоку. Своеобразная буква «Т».
После того, как вы сделали или нашли развёртку, вам необходимо сложить её в фигуру и очень аккуратно проклеить все элементы.
Без развёртки невозможно сделать ни одной правильной геометрической фигуры, которая была бы максимально ровная и не содержала бы погрешностей. В интернете можно найти огромное количество разнообразных схем, для самых разных фигур. Мы же рассмотрим в качестве примера изготовление цилиндр и шляпу.
Солидный цилиндр.Цилиндр является одной из самых простых фигур в оригами. С его изготовлением справится даже новичок. И так, приступим к первому нашему творению.
Для начала ищем или делаем сами схему. Схема цилиндра представляет собой прямоугольник, длина которого вычисляется по формуле 2ПиR, где R – это радиус вашего цилиндра, то есть если вы хотите получить цилиндр диаметром 10 сантиметров, то его радиус будет равен пяти. И тут же обратная зависимость: если вы уже нарисовали прямоугольник, длинной, например, 40 сантиметров, то радиус окружности соответственно будет равен 40/2Пи. Примерно 6,2 сантиметра.
На схеме, проводим аккуратную линию ровно по центру прямоугольника. Продолжаем нашу линию за его стороны, то есть, линия должна пересекать прямоугольник. Дальше мы должны точно знать диаметр цилиндра, чтобы вычислить радиус окружности, если же вы сначала нарисовали прямоугольник, то пользуйтесь формулой l/2Пи, где l – длина вашего прямоугольника. После того, как вы определили радиус, берём циркуль и размещаем на пересечении нашей линии симметрии и стороны прямоугольника. Начинам образно проводить окружность и смотрим, где будет вторая точка пересечения с линией симметрии, она должна находиться за пределами прямоугольника. Именно эта точка и будет центром окружности. Повторяем действия с другой стороны. Наша поделка, например, делалась по такой схеме:
Если же вы нашли схему в интернете, то достаточно распечатать её. И вырезать её.
После того, как мы вырезали её, необходимо перейти к её складыванию. Начинаем складывать наш цилиндр с его основной части. Для этого сворачиваем в трубочку прямоугольник. Сворачиваем сразу с двух концов, то есть, берём один конец прямоугольника и другой, и тянем их друг к другу. Что бы получилась своеобразная труба, у которой «открыты» два кружочка.
Потом загибаем оба «окошка» внутрь и меняем по необходимости толщину трубочки, что бы эти окошки идеально вошли внутрь. Потом склеиваем получившийся цилиндр.
Шляпа из бумаги.Шляпа – такой же цилиндр, но у него нижнее окно будет открыто на во внешнюю сторону. Нам потребуется картон, ножницы, тарелка, клей . Начнём!
Для начала разрезаем лист картона на две полосы, ширина которых будет равна высоте цилиндра.
Длина полосок будет зависеть от того, какого диаметра вы хотите получить шляпу. Если вы хотите одевать шляпу на голову, то следует измерить обхват головы и полученное число поделить на два.
Склеиваем детали так, чтобы получить единую длинную полосу.
Сворачиваем полосу в цилиндр и скрепляем его.
Выбираем, по вашему вкусу, одну из круглых сторон и делаем на ней ровные надрезы, глубина которых равна двумя сантиметрам. Отгибаем получившиеся лепестки и откладываем цилиндр в сторону.
Берём ещё небольшой кусочек картона и обводим, заготовленную ранее, тарелку. В центр получившейся окружности поставьте ваш цилиндр и обведите его. Вырезаем из листа сначала большую окружность, а потом маленькую. В итоге мы должны получить кольцо.
Ставим цилиндр на устойчивую, ровную поверхность вниз лепестками и к каждому из них приклеиваем кусочки двухстороннего скотча.
Шляпа готова!
Небольшая подборка видео по теме статьи
Те, кто любит бумажные изделия, могут использовать их в оформлении комнат и дизайне интерьера, чтобы не тратить много денег. Бумажные поделки могут создавать уникальные и очень стильные домашние интерьеры.
- уникальной мебели;
- привлекательных украшений на стены;
- осветительных приборов;
- зеркал;
- рамок для картин;
- оконных штор;
- декоративных ваз.
Бумага — материал, который имеет несколько применений, с ним легко работать, он является экологически чистым, дешевым.
Бумажная домашняя обстановка и настенные украшения напоминают произведения искусства, вдохновленные оригами, тем самым добавляя невероятные детали в современный дизайн интерьера, декорирование. Поэтому, вместо того, чтобы уничтожать ненужную бумагу подумайте о том, чтобы превратить ее в предмет искусства и интерьера.
Вы будете поражены тем, насколько обычная бумага способна трансформировать ваше пространство.
Идеи дизайна и поделки
Идеи дизайна интерьера, сделанные из бумаги, такие как настенные украшения или светильники, имеют возможность существенно преобразить, украсить ваш интерьер. Различные объемные и фантастические 3D формы для украшения стен, потолка , лестниц, домашней мебели могут тоже быть сделаны из бумаги.
Имея нежный эксклюзивный вид, бумажные изделия добавляют прекрасные акценты на :
- люстры;
- настольные лампы;
- рамы и двери;
- оконные шторы;
- декоративные вазы.
Украшения могут быть в виде:
- бумажных цветов;
- птиц;
- бабочек.
Они придадут романтический и интересный штрих. Бумажные изделия производят в дизайне интерьера разный эффект, в зависимости от задумки – он может быть необычный, удивительный или красивый, впечатляющий, стильный, современный или ретро современный.
Дизайн с бумажными цветами выглядит удивительно сказочно. Они выглядят как красивые произведения искусства, которые вдохновляют перерабатывать бумагу, оформлять интерьер в экологически чистом стиле.
Для этого можно разбавить этот естественный материал с традиционным кирпичом, древесиной, производя бумажные конструкции на стенах и потолке.
Меняйте свой дизайн стен, потолка каждый год, чтобы ваш декор всегда выглядел свежим, используя бумагу для современного дизайна интерьера, декора стен и уникальных потолочных конструкций. Есть много идей, мест и предметов, где этот тренд может быть использован.
Поэтому, если вы являетесь энтузиастом по ручному труду, то почему бы вам не попробовать свои силы на бумаге для отделки дизайна? Для дизайнеров интерьера, художников это универсальное средство искусства стало привычным делом и они предлагают для вашего творчества свои наработки.
Но что более важно, не забывайте, что вы делаете больше, чем просто украшения — вы способствуете сокращению утилизации и спасаете окружающую среду от засорения.
Газета — прекрасный материал для работы
Газета — это тот элемент, который становится совершенно бесполезным уже на следующий день после выпуска, а бесконечная рекламная продукция в виде газет в наших почтовых ящиках и подавно наводит на депрессию своей щедростью.
Таким образом, мы всегда используем ее как мусорный объект нашего дома.
Но знаете ли вы, что именно эту макулатуру можно использовать как замечательный компонент для изготовления красивых настенных украшений или красивых предметов домашнего декора!
Мне захотелось подобрать для вас наиболее интересные изделия, которые можно легко выполнить своими руками, именно из газетной бумаги, чтобы совместить приятное с полезным – улучшить экологическую обстановку на планете, сотворить красивое изделие для своего дома. Проверьте – это очень просто.
Настенный декор
- Чтобы сделать шаг за шагом настенную объемную подвеску, сверните в тонкую трубку несколько газет.
- Теперь склейте эти свернутые палочки на картоне, дайте хорошо впитаться клею.
- После этого используйте ножницы, чтобы вырезать какую-либо выбранную фигуру из этих склеенных рулонов бумаги, например, форму сердца или цветочную, или выберите форму куклы.
- Убедитесь, что вы вырезаете объект большого размера идентичный тем, что будут меньшего размера (лучше всего фигуры делать по шаблону).
- Теперь возьмите немного лески с бусинами и сделайте 5 струн разных размеров, прикрепив их основания к бумажной поделке.
- Теперь выберите цвет, в котором будет выполнено изделие, придумайте несколько интересных орнаментов поверх основания, чтобы сделать подвеску более красивой.
Как сделать подарочный пакет
Выбор подарочных пакетов ручной работы с элементами старых газет станет тем решением, которое обнаружит в вас незаурядную смелую личность. Ведь непросто для нашего менталитета сделать подарок в газете, как наши бабушки, дедушки в доперестроечную эпоху. Такое решение не только приводит нас к способу переработки вещей, но, в то же время, исполняет все необходимые требования к транспортировке, обычно предъявляемые упаковке – то есть, это еще весьма хороший вариант.
Чаша Папье-маше
Вы можете также сделать корзину или гигантскую чашу для хранения сухих вещей из ежедневных газет.
Красивый декор
Ваза своими руками
Сверните их плотно как в этом видео, согните в соответствии с требованиями к форме. Одна из самых замечательных свойств этих газет в том, что изделие будет удивительно гибким, поэтому вы сможете создать несколько полезных предметов, скручивая их в соответствии с вашим желанием.
Предметы мебели
Это изделие изготовляется по принципу квиллинга – намотайте скрученные листы газеты на ручку или карандаш с использованием клея, а затем покрасьте их в предпочитаемый цвет. Строительный материал для декоративной вазы готов.
Скручивание газетных листов в жгуты – лучший способ использовать газету для поделок своими руками. С такими трубками вы можете оформить современную цветочную вазу, приклеив полоски горизонтально или вертикально, а также выполнить более сложные фигуры вроде рамы для зеркала, фото или настенных тарелок и т. д.
Ваза ручного изготовления
Хотя сам процесс переработки бумажных отходов может быть весьма сложным, на выходе вы получите прекрасный материал из которого получаются первоклассные открытки. Из такой бумаги можно изготовлять предметы. Эту вазу вы можете изготовить из любой бумаги на ваш вкус.
Пошаговое руководство
- Вам понадобится 12 листов 25 × 25 см. В конце важно правильно собрать элементы. Всегда используйте три элемента для объединения.
- Когда вы сформировали мяч из 12 единиц фигурок, выньте один блок в одном месте.
- Освободившиеся две вкладки складываются и приклеиваются. Повторите ту же процедуру с нижней стороны.
- Если не сдать устойчивое основание снизу, то ваза может перевернуться, поэтому нижнее отверстие также необходимо.
Как сделать тропические бумажные орхидеи
Тропические орхидеи довольно дорогие, но вы можете сделать их из бумаги, ели любите эти цветы, но не хотите тратить свои деньги.
Инструменты, которые вам пригодятся:
- шаблон орхидеи;
- настольный принтер;
- ножницы;
- клей;
- бумага.
ШАГ 1
Распечатайте и вырежьте все лепестки орхидеи, которые указаны в шаблоне, на выбранный цвет.
Затем распечатайте, вырежьте центр орхидеи на вторую цветную бумагу, шаблон листа на зеленую бумагу. Вырежьте два набора лепестков, один центр, два листа для каждого цветка.
ШАГ 2
Используйте край ножниц, чтобы скрутить каждый лепесток и центральную часть. Сложите листья пополам. Заверните каждый лепесток в обратном направлении, чтобы сформировать из них форму чаши. Сверните обе стороны на листьях.
ШАГ 3
Прикрепите каждый слой с помощью горячего клея. Самый большой из трех лепестковых фигур расположен снизу загнутыми лепестками вверх, следом за ним приклейте двухсекционный лепесток в центр и центральную часть поверх двух слоев лепестков.
ШАГ 4
Прикрепите листы, перевернув цветок и установив два листа сзади.
ШАГ 5
Чтобы сделать зажим для волос, браслет или подарочную упаковку, приклейте крепежный элемент к задней части цветка.
ШАГ 6
Прикрепите ствол. Для орхидеи на стебле согните конец проволоки под углом. Вырежьте небольшую листовую фигуру, сделав разрез на одну треть по центру и проведите угол проволоки в эту складку. Приклейте лепесток и проволоку сзади орхидеи.
ШАГ 7
Использовать готовые орхидеи можно не только в декоре, но и для того, чтобы сделать подарок, букет, носить их на свитере или в волосах.
ШАГ 8
Эти орхидеи могут стать прекрасной альтернативой свадебному букету или украшению.
Цветочные гирлянды
Создайте себе игривое настроение с помощью этих простых в изготовлении объемных бумажных цветов.
Вам понадобится:
- клей-пистолет;
- ножницы;
- клей-карандаш;
- декоративная лента;
- цветная бумага.
ШАГ 1
Выберите цвета
Выберите сочетающуюся расцветку, чтобы получилась сбалансированная цветовая схема. Для монохроматического подхода рассмотрите слоистые оттенки и оттенки одного цвета. Для более многоцветного эффекта смешайте вместе те оттенки, которые отличаются контрастностью.
Для более женственного образа, придерживайтесь приглушенных цветов и пастелей, смешанных с нейтральными, такими как темно-коричневый, коричневый или мягкий серый.
ШАГ 2
Сложите пополам
Используйте квадратные листы, так как бутоны роз имеют совершенно круглую форму. Прямоугольные бумаги должны быть обрезаны до квадратного состояния. Первым шагом в этом процессе является сворачивание каждого листа квадратной бумаги пополам.
ШАГ 3
Сложите на четверть
После того, как было все равномерно сложено пополам, сложите ее снова на четверть.
ШАГ 4
Превратите квадрат в круг
Сложив четверть, используйте ножницы, чтобы закруглить край.
ШАГ 5
Разверните круг
Разверните, чтобы открыть форму. Если вам удалось создать идеальную сферу, пришло время перейти к следующему шагу; однако, если результат получился продолговатый или овальный, лучше повторить предыдущий шаг до создания идеального круга.
ШАГ 6
Начиная по внешнему краю и прокладывая путь к центру, вырежьте сплошные круги в спирали.
ШАГ 7
Сформируйте центральную часть цветка
По мере того, как вы достигнете конца круга при разрезании спиралей, оставьте овальный язычок на конце диаметром примерно 2 см. Это часть каждого бумажного бутона, который будет удерживать спирали вместе с клеем.
Вам вполне могут пригодиться в работе геометрические фигуры- куб, конус, цилиндр, призма, шар. Очень хорошо учиться рисовать натюрморт, для начала составив его из простых геометрических фигур. Пробовать ложить штрих по форме предметов также лучше начиная с простых форм- геометрических. В идеале, они должны быть гипсовые. Но есть ли у вас гипсовые конус, циллиндр, куб, шар? Хорошо, если есть. А если нет…. будем выходить из положения вместе и я расскажу как.
Вы можете увидеть ниже примерные чертежи, по которым можно самостоятельно «выкроить» и склеить геометрические фигуры дома. А в качестве
шара вы можете использовать небольшого размера детский мяч, предварительно окрашенный в белый цвет, например- гуашью или эмульсионной краской.
Для начала можете попробовать склеить макеты геометрических фигур из обычной бумаги- ксероксной либо оберточной, которые будут указаны. Можете пока просто потренироваться. Если с макетированием у вас все в порядке, можете выполнять работу сразу начисто. Но учитывая нужные размеры. Допустим: если размеры, указанные вам кажутся малы- стоит увеличить их, дабы и макеты фигур получились не маленькие. Либо даже несколько видоизменить конус или цилиндр- как вам захочется. Чем больше и разных по размеру фигур сделаете, тем больше у вас будет выбор- из чего составлять натюрморт и что рисовать.
1. Итак, для конечной работы нам понадобится плотный лист ватмана, можно взять вместо бумаги картон. Нужно перенести эти чертежи геометрических фигур на бумагу. Вооружитесь карандашом, ластиком, линейкой, транспортиром и циркулем и начинайте неспешно работать над заготовками макетов цилиндра, конуса и куба.
2. После того, как чертежи фигур будут выполнены, делаем следующее: возьмите канцелярский нож и на линиях изгибов сделайте неглубокие надрезы (не прорезая бумагу насквозь!).
3. После этого тем- же канцелярским ножом можно вырезать заготовки с плоскости листа. Все надрезы ножом делаются под линейку! Кривые линии прорезаем старательно вручную или под лекала.
4. Те надрезы, которые вы делали на местах изгибов, позволят вам хорошо согнуть бумагу по краю изгиба, не сминая ее.
5. После всего этого останется только склеить заготовки и у вас получатся свои, собственные геометрические фигуры.
Замечание: если работа получилась грязной, то есть возможность прокрыть фигуры белой краской. Но в этом случае бумагу может «повести» от влаги, если ваша бумага очень рыхлая или тонковата. Для этого, изначально, нужно натягивать бумагу на планшет.
Кстати, такие навыки макетирования вам очень даже пригодятся, если вы захотите учиться, например, на факультете промышленный дизайн. Там умению делать макеты да и самим макетам приделяется очень большое значение, так- что, тренируйтесь, и вырабатывайте аккуратность и усидчивость.
Чертеж макета куба
Для пробного макета куба можно взять в размерах длину грани 10 сантиметров. Для основательной работы, для куба, который вы уже сможете использовать в рисунке можно взять длину грани- 20 см. Естественно, учитывайте, что все углы куба равны 90 градусам, значит удобно при черчении использовать и линейку, и уголок. Чертеж макета куба не сложный, вполне быстро у вас получится и сам его макет. Главное делать все предельно точно: параллельно и перпендикулярно.
Напоминаю: синим показана та часть макета, на которую будет наноситься клей. Эта часть будет загибаться и для чистого, ровного загиба, в последствии- угла макета используйте неглубокие надрезы канцелярским ножом по линии загиба. Кстати, такие кубики, выполненные из цветной бумаги или окрашенные в различные цвета могут использоваться в наблюдениях за поведением цвета в пространстве в цветоведении . Для этого возьмите выполненные вами цветные кубики и подвесьте по середине вашей комнаты или поближе к окну. В течении для иногда поглядывайте на кубики- можно наблюдать, как цвет меняется в течение дня- с утра до ночи, когда освещение меняется или пропадает вовсе. Цвет меняется не только от силы освещения, но и от его качества- утром один оттенок, к обеду кубик приобретает уже другие оттенки; в жаркий день один цвет, в пасмурный- другой; при дневном освещении- один цвет, при искусственном- другой. И все эти градации могут происходить только с одним из ваших кубиков, но ведь их у вас разноцветных может быть несколько!
Чертеж макета конуса
Чертеж макета конуса- радиус круга возьмите пока 5 см. Угол верхушки- 135 градусов. Длина высоты куба- 13,5см. Выполните сначала пробный макет. Если он вас устраивает, то окончательный чистовой макет можно выполнить в два раза больше. Для этого просто увеличьте все размеры в два раза. Если хотите другую форму, то достаточно увеличить высоту самого конуса- увеличьте длину высоты конуса. Этого достаточно.
Чертеж макета пирамиды
Пирамида. Тут все просто. Пирамида у нас равнобедренная, все стороны у нас одинаковы. Размеры можете брать любые, но достаточно и 20см.
Чертеж макета цилиндра
Размеры для черновой работы- радиус окружности равен 3,5см., длина развертки 23,5 см. Что- бы увеличить размеры цилиндра, нужно умножить величины в желаемое количество раз. Достаточно в 2 раза. Можно поэкспериментировать- сделать цилиндр высоким или приземленным, как вам понравится. Для рисунка все пригодится, экспериментируйте, пробуйте.
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательноознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вамразвёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура — ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
This section contains some shortcodes that requries the Jannah Extinsions Plugin. You can install it from the Theme settings menu > Install Plugins.
Вы только начали увлекаться оригами, и ищите поделки для начинающих? А, может, Вам или Вашему ребенку задали поделку по трудам или геометрии, а идей совсем нет? Ищите чем полезным и увлекательным заняться в свободное время с ребенком? Тогда объемные фигуры из бумаги — это отличное решение всех проблем.
Математика, оказывается, тоже может быть интересной, а не только сложной и непонятной. В особенности, геометрия, со всеми ее многогранниками (тетраэдр, куб, октаэдр, додекаэдр, икосаэдр). От самих этих названий становится жутко, а как представить их в реальности, а не на листе бумаги?
Делаем объемные фигуры из бумаги
Как помочь ребенку или человеку, не имеющему никакого представления об этих геометрических фигурах? А ведь это легко, и, более того, процесс ознакомления с азами геометрии может принести массу положительных эмоций и удовольствия. И в этом поможет поделка оригами «геометрические фигуры», а также другие бумажные поделки , которые легко собрать по готовым схемам.
Нам понадобится:
- Ножницы
- Карандаш
- Картон (цветной, или любая плотная бумага)
- Принтер (для того, чтобы распечатать готовые макеты)
Для того, чтобы гирлянда была яркой и радужной, определите цвет для каждого элемента. Используя готовые макеты, подготовить заготовки для последующей работы.
Скачать шаблоны-заготовки:
- Двадцатигранник
Аккуратно вырезать заготовки и с помощью клея (лучше всего использовать клей-стик, так как с ним практичней работать — он не растекается, и с таким клеем удобно работать детям) склеить все фигуры.
Пройтись по всем швам, закрепляя все стыки, чтобы швы не разошлись и сошлись ровно.
Вот и все, объемные фигуры из бумаги готовы. Согласитесь, что наглядно намного легче объяснить, что такое тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Этот вариант отлично подойдет для детей, которые только начинают свое знакомство с геометрией.
Оценка разницы объемов зарегистрированных трехмерных дооперационных и послеоперационных стоматологических данных КТ
Dentomaxillofac Radiol. 2012 May; 41 (4): 328–339.
TL Economopoulos
1 Школа электротехники и вычислительной техники, Афинский национальный технический университет, Греция
PA Asvestas
2 Кафедра технологии медицинских инструментов, Технологический образовательный институт Афин, Греция
GK Matsopoulos
1 Школа электротехники и вычислительной техники, Национальный технический университет Афин, Греция
B Molnár
3 Кафедра пародонтологии, Университет Земмельвейса, Будапешт
P Windisch
3 Университет Пародонтологии Семмелвейс , Будапешт
1 Школа электротехники и вычислительной техники Афинского национального технического университета, Греция
2 Кафедра технологии медицинских инструментов, Афинский технологический образовательный институт, Греция
3 Кафедра пародонтологии, Земмельве is University, Budapest
Professor George K. Matsopoulos, 9, Iroon Polytechniou str, Zografos, 15780 Athens, Greece.Электронная почта: rg.autn.ece.dse@ostamgПоступила в редакцию 14 февраля 2011 г .; Пересмотрено 30 мая 2011 г .; Принята к печати 31 мая 2011 г.
Copyright 2012 Британский институт радиологии Эта статья цитируется в других статьях в PMC.Abstract
Цель: Цель этого исследования — предложить полную методологию для автоматической регистрации трехмерных (3D) дооперационных и послеоперационных стоматологических объемов с помощью компьютерной томографии, а также предоставить набор инструментов для количественной оценки и оценки их объемные различия.
Методы: Предложенная методика была применена к данным конусно-лучевой компьютерной томографии (КЛКТ) от 20 пациентов с целью оценки объема увеличенной кости в альвеолярной области. В каждом случае дооперационные и послеоперационные данные регистрировались с использованием трехмерной аффинной схемы. Эффективность алгоритма 3D-регистрации оценивалась путем измерения среднего расстояния между краями зарегистрированных наборов. Различия между зарегистрированными наборами оценивали с помощью 3D-рентгенографии с вычитанием.Объем различий был окончательно оценен путем определения интересующих областей в каждом срезе вычтенных трехмерных данных и путем объединения всех соответствующих срезов для моделирования желаемого интересующего объема. Эффективность алгоритма была проверена путем его применения к нескольким эталонным объектам стандартной формы с известными объемами.
Результаты: Удовлетворительное выравнивание было достигнуто, поскольку между краями зарегистрированных наборов было зафиксировано небольшое среднее смещение 1,483 ± 1,558 мм.Более того, оцененные объемы близко соответствовали объемам эталонных объектов, использованных для проверки, поскольку зарегистрированные различия объемов были менее 0,4 мм 3 во всех случаях.
Заключение: Предлагаемый метод позволяет автоматически регистрировать наборы данных 3D КЛКТ и объемно оценивать их различия в конкретных областях интереса. Предлагаемый подход обеспечивает точные объемные измерения в трех измерениях, требуя минимального взаимодействия с пользователем.
Ключевые слова: компьютерная обработка изображений, цифровая вычитающая рентгенография, объемная компьютерная томография, увеличение альвеолярного гребня
Введение
Во многих областях медицины (торакальная онкология, челюстно-лицевая хирургия, пародонтология и т. Д.) Оценка объемных различий между двумя модальностями с анатомической информацией (КТ, МРТ), полученной через различные промежутки времени. 1 Количественно оценивая эти различия, эксперты могут определить объемные изменения в характеристиках изображения, которые связаны исключительно с прогрессированием или регрессом определенного заболевания или патоморфологическим состоянием, и, таким образом, оценить эффективность определенной терапии или хирургической процедуры. 2,3
Самый простой и эффективный способ оценить различия между двумя наборами стоматологических данных, полученных в разные периоды времени, — это цифровая вычитающая рентгенография. 1-4 Исследования показали, что успех субтракционной рентгенографии зависит от уровня стандартизации геометрии проекции. 5 Однако стандартизация геометрии проекции во время съемки — это только первый шаг к успешной субтрактивной рентгенографии.Поскольку воспроизводимость геометрии изображения не может быть гарантирована, перед вычитанием часто требуется пространственная регистрация. 6,7 В литературе был предложен широкий спектр методов совмещения для совмещения двумерных (2D) медицинских изображений различных модальностей. 8,9 Хотя эти методы точны и эффективны при применении к 2D-изображениям, геометрия проекции, используемая при работе с наборами трехмерных (3D) изображений, требует другого подхода.Некоторые важные особенности, такие как расположение нижнечелюстного канала, верхнечелюстных пазух, носовой полости и угол альвеолярного гребня, не могут быть полностью представлены в двух измерениях и, следовательно, не могут быть учтены в процессе регистрации. 10 Кроме того, для клиницистов очень важно оценить трехмерные объемные изменения после реконструктивных процедур ( например, интеграция регенерированных или аугментированных тканей), а также наблюдать долгосрочную стабильность и поведение хирургически реконструированных твердых тканей. 11,12
По этой причине было предложено множество методов для регистрации наборов трехмерных данных. 13 В целом, большинство методов совмещения трехмерных изображений следуют принципам традиционной регистрации двухмерных изображений и работают с трехмерными реконструированными моделями, полученными из серии двумерных несовмещенных изображений. 14,15 Предполагается, что модель преобразования выравнивает указанный набор данных (плавающий набор) с эталонным набором данных посредством минимизации многомерной функции, Мера соответствия (MoM). 1 Методы регистрации 3D можно разделить на две широкие категории: основанные на характеристиках и основанные на интенсивности. Методы, основанные на признаках, основаны на идентификации и совмещении отличительных признаков между наборами объектов, таких как ориентиры, выступы или поверхности. 16-18 Функции могут быть обнаружены вручную (если требуется вмешательство пользователя) или с помощью специализированных алгоритмов автоматического обнаружения. В эту категорию попадают все техники, основанные на контурах и точках. Методы, основанные на признаках, обычно обеспечивают значительное преимущество в скорости по сравнению с подходами, основанными на интенсивности, но их эффективность прямо пропорциональна производительности алгоритма обнаружения признаков; поэтому ложные функции могут негативно повлиять на процесс регистрации.Однако методы регистрации, основанные на интенсивности, работают непосредственно с интенсивностями вокселей объектов трехмерных наборов данных. 19,20 Конкретные методы обычно намного медленнее, чем большинство подходов, основанных на функциях, но они обычно более точны, поскольку не нуждаются в обнаружении функций.
После успешного совмещения трехмерных объемных данных объекта их различия можно оценить с помощью стандартных методов цифровой рентгенографии с вычитанием. 1-4 Обычно эксперты выполняют линейные измерения на опорных и плавающих трехмерных объемах, чтобы оценить их различия в выбранных областях интереса, используя специализированные проприетарные пакеты программного обеспечения [ e.грамм. КТ челюстно-лицевого луча (КЛКТ) —iCAT Vision; 21 Imaging Sciences International, Хатфилд, Пенсильвания]. Причина этого в том, что не всегда можно вручную оценить объем различий из-за их геометрической формы или их положения. Однако линейные измерения могут обеспечить только приблизительную оценку объемных изменений между предметными наборами трехмерных данных в интересующей области (ROI). Во многих случаях это вполне приемлемо. Тем не менее, могут быть и другие случаи, когда требуется повышенная точность или когда различия не легко уловимы для человека-наблюдателя.В таких случаях необходима объемная оценка с помощью программного обеспечения. 22,23
В этой статье представлена полная методология регистрации наборов данных трехмерной дооперационной и послеоперационной КТ для оценки их объемных различий, соответствующих увеличению костной ткани в альвеолярной области для конкретных наборов. Таким образом, это исследование преследует двоякую цель; во-первых, чтобы описать методы и методы, используемые для автоматического выравнивания трехмерных данных, и, во-вторых, чтобы определить подходящую схему объемной оценки, чтобы количественно определить и оценить разницу между дооперационными и согласованными послеоперационными наборами данных.В этом исследовании использовалось 20 наборов, каждый из которых состоит из 2 томов (для дооперационных и послеоперационных данных). Два объема в каждом наборе были выровнены с использованием техники трехмерной регистрации. Затем выровненный послеоперационный объем сравнивали с дооперационным объемом. Сравнение проводилось с помощью цифровой рентгенографии с вычитанием, чтобы выявить различия между двумя вычтенными объемами. Разница в выбранных ROI учитывалась для оценки разнообразия дооперационных и послеоперационных данных в конкретных регионах.В большинстве случаев предлагаемый метод регистрации позволял успешно выровнять трехмерные объемы, тем самым улучшая результаты объемной оценки.
Материалы и методы
Предлагаемая схема оценки объема включает два отдельных этапа: регистрацию предметных трехмерных данных и оценку их объемных различий в выбранной области инвестиций. Полная методология проиллюстрирована в. В этом разделе описаны методы, используемые для регистрации дооперационных и послеоперационных данных в каждом наборе, а также методы, используемые для объемной оценки различий между зарегистрированными наборами.
Принципиальная блок-схема полной предложенной схемы для оценки объемных различий между двумя томами
Сбор данных
20 пациентов, которым требовалась имплантотерапия и имели альвеолярные дефекты, лечили с использованием двухэтапного хирургического доступа. Первый этап включал процедуру увеличения с использованием конструкции лоскута частичной толщины. По возможности одновременно устанавливались имплантаты (Branemark / Replace; Nobel Biocare, Гетеборг, Швеция). Беззубый гребень был увеличен по вертикали и горизонтали с помощью нерезорбируемого бычьего минерала (Bio-Oss; Geistlich, Wolhusen, Швейцария) и местных костных стружек.После трансплантации нерезорбируемая титановая мембрана (FRIOS® Bone Shield; Dentsply Friadent, Мангейм, Германия) или рассасывающаяся мембрана (Resolut Adapt LT; Gore, Flagstaff, AZ) была обрезана и адаптирована к области трансплантации. Мембрана фиксировалась титановыми штифтами (FRIOS® Membrane Tacks; Dentsply Friadent). Повторный вход был произведен через 9–12 месяцев после операции. Клинически увеличенный по вертикали и горизонтали альвеолярный гребень имел клинический вид, похожий на соседнюю кость. Ранее открытые поверхности имплантата были покрыты вновь сформированной твердой тканью.Фиксирующие винты и винты-заглушки были удалены, чтобы обеспечить доступ для соединения абатмента. Наконец, были установлены заживляющие абатменты. Было получено 20 наборов данных из примененного хирургического протокола для увеличения альвеолярного гребня, описанного выше, по одному для каждого пациента. Хирургические процедуры были выполнены, и полученные наборы были предоставлены PW на кафедре пародонтологии Университета Земмельвейса, Будапешт, Венгрия.
Наборы данных, представленные в этом исследовании, были получены после одобрения, предоставленного Региональным и институциональным комитетом по науке и этике исследований Университета Земмельвейса (номер ссылки: 77/2011).Каждый набор состоит из двух томов изображений КЛКТ для дооперационного и послеоперационного представления каждого пациента. Комбинированные срезы КТ в каждом случае представляют собой полное трехмерное изображение пациентов с акцентом на альвеолярные изменения до и через 9–12 месяцев после операции. Все снимки КЛКТ были получены с помощью оборудования источника рентгеновского излучения Classic i-CAT® (Imaging Sciences International). Наборы данных были получены при комплексном аугментативном и протезном лечении пациентов с использованием имплантатов.Принимая во внимание, что дозировка сканирования i-CAT не значительно выше по сравнению с меньшим объемом CBCT, система i-CAT была предпочтительнее, поскольку во всех случаях необходимо было оценить дополнительные хирургические участки и эндодонтическое лечение.
Все наборы данных были получены с использованием общего набора параметров для сканера i-CAT: высокая частота, постоянный потенциал, фиксированный анод 120 кВп, 3–8 мА (импульсный режим). Детектор изображения представлял собой плоскую панель из аморфного кремния размером 20 × 25 см.Получение изображения осуществлялось в сидячем положении путем одного вращения на 360 ° со стандартным временем сканирования 40 с.
Все доступные наборы данных были отформатированы в стандарте цифровой визуализации и коммуникации в медицине (DICOM) как серии 16-битных изображений в градациях серого (соответствующих отдельным срезам КТ). Размер всех изображений составлял 400 × 400 пикселей с размером пикселя 0,4 × 0,4 мм. Расстояние между срезами оставалось постоянным для всех наборов и составляло 0,4 мм. Количество срезов (изображений) в каждом наборе составляло 322–327, в зависимости от пациента.Чтобы упростить обработку данных, все наборы DICOM были преобразованы в 8-битные наборы данных RAW в оттенках серого с помощью утилиты XMedCon с открытым исходным кодом. 24
Методика 3D-регистрации
Предлагаемая методика объемной оценки основана на прямом сравнении дооперационных и послеоперационных 3D-объемов. Сравнение выполняется с точки зрения разницы между двумя томами на послойной основе. Однако этот процесс требует, чтобы два сравниваемых набора были правильно выровнены.Поскольку это исследование касается объемных данных, необходимо использовать подходящую схему трехмерной регистрации, чтобы выровнять рассматриваемые объемы. В нашем случае послеоперационный объем записывается в дооперационный объем. Следовательно, дооперационный объем рассматривается как эталонный набор данных, а послеоперационный объем рассматривается как плавающий набор на протяжении всего исследования.
Объемные наборы данных этого исследования могут быть представлены в виде серии плоских изображений, каждое из которых обозначает объемный срез.Как и любой метод регистрации, предлагаемый метод состоит из трех основных компонентов:
Функция преобразования для соответствующего преобразования координат точек плавающего объема.
MoM (или целевая функция) для вычисления ошибки между контрольным объемом и оцененным преобразованным объемом.
Метод оптимизации, который будет использовать MoM для оценки оптимальных параметров модели преобразования. Оптимальные параметры должны обеспечивать наилучшее выравнивание плавающего объема с эталонным объемом.
Аффинная модель
Функция преобразования, предпочтительная в предлагаемой схеме трехмерной регистрации, представляет собой аффинное преобразование, способное преобразовывать точки в трехмерном пространстве. Трехмерная аффинная модель, используемая в этом исследовании, показана в уравнении 1:
(1)
, где 12 независимых параметров аффинной модели соответствуют i = 1,2,3 и dx, dy и dz. . Следовательно, точки из плавающего объема с начальными координатами могут быть преобразованы в их новые координаты, учитывая следующие равенства:
(2)
Применяя функцию преобразования, описанную в уравнении 2, в каждой точке плавающего трехмерного объема, весь Объем может быть преобразован в пространстве в соответствии с вращением, масштабированием и перемещением, определяемым 12 параметрами модели преобразования.Поскольку все параметры являются действительными числами, вычисленные преобразованные координаты также являются действительными числами. По этой причине в предлагаемой схеме используется метод трилинейной интерполяции, при котором восемь соседних точек рассматриваются для оценки интенсивности каждой преобразованной точки. 25
Целевая функция абсолютной разности
В общем, регистрация изображений — это рекурсивный процесс проб и ошибок. На каждой итерации вновь преобразованная оценка сравнивается с эталонным изображением или набором данных.Оценка выполняется с помощью целевой функции или MoM. В большинстве схем регистрации изображений используются хорошо известные целевые функции, такие как коэффициент корреляции, взаимная информация, карта расстояний и так далее. 26,27 Эти функции очень эффективны для двумерной регистрации, но включают относительно большое количество арифметических вычислений, что делает их непрактичными для больших объемов данных. К сожалению, размер наборов данных, используемых в нашем исследовании (более 320 CT-срезов каждый), позволяет использовать только довольно простые целевые функции.
Таким образом, целевая функция, предпочитаемая в этом исследовании, представляет собой среднюю абсолютную разницу между контрольным и согласованным объемом для каждой точки. Математически это может быть выражено, как показано в Уравнении 3:
(3)
, где — интенсивность (уровень серого) точки из эталонного объема и — интенсивность точки из плавающего объема. Фактически, уравнение 3 вычисляет среднюю абсолютную разницу между эталонным и преобразованным плавающим объемом по всем срезам ( N ) с точками ширины ( W, ) и высоты ( H ).Отсюда следует, что чем ниже измеренная средняя абсолютная разность, тем лучше совпадают эталонный и преобразованный плавающие объемы.
Метод симплексной оптимизации
Функция преобразования и MoM, описанные в предыдущих разделах, должны быть правильно скомбинированы, чтобы добиться выравнивания двух предметных томов. Следовательно, на каждой итерации схемы регистрации функция преобразования должна быть снабжена новым набором параметров, которые в идеале должны минимизировать целевую функцию.В большинстве схем регистрации это обычно достигается с помощью метода оптимизации. Процесс оптимизации оценивает новые параметры преобразования в попытке сблизить два объема в пространстве после каждой итерации. В нашем случае это достигается минимизацией средней абсолютной разности MoM, описанной в уравнении 3.
Предлагаемая схема трехмерной регистрации использует симплексный метод спуска для оптимизации параметров преобразования. 28 Конкретный метод представляет собой повторяющуюся процедуру, которая прокладывает свой собственный путь вниз через топографию с размерами M , пока не встретит хотя бы локальный минимум (или максимум).Симплексный метод спуска должен быть инициализирован позициями, определяющими начальный симплекс. Если одна из этих позиций является начальной отправной точкой, тогда другие позиции M могут быть выражены как P i = P 0 + e i , где значения e i — это M единичных векторов. Затем алгоритм выполняет ряд шагов, заменяя позиции, в которых целевая функция максимизируется (наихудшее решение), новой позицией.Новое положение определяется путем экстраполяции поведения целевой функции, измеренной в каждой позиции, которая организована как симплекс. В нашем случае были определены два критерия завершения: симплекс был перемещен меньше заданного допуска в конкретной итерации (было достигнуто незначительное улучшение) или было достигнуто максимальное количество итераций.
Оценка регистрации
Эффективность процесса выравнивания можно оценить путем оценки среднего краевого расстояния между дооперационным объемом и выровненным послеоперационным объемом.Алгоритм, используемый в нашем случае, состоит из следующих шагов:
извлечение краев всех срезов из эталонного набора (до операции) с помощью детектора края canny 29
извлечение краев всех срезов из выровненного плавающего набора (после операции) с использованием того же метода
Расчет критерия среднего краевого расстояния (MED) для оценки кратчайшего расстояния между каждой краевой точкой опорного и выровненного плавающих объемов на срезе -резцевая основа.
Критерий MED между контрольным объемом и выровненным плавающим объемом рассчитывается следующим образом:
(4)
где — количество краевых точек в срезе z выровненного плавающего объема, являются координатами граничная 2D точка из среза z выровненного плавающего объема и является картой расстояний среза z от выровненного плавающего объема. 30 Фактически, уравнение 4 описывает двухэтапный процесс:
вычисление среднего расстояния по карте расстояний каждой пары срезов
вычисление среднего расстояния по всем срезам.
Значение MED измеряется в точках (пикселях), но если размеры в метрических пикселях полученных наборов данных известны заранее, измерения можно преобразовать в любую метрическую единицу (миллиметры, сантиметры и т. Д.). Оценочные результаты представлены в следующих разделах.
Объемная оценка
Схема регистрации, описанная ранее, была использована для обеспечения эффективной объемной оценки объемов компьютерной томографии после операции. Это должно быть достигнуто путем прямого сравнения согласованных дооперационных и послеоперационных данных и оценки их различий.Для этого была разработана схема объемной оценки, основанная на цифровой субтракционной рентгенографии.
Основная идея предлагаемого метода объемной оценки заключается в том, что разница в объеме между дооперационными и послеоперационными наборами данных в конкретной интересующей области должна быть выявлена после цифрового вычитания выровненных версий двух наборов. Следовательно, нет необходимости получать измерения объема из обоих наборов данных, так как разность объемов может быть рассчитана путем простого изучения результата вычитания.Предлагаемый алгоритм включает в себя следующие процессы последовательно:
цифровое вычитание дооперационного и выровненного послеоперационного объемов на послойной основе
определение ROI в каждом срезе вычитание результирующего объема (разностный объем)
объемных измерений путем объединения определенных областей интереса.
Цифровое вычитание
При условии, что два набора предметных данных правильно выровнены, цифровое вычитание между этими двумя наборами должно выявить их различия.В частности, в случае трехмерных данных эти различия могут быть смоделированы как объекты в трехмерном пространстве. Это идеально подходит для нашего случая, когда нам нужно оценить изменения в трехмерных послеоперационных данных по сравнению с дооперационными данными для того же пациента.
Типичная цифровая рентгенография вычитания обычно выполняется путем получения абсолютной разницы между сравниваемыми изображениями или наборами данных. В нашем случае этот принцип расширен до трех измерений, причем третьим измерением является глубина среза.Таким образом, создается новый том (), который соответствует абсолютной разнице между дооперационным и послеоперационным объемами на послойной основе. Это может быть выражено математически, как показано в уравнении 5 для объемов N срезов с шириной ( W ) и высотой ( H ):
(5)
Практически, интенсивность каждой точки в 3D пространство — это абсолютная разница между интенсивностью соответствующей точки дооперационного объема () и выровненным послеоперационным объемом ().При условии, что два сравниваемых объема были успешно выровнены, должен быть объем низкой интенсивности (темный), позволяющий различать различия между двумя предметными объемами. В этом исследовании эти различия соответствуют вновь сформированным твердым тканям, возникшим в результате хирургической процедуры, описанной ранее.
Определение областей интереса
После извлечения разностного объема можно определить интересующую область. Конкретная область — это часть трехмерного объема, которая содержит изменения, которые необходимо оценить.Как уже упоминалось, все наборы данных, используемые в этом исследовании, состоят из серии 2D-изображений, соответствующих объемным срезам. Следовательно, определяя ROI в каждом слайсе, интересующий объем (VOI) может быть составлен после объединения всех последовательных областей. Определение ROI можно описать как проблему сегментации изображения. В результате можно использовать любой типичный метод 2D-сегментации, если он применяется ко всем объемным срезам.
Для целей данного исследования предпочтение было отдано схеме, основанной на методе сегментации по возрастанию области. 31 Предлагаемая схема состоит из следующих последовательных шагов, которые применяются к продукту вычитания (разностному объему) дооперационного и послеоперационного объемов:
Предлагаемый алгоритм представляет собой полуавтоматический процесс, требующий только определения области поиска. Однако могут быть некоторые фрагменты, в которых алгоритм увеличения области не может обнаружить область. Это может быть связано либо с неправильной начальной начальной точкой, либо с неподходящим порогом. В таких случаях необходима ручная регулировка.
В данном исследовании использовалась дополнительная техника сегментации в качестве альтернативы выращиванию регионов. Этот метод основан на выделении пороговых зон интенсивности в каждом срезе предметного объема. Альтернативный метод сегментации, который также применяется к продукту вычитания дооперационного и послеоперационного объемов, можно резюмировать следующим образом:
Ручное определение широкой прямоугольной области поиска или нескольких многоугольных областей поиска в каждом срезе
Определение фиксированного количества пороговых зон интенсивности (путем определения верхней и нижней границ каждой зоны)
Обработка первого среза:
Классифицируйте точки области (ей) поиска по одной из предопределенные зоны интенсивности в соответствии с их интенсивностью
Вручную выберите одну или несколько зон в качестве области интереса среза
Повторите для всех срезов.
Процедура, описанная выше, требует большего вмешательства пользователя, чем относительно автоматизированный метод наращивания области, проиллюстрированный ранее, но в целом обеспечивает более точную сегментацию, чем рост области.
Объемные измерения
Заключительным этапом алгоритма объемной оценки является получение метрических измерений VOI. Зная метрические размеры точек (разрешение) и расстояние между срезами наборов данных, VOI может быть выражен в метрических единицах, используя уравнение 6:
(6)
В уравнении 6 измерения получают по всем Нм. кусочка объема продукта вычитания.Величины X res , Y res и Z res соответствуют разрешению x , y -разрешению и межсрезовому расстоянию, соответственно, которые для всех равны 0,4. наборы в этом исследовании. Другими словами, уравнение 6 определяет сумму всех точек ROI с объемом в каждом слайсе z и для всех N слайсов.
Верификация объемных измерений
Полученные объемные измерения были проверены путем оценки объемов пяти объектов стандартной формы с известными размерами.Объекты были измерены вручную, и их реальные объемы были рассчитаны математически. Затем предложенный алгоритм оценки объема был применен к тем же объектам, и два полученных измерения были сопоставлены.
Первым эталонным объектом, использованным в данном исследовании, является дентальный имплант. Конкретный имплантат можно приблизительно представить как объект в форме полуконуса с высотой h = 8,5 мм, диаметром верхней поверхности D , верхней = 3,57 мм и диаметром нижней поверхности D bot = 2.761 мм. Согласно математическим свойствам полуконуса, его объем можно рассчитать с помощью уравнения 7:
(7)
Остальные эталонные объекты представляли собой четыре цилиндрических имплантата различных размеров. Объем цилиндра с диаметром и высотой может быть математически рассчитан с помощью уравнения 8:
(8)
Результаты
В этом разделе представлены результаты, полученные путем применения предложенного метода ко всем наборам данных, представленных в этом исследовании. В частности, исследуются два аспекта алгоритма: регистрация (выравнивание) и оценка объема.
Оценка регистрации
Эффективность предложенной схемы регистрации была оценена как качественно, так и количественно. Результаты представлены в следующих разделах.
Качественная оценка
Качественная оценка проводилась посредством визуальной оценки. Чтобы достичь этого, дооперационный, послеоперационный и выровненный послеоперационный наборы были реконструированы с использованием стороннего инструмента трехмерного просмотра объема (программа просмотра объема ImageJ; см. Vog.hin.nodoc@enyaw). 32 Предоперационный и послеоперационный тома были затем объединены вместе до и после процесса регистрации, чтобы визуально продемонстрировать эффекты регистрации. показывает эти реконструированные объемы для трех наборов (наборы I, II и III). В предоперационном объеме изображен с наложенным послеоперационным объемом, видимым в виде заштрихованных областей. Как видно на фиг., Наблюдается заметное улучшение во всех случаях (), поскольку в трех исследованных случаях было достигнуто удовлетворительное выравнивание между дооперационным и послеоперационным объемами (наборы I – III).С другой стороны, в незарегистрированных наборах () плавающий объем демонстрирует довольно большое пространственное отклонение по сравнению с эталонным объемом, особенно для наборов II и III (соответственно).
Объединенные предоперационные и послеоперационные объемы до и после регистрации для визуализации эффектов процесса регистрации на трехмерные реконструированные версии (a) набора I до регистрации, (b) набора I после регистрации, (c ) Набор II до регистрации, (d) Набор II после регистрации, (e) Набор III до регистрации и (f) Набор III после регистрации
Количественная оценка
Предложенная схема 3D-регистрации также была количественно оценена с использованием MED между два тома.В нашем случае уравнение 4 использовалось для получения измерений MED между дооперационным и послеоперационным объемами до и после процесса регистрации. Значения MED до и после регистрации можно рассматривать как количественную оценку улучшения, достигнутого с использованием предложенной схемы трехмерной регистрации, в том, что касается выравнивания двух объемов. Измерения MED были получены для всех 20 пациентов до и после применения алгоритма регистрации.Для удобства измерения, полученные из уравнения 4, были преобразованы в миллиметры, и результаты для всех наборов проиллюстрированы на.
Таблица 1
Расчетное среднее расстояние от края до края (MED) в миллиметрах для всех наборов (при размере пикселя 0,4 × 0,4 мм)
| Набор | До регистрации | После регистрации | |||
| I | 4,090 | 0,988 | |||
| II | 5.072 | 0,758 | |||
| III | 12,996 | 1,143 | |||
| IV | 3,582 | 1,274 | |||
| V | 13.203 | 4 9042 9042 9042 904 304 9042 9042 9042 904 304 9042 904 304||||
| VII | 7,295 | 0,883 | |||
| VIII | 15,958 | 1,607 | |||
| IX | 34,452 | 5.787 | |||
| X | 15,881 | 5,824 | |||
| XI | 3,756 | 0,242 | |||
| XII | 11,754 | 1,6354 904 | 9 11,7541,614 904 904 | 13,323 | 0,102 |
| XV | 23,298 | 0,447 | |||
| XVI | 18,459 | 0,878 | |||
| XVII 904.000 | 0,265 | ||||
| XVIII | 14,910 | 1,037 | |||
| XIX | 7,508 | 1,182 | |||
| XX | |||||
| XX | 10,6994 9035 9042 9042 9 10,6994 | 1,483 ± 1,558 |
Как видно из, достигаемое улучшение напрямую зависит от характеристик каждого набора. В общем, небольшие значения MED соответствуют близкому пространственному совпадению между двумя объемами и, следовательно, лучшему выравниванию.В 18 случаях из 20 предложенная схема регистрации достигла значений МЭД менее 2 мм. Более того, в девяти случаях были зафиксированы значения МЭД менее 1 мм. Эти значения соответствуют почти идеальному совпадению между дооперационным и послеоперационным объемами в ROI. Полученные относительно высокие результаты измерений, особенно для наборов IX и X in, приписываются различным металлическим артефактам на конкретных наборах, которые создают неравномерно распределенные отражения. Эти отражения учитываются алгоритмом детектора кромок, в результате чего среднее значение расстояния до кромки немного увеличивается.Тем не менее, затронутые наборы все еще можно использовать, как обсуждается позже, при выполнении объемных измерений.
Объемная оценка
Как и регистрационная оценка, объемная оценка также была выполнена посредством визуального осмотра и количественных измерений. Результаты, полученные для всех наборов, проиллюстрированы в следующих разделах.
Качественная оценка
ROI были извлечены в каждом наборе из разностных объемов с использованием предложенной методологии.Визуальная оценка проводилась в каждом срезе разностного объема, чтобы проверить достоверность извлеченной области интереса. Некоторые примеры показаны на, где изображены определенные области интереса на выбранных срезах разностного объема из наборов I – III (области в кружках). Комбинируя обнаруженный ROI из всех срезов, мы можем получить VOI для каждого набора. В, обнаруженные VOI обозначены для наборов I – III (области, обведенные кружком). VOI проиллюстрированы на трехмерных реконструированных версиях слияния между дооперационным набором и разностным объемом.
Интересующие области (ROI) и объемы интереса (VOI) для всех наборов. Рентабельность инвестиций для (а) набора I, (б) набора II и (в) набора III. VOI на трехмерных реконструированных версиях (d) набора I, (e) набора II и (f) набора III
Количественная оценка
Количественные измерения были получены для каждого VOI с использованием уравнения 6. Объем каждого VOI был выражен в метрическая система единиц как кубические миллиметры. Результаты, касающиеся VOI, как показано в наборах I – III, соответственно, представлены для всех 20 наборов, представленных в этом исследовании.
Таблица 2
Объемные измерения для всех 20 комплектов
| Набор | Объем (мм 3 ) | |
| I | 1076 | |
| III | 1962 | |
| IV | 1040 | |
| V | 431 | |
| VI | 431 | |
| VII | 4||
| 512 | ||
| X | 330 | |
| XI | 964 | |
| XII | 1154 | |
| XIII | 1512 | 9 XIII1512 | 216
| XVI | 636 | |
| XVII | 628 | 9 0435|
| XVIII | 480 | |
| XIX | 407 | |
| XX | 785 |
Как уже упоминалось, объемные измерения были проверены путем сравнения реального объема пяти эталонных объектов с реальным объемом Применение предложенной схемы.Используя уравнение 7 и уравнение 8 и подставляя значения, измеренные для наших эталонных объектов, были вычислены их реальные объемы. Затем ко всем эталонным объектам был применен метод оценки объема, описанный в уравнении 6, с получением их оценочных объемов в метрических единицах. Реальные и предполагаемые измерения для каждого эталонного объекта показаны на. Как видно на, эти два измерения во всех случаях практически совпадают, поскольку их зарегистрированные различия составляют менее 0,4 мм 3 . Пример первого эталонного объекта в форме полуконуса показан в (обведенная область) в трехмерном представлении набора V.иллюстрирует увеличенный фрагмент изображения с фокусом на интересующей области.
Эталонный объект (имплант) в форме полуконуса, используемый для проверки предложенной схемы оценки объема, проиллюстрированный в трехмерной реконструированной версии набора V. (a) Полный объем, исходный размер и (b) увеличенный разрез имплантата
Таблица 3
Объемные измерения пяти эталонных объектов для проверки алгоритма оценки объема
| Имплант (форма) | Размеры (мм) | Set | Реальный объем (мм 3 ) | Расчетный объем (мм 3 ) | |||||||
| Имплантат 1 (полуконус) | h = 8.5 D верх = 3,75 D бот = 2,761 | V | 71,289 | 71,360 | |||||||
| Имплант 2 (цилиндрический) | IX h = 10 904 D = 3,92 | 110.491 | 110.528 | ||||||||
| X | 110.464 | ||||||||||
| XVII | 110.656 | ||||||||||
| XVIII | 110.848 | IX | 144,571 | 144,576 | |||||||
| Имплант 4 (цилиндрический) | h = 8,5 D = 4 | IX | 106,857 | IX | 106,857 | 106 5 (цилиндрический) | h = 8,5 D = 3,75 | XVIII | 93,917 | 93,888 |
Обсуждение
Для клиницистов очень важно получить линейные измерения, описывающие максимальную протяженность увеличенные твердые ткани в вертикальном и горизонтальном размерах.Эти линейные измерения предоставляют информацию об успехе и ограничениях определенной хирургической техники. Хотя конкретные линейные измерения достаточно точны, они могут дать только оценку объема увеличенной кости. В подавляющем большинстве случаев рассчитать конкретный объем невозможно из-за нестандартной геометрической формы VOI. Кроме того, традиционный подход требует получения двух наборов измерений (на основе дооперационных и послеоперационных данных) и нескольких образцов на одно измерение, что является довольно утомительным и трудоемким процессом.Более того, для клиницистов очень важно обеспечить трехмерные объемные измерения вновь сформированных твердых тканей без выполнения предполагаемых множественных линейных измерений на двух разных, несовмещенных наборах данных. Предлагаемая методология позволяет оценить успех поэтапных и одновременных процедур увеличения твердых тканей, а также предоставить новый подход для сравнения эффективности различных хирургических подходов. Таким образом, можно разработать стандартизированную методологию для сравнения результатов объемного измерения различных аугментативных техник.Предлагаемая схема позволяет получить одно воспроизводимое измерение объема на основе разницы выровненных дооперационных и послеоперационных объемов при минимальном взаимодействии с пользователем. Применяя предложенную схему для оценки объема наряду с линейными измерениями, можно даже сравнить эффективность различных хирургических методов, приводящих к изменениям твердых тканей.
Предлагаемая схема зависит от цифровой рентгенографии с вычитанием, чтобы выявить различия между двумя предметными наборами трехмерных данных.Как и в случае любого другого метода цифровой рентгенографии с вычитанием, успешное совмещение двух наборов является строгим требованием. Фактически, эффективность всей схемы прямо пропорциональна качеству 3D-регистрации. Как упоминалось ранее, схема регистрации, используемая в этом исследовании, использует аффинную модель в качестве функции преобразования, абсолютную разницу в качестве целевой функции и метод симплексного спуска в качестве метода оптимизации.
В целом модели трансформации можно разделить на две большие категории: жесткие и нежесткие.Нежесткие модели обычно определяются упругими преобразованиями, которые могут свободно искажать преобразованный объект. С другой стороны, жесткие методы обеспечивают несколько более управляемую модель преобразования, которая искажает преобразованный объект относительно конечного числа плоскостей. Следовательно, в случае 3D-данных объект может быть преобразован относительно вертикальной и горизонтальной плоскостей. Поскольку 20 наборов трехмерных данных, использованных в этом исследовании, не содержали каких-либо серьезных упругих деформаций, в предложенную схему трехмерной регистрации была включена жесткая модель.Фактически, наиболее обобщенная жесткая модель, аффинное преобразование, предпочтительнее для объяснения широкого круга случаев.
Как уже упоминалось, огромный размер наборов данных, представленных в этом исследовании, требует довольно простой и быстрой целевой функции для выравнивания трехмерных объемов в течение разумного периода времени. Как правило, традиционные схемы двумерной регистрации используют довольно сложные метрики MoM, такие как коэффициент корреляции, корреляция градиента, взаимная информация, карта расстояний и так далее.Хотя эти показатели обеспечивают повышенную точность, они применимы только для оценки отдельных изображений или небольших последовательностей изображений. Некоторые из этих показателей были протестированы в качестве целевой функции в предложенной схеме с использованием некоторых наборов трехмерных данных, представленных в этом исследовании. Качество регистрации было удовлетворительным во всех случаях, но увеличившееся время, необходимое для настройки наборов, сделало эту схему непрактичной. Например, потребовалось около 5 часов для регистрации набора 3D данных из 325 срезов с использованием коэффициента корреляции и около 7 часов для того же набора с использованием взаимной информации в качестве MoM.С другой стороны, используемая схема абсолютных разностей, описанная в уравнении 3, требовала около 2 часов для того же набора. Время выполнения остальных данных было прямо пропорционально размеру наборов 3D-данных. В целом, все представленные наборы содержали 322–327 срезов, поэтому время выполнения немного отклонялось — около 2 часов. Все тесты проводились на одной и той же эталонной системе [процессор AMD Mobile Sempron (Саннивейл, Калифорния) с частотой 1,6 ГГц, 2 ГБ ОЗУ, операционная система Microsoft Windows XP (Редмонд, Вашингтон)].
Ограничения по времени выполнения также наложили использование только симплексного метода спуска в качестве метода оптимизации для предлагаемого алгоритма трехмерной регистрации. В большинстве случаев двумерной регистрации симплексный метод обычно сочетается с другими методами оптимизации (такими как метод Пауэлла) для повышения точности. Однако такой подход будет непрактичным для трехмерных наборов из более чем 320 срезов, представленных в этом исследовании. Производительность алгоритма регистрации можно было бы улучшить, если бы вместо этого использовались версии наборов с пониженной выборкой.В таком случае выравнивание будет намного быстрее. Однако это также может отрицательно повлиять на точность всей схемы, поскольку объемные измерения должны быть получены на объемах с пониженной дискретизацией и меньшим разрешением.
Области интереса были определены на разностных объемах с использованием одного из двух предложенных полуавтоматических методов сегментации: увеличение области или зоны интенсивности на основе пороговых значений. Было проведено несколько испытаний с использованием обоих методов на одних и тех же наборах данных, а извлеченные ROI были изучены экспертами.Был сделан вывод, что зоны интенсивности на основе пороговых значений предоставляют экспертам более контролируемый метод определения ROI и, следовательно, считаются более точными, чем рост области. В результате именно этот подход был предпочтен в большинстве наборов, представленных в этом исследовании.
Все вышеперечисленные замечания говорят о том, что предлагаемая комбинационная схема регистрации и оценки разности объемов является достаточно гибкой. Модульная конструкция самой схемы предоставляет несколько возможностей для улучшений, оптимизаций и настроек в соответствии с исследованными данными.Отсюда следует, что алгоритм, используемый для целей этого исследования, был специально адаптирован для больших наборов стоматологических данных 3D изображений компьютерной томографии, представленных в исследовании.
Заключение
В этом документе представлен метод автоматического выравнивания наборов стоматологических данных 3D КЛКТ. Предложенный метод был включен в полную схему количественной оценки и оценки объемных различий между двумя наборами данных. Тесты, проведенные в общей сложности на 20 наборах, показали, что предложенный метод успешно согласовал дооперационный и послеоперационный объемы в каждом наборе.Это позволило эффективно оценить объемные различия между дооперационными и выровненными послеоперационными объемами, используя предложенную методику оценки, основанную на цифровой вычитающей рентгенографии. Представленный новый рентгенологический подход представляет собой качественный и сравнительный метод оценки изменений твердых тканей после определенных вмешательств ( например, процедуры увеличения кости, эндодонтическое лечение). Предлагаемая схема также позволяет отслеживать прогрессирование или регресс определенных патологических состояний в челюстно-лицевой области ( e.грамм. хронические периапикальные воспалительные процессы, опухоли, инфильтрирующие твердые ткани).
Ссылки
1. Захараки Э.И., Мацопулос Г.К., Асвестас П.А., Грёндаль К., Грёндаль Х.Г. Схема цифровой рентгенографии с вычитанием, основанная на автоматической регистрации с множественным разрешением. Дентомаксиллофак Радиол 2004; 33: 1–14 [PubMed] [Google Scholar] 2. Webber RL, Ruttimann UE, Gröndahl HG. Вычитание рентгеновских снимков как основа для оценки изменений пародонта. J Periodont Res 1982; 17: 509–511 [PubMed] [Google Scholar] 3.Грёндаль Х.Г., Грёндаль К. Субтракционная рентгенография для диагностики поражения костей пародонта. Oral Surg Oral Med Oral Pathol 1983; 55: 208–513 [PubMed] [Google Scholar] 4. Редди М.С., Джеффкот МК. Цифровая субтракционная рентгенография. Dent Clin of North Am 1993; 37: 553–556 [PubMed] [Google Scholar] 5. Мол А, Данн С.М. Проведение проективной стандартизации для цифровой субтракционной рентгенографии. Oral Surg Oral Med Oral Pathol Oral Radiol Endod 2003; 96: 373–382 [PubMed] [Google Scholar] 6. Lehmann TM, Gröndahl HG, Benn DK.Компьютерная регистрация для цифрового вычитания в стоматологической радиологии. Дентомаксиллофак Радиол 2000; 29: 323–346 [PubMed] [Google Scholar] 7. Юн, округ Колумбия. Новый метод автоматического совмещения стоматологических рентгенограмм для цифровой субтракционной рентгенографии. Дентомаксиллофак Радиол 2000; 29: 11–19 [PubMed] [Google Scholar] 8. Мацопулос Г.К., Асвестас П.А., Муравлянский Н.А., Делибасис К.К. Мультимодальная регистрация изображений сетчатки глаза с помощью самоорганизующихся карт. IEEE Trans Med Imag 2004; 23: 1557–1563 [PubMed] [Google Scholar] 9.Lehmann TM, Gröndahl K, Gröndahl HG, Schmitt W, Spitzer K. Независимая от наблюдателя регистрация перспективной проекции перед вычитанием рентгенограмм in vivo. Дентомаксиллофак Радиол 1998; 27: 140–150 [PubMed] [Google Scholar] 10. Lofthag-Hansen S, Gröndahl K, Ekestubbe A. КТ с коническим лучом для предоперационного планирования установки имплантата в задней части нижней челюсти: видимость анатомических ориентиров. Clin Implant Dent Relat Res 2009; 11: 246–255 [PubMed] [Google Scholar] 11. Симион М, Йованович С.А., Тинти С., Бенфенати С.П.Долгосрочная оценка остеоинтегрированных имплантатов, установленных во время или после увеличения вертикального гребня. Ретроспективное исследование 123 имплантатов с периодом наблюдения 1–5 лет. Clin Oral Implants Res 2001; 12: 35–45 [PubMed] [Google Scholar] 12. Далин С., Симион М., Хатано Н. Долгосрочное наблюдение на уровне мягких и твердых тканей после лечения направленной регенерации кости в сочетании с ксеногенным пломбировочным материалом: 5-летнее проспективное клиническое исследование. Clin Implant Dent Relat Res 2010; 12: 263–270 [PubMed] [Google Scholar] 13.Maintz JBA, Viergever MA. Обзор регистрации медицинских изображений. Мед им анальный 1998; 2: 1–36 [PubMed] [Google Scholar] 14. Lofthag-Hansen S, Huumonen S, Gröndahl K, Gröndahl HG. КТ с ограниченным пучком и внутриротовая рентгенография для диагностики периапикальной патологии. Эндод Med Oral Pathol Oral Radiol 2007; 103: 114–119 [PubMed] [Google Scholar] 15. Шамплбу Дж., Лавалле С., Селиски Р., Брюни Л. От точной калибровки датчика изображения дальности до точной локализации 3D-объекта на основе модели. Материалы CVPR: Конференция компьютерного общества по компьютерному зрению и распознаванию образов.IEEE Computer Society 1986: 435–437 [Google Scholar] 16. Харткенс Т., Рор К., Штиль Х.С. Оценка 3D-операторов для обнаружения анатомических точечных ориентиров на МР- и КТ-изображениях. Comp Vis Im Under 2002; 86: 118–136. [Google Scholar] 17. Бесл П.Дж., Маккей Н.Д. Метод регистрации трехмерных фигур. IEEE Trans Patt Anal Mach Intell 1992; 14: 239–256 [Google Scholar] 18. Мацопулос Г.К., Муравлянский Н.А., Асвестас П.А., Делибасис К.К., Кулулиас В. Грудная нежесткая регистрация, сочетающая самоорганизующиеся карты и радиальные базисные функции.Мед им анальный 2005; 9: 237–254 [PubMed] [Google Scholar] 19. Паррага А., Крейн, доктор медицины, Петтерссон Дж., Сусин А., Макк Б. Оценка нежестких методов регистрации 3D КТ изображений для лучевой терапии головы и шеи. Proc. Медицинская визуализация SPIE. Сан-Диего, Калифорния; 2007 [Google Scholar] 20. Золлей Л., Гримсон Э., Норбаш А., Уэллс В. 2D – 3D жесткая регистрация рентгеновских рентгеноскопических и компьютерных изображений с использованием взаимной информации и оценок гистограмм с редкой выборкой. Comp Vis Patt Rec 2001; 2: 696–703 [Google Scholar] 22. Гавриелидес М.А., Киннард Л.М., Майерс К.Дж., Петрик Н.Некальцинированные узелки в легких: объемная оценка с помощью КТ грудной клетки. Радиология 2009; 251: 26–37 [Бесплатная статья PMC] [PubMed] [Google Scholar] 23. Калкнер К., Кубичек Дж., Нильссон Дж., Лунделл М., Левитт С., Нильссон С. Определение объема простаты: дифференциальные измерения объема, сравнивающие КТ и ТРУЗИ. Лучевая терапия Онкол 2006; 81: 179–183 [PubMed] [Google Scholar] 24. Нольф Э. XMedCon — набор инструментов для преобразования медицинских изображений с открытым исходным кодом. Евро J Nucl Med 2003; 30: S246 [Google Scholar] 25. Мейеринг Э. Хронология интерполяции: от древней астрономии до современной обработки сигналов и изображений.IEEE Proc 2002; 90: 319–342 [Google Scholar] 26. Лалиберте Ф., Ганьон Л, Шэн Ю. Регистрация и объединение изображений сетчатки: оценочное исследование. IEEE Trans Med Imaging 2003May; 22 (5): 661–73 [PubMed] [Google Scholar] 27. Эдвардс АЛ. Коэффициент корреляции. Введение в линейную регрессию и корреляцию. Сан-Франциско, Калифорния: WH Freeman; 1976. С. 33–46 [Google Scholar] 28. Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Числовые рецепты на C: искусство научных вычислений (2-е изд.) Издательство Кембриджского университета; 1992 [Google Scholar] 29.Кэнни Дж. Вычислительный подход к обнаружению краев. IEEE Trans Patt Anal Mach Intell 1986; 8: 679–714 [PubMed] [Google Scholar] 30. Цзэн П.Ф., Хирата Т. Улучшение на основе карты расстояний для интерполированных изображений. Lec Not Comp Sc 2003; 2616: 429–449 [Google Scholar] 31. Гонсалес RC, Вудс RE. Цифровая обработка изображений (2-е изд.) Нью-Джерси, Нью-Джерси: Прентис-Холл; 2002 [Google Scholar]Объемное сжатие видео для интерактивного воспроизведения
Comput Vis Image Underst. Авторская рукопись; доступно в PMC 2010 12 января.
Опубликован в окончательной редакции как:
PMCID: PMC2805201
NIHMSID: NIHMS162774
Департамент компьютерных наук и ICES, Техасский университет, Остин, Техас 78712
Аннотация
Мы разрабатываем систему объемного видео поддерживает интерактивный просмотр сжатых изменяющихся во времени объемных объектов (значимые изоповерхности и интервальные объемы). Поскольку размер даже одного объемного кадра в изменяющемся во времени наборе трехмерных данных очень велик, передача и оперативная реконструкция являются основными узкими местами для интерактивной удаленной визуализации изменяющихся во времени объемных и поверхностных данных.Мы описываем схему сжатия для кодирования изменяющихся во времени объемных объектов унифицированным способом, что позволяет производить реконструкцию и рендеринг в режиме онлайн. Чтобы увеличить скорость распаковки и степень сжатия во время выполнения, мы разбиваем объем на небольшие блоки и кодируем только те блоки, которые вносят вклад в изоповерхности и интервальные объемы. Результаты показывают, что наша схема сжатия обеспечивает высокую степень сжатия с быстрой реконструкцией, что эффективно для рендеринга изменяющихся во времени объемных объектов на стороне клиента.
Ключевые слова: Визуализация изменяющегося во времени объема, 3D-видео, сжатие, изоконтурирование, аппаратное ускорение, вейвлет-преобразование . Например, размер набора океанографических данных об изменении температуры, протестированного в этой статье, составляет 237 МБ / кадр (2160 × 960 × 30 с плавающей запятой) × 115 кадров, а набор данных газовой динамики составляет 64 МБ / кадр (256 × 256 × 256 с плавающей точкой). × 144 кадра.Чтобы визуализировать такие изменяющиеся во времени объемные данные, методы объемного рендеринга, и изоконтурирования выполняются кадр за кадром, так что пользователь может перемещаться и исследовать набор данных в пространстве и времени. Оба метода рендеринга имеют свои сильные стороны. В то время как объемный рендеринг может отображать аморфные объемные области, заданные передаточной функцией, с прозрачностью, изоконтурирование может обеспечить геометрическую форму поверхностей, заданную значительными изо значениями. Оба метода можно комбинировать для лучшего понимания всей информации, содержащейся в наборе объемных данных.Например, показывает визуализацию смоделированного взрыва во время формирования галактики посредством визуализации изменяющихся во времени объемов и изоповерхностей.
Интерактивное воспроизведение объемного видео моделированной газовой динамики взрыва.
В то время как современное графическое оборудование обеспечивает очень быстрый объемный и поверхностный рендеринг, передача таких больших данных между серверами данных и просматривающими клиентами может стать узким местом из-за ограниченной пропускной способности сетей. Эффективное управление данными — важный фактор в производительности рендеринга.Чтобы уменьшить размер набора данных, естественно использовать временную и пространственную когерентность в любой схеме сжатия. Однако, поскольку размер данных даже одного кадра очень велик, распаковка во время выполнения также может быть узким местом для интерактивного воспроизведения.
Исходя из этого, мы разработали унифицированную схему сжатия для кодирования изменяющихся во времени объемных объектов. В большинстве случаев мы используем термин признак для обозначения изоповерхности и / или интервального объема, заданного диапазоном скалярных значений.Интервальный том может быть целым. Входы для сжатия: k iso-values iso i , i = 1 .. k , l диапазоны значений [ r a , r b ] i , i = 1 .. l и дискретные изменяющиеся во времени данные объема V . Данные V , содержащие временные шаги T , могут быть представлены как V = { V 1 , V 2 ,…, V T }, где Vt = {fi, j, kt∣i, j, kareindicesofx, y, zcoordinates} — объем на временном шаге t , содержащий значения данных fi, j, kt по индексам i, j, k .Наша основная цель в области сжатия —
унифицированным образом сжать изменяющиеся во времени изоповерхности и интервальные объемы.
уменьшить размер изменяющихся во времени объемных данных с минимальным ухудшением качества изображения.
обеспечивает реконструкцию и рендеринг в реальном времени с аппаратным ускорением графики ПК.
Мы заимствуем идею сжатия MPEG, чтобы эффективно использовать пространственную и временную когерентность в наборах данных. Однако прямое расширение MPEG для сжатия 2D-видео на изменяющуюся во времени изоповерхность и сжатие функций не подходит для достижения наших целей.Поскольку MPEG кодирует и декодирует каждый блок в каждом кадре объемных изменяющихся во времени данных, ненужные области в данных также могут кодироваться и декодироваться.
Мы применяем блочное вейвлет-преобразование с временным кодированием в нашей схеме сжатия. Вейвлет-преобразование широко используется для сжатия 2D и 3D изображений. Обрезая незначительные коэффициенты после вейвлет-преобразования, эти схемы достигают высокой степени сжатия при сохранении минимального искажения изображения. Однако полное преобразование каждого кадра является пустой тратой пространственных и временных ресурсов, поскольку значения функций, не влияющие на данные изоповерхности и объемные характеристики, не нуждаются в кодировании.Кроме того, не нужно обновлять вспомогательные значения, которые со временем претерпевают небольшие изменения. Следовательно, кодирование и декодирование только значимых в пространстве и времени значений вместо полного объема может улучшить как степень сжатия, так и скорость распаковки.
Каждый объемный кадр классифицируется либо как кадр с внутренним кодированием, либо как кадр с прогнозированием. Внутри кодированные кадры могут быть распакованы независимо, в то время как прогнозные кадры отличаются от своих предыдущих кадров. Предполагая, что разные блоки имеют разную временную дисперсию, мы можем отсортировать блоки на основе их временной дисперсии и обрезать незначительные блоки для достижения более высоких степеней сжатия и более высоких скоростей распаковки.
В дополнение к эффективному сжатию также достигается быстрая реконструкция и рендеринг изоповерхностей и объемных объектов. Добавляя исходные ячейки в сжатый поток каждого кадра объема, обозреватель визуализации может построить изоповерхности за минимальное время. Высокая скорость достигается за счет удаления фазы поиска для обнаружения по крайней мере одной ячейки, пересекающейся с каждым компонентом изоповерхности. Поскольку изоповерхность фиксирована, нам нужно хранить только одну затравочную ячейку для каждого компонента изоповерхности, что практически не влияет на степень сжатия.Мы также можем сжать выбранный набор компонентов в изоповерхностях и объемах и их эволюцию, используя метод отслеживания признаков [24]. Реконструированные элементы могут отображаться в реальном времени с помощью графического оборудования ПК.
показывает общую архитектуру нашей интерактивной системы отображения объемного видео. Алгоритм требует, чтобы функции были определены перед сжатием. Эти особенности можно идентифицировать вручную или с помощью средств автоматического определения признаков [18]. Чтобы сэкономить место на диске и преодолеть ограничение пропускной способности ввода-вывода в сетевых системах, серия сжатых кадров считывается с серверов источников данных для просматривающих клиентов.После считывания каждого сжатого кадра он распаковывается в программном обеспечении. Массив восстановленных изображений используется для ускоренного изоконтурирования, а также отправляется в память текстуры в графическом оборудовании для отображения объемных характеристик. Эта архитектура может позволить пользователям исследовать и взаимодействовать с изоповерхностями, встроенными в аморфные объемные объекты в пространстве и времени, что является нашей конечной целью.
Интерактивный объемный конвейер видео и удаленной потоковой передачи и отображения
Остальная часть этого документа организована следующим образом.Сначала описывается сопутствующая работа. Затем в разделе 3 описывается архитектура для отображения объемного видео. В разделе 4 предлагается схема объемного сжатия видео, поддерживающая интерактивную декомпрессию. В разделе 5 описана наша схема интерактивного просмотра сжатых изменяющихся во времени функций. Результаты экспериментов описаны в разделе 6. Наконец, в разделе 7 мы даем заключение.
2 Сопутствующие работы
Визуализация изменяющихся во времени объемных данных была сложной задачей.Сжатие, временные структуры данных и высокопроизводительные системы визуализации были введены, чтобы справиться с огромными размерами данных и высокими требованиями к вычислениям.
Сжатие
Сжатие чрезвычайно полезно для обработки больших объемов данных, особенно для передачи данных с серверов просматривающим клиентам. Поскольку научные данные, как правило, очень большие и имеют много избыточности, люди предпочитают использовать сжатые данные для эффективного использования памяти и пропускной способности ввода-вывода.Разработан ряд алгоритмов сжатия изображения и поверхности.
Работы по единому разрешению и прогрессивному сжатию триангулированных поверхностей (например, изоповерхностей) включают статьи [27,12]. Схема сжатия, специализированная для изоповерхностей [29], использует уникальное свойство изоповерхности, которое требует кодирования только значительных ребер и значений функций, определенных на вершине.
Большинство методов сжатия изображений ориентированы на достижение наилучшего коэффициента сжатия с минимальным искажением реконструированных изображений.JPEG и MPEG [6] разработаны для сжатия неподвижных изображений и 2D-видеоданных с контролируемым размером и компенсацией искажений. Встроенные алгоритмы кодирования, такие как встроенный вейвлет нулевого дерева (EZW) [21] и разделение наборов в иерархических деревьях (SPIHT) [19], полезны для приложений прогрессивной передачи и мультимедиа.
Для сжатия трехмерных изображений Ihm et al. [11] описал схему трехмерного сжатия на основе вейвлетов для видимых человеческих данных и позже расширил ее до сжатия трехмерных изображений RGB для интерактивных приложений, таких как рендеринг светового поля и наложение трехмерной текстуры [2].Коэффициенты сжатия могут быть улучшены путем захвата и кодирования только важных структур и функций в наборе данных [1,16]. В этих схемах сжатия основной целью является быстрый произвольный доступ к данным при сохранении высоких степеней сжатия. Это позволяет интерактивно отображать наборы данных большого объема [9].
Guthe и Straser [8] применили алгоритм MPEG к изменяющимся во времени объемным данным, используя вейвлет-преобразования. Они сравнивают эффекты компенсации движения и использования различных базисных функций вейвлета.Lum et al. [14] использует оборудование текстур как для рендеринга, так и для распаковки. Поскольку данные передаются в сжатом формате между различными системами памяти, время ввода-вывода значительно сокращается.
Структуры данных на основе времени
Дерево пространственно-временного разделения (TSP) было введено и ускорено позже за счет использования оборудования трехмерного наложения текстур [5] для быстрого объемного рендеринга изменяющихся во времени полей. Эффективность достигается за счет пропуска незначительных операций визуализации и повторного использования визуализированных изображений на предыдущем временном шаге.
Шен [22] предложил структуру данных Temporal Hierarchical Index (THI) Tree для изоконтурирования изменяющихся во времени данных с единым разрешением путем расширения своего алгоритма ISSUE [23]. Дерево THI обеспечивает компактную структуру поиска, сохраняя при этом оптимальное время поиска. Следовательно, сокращаются дорогостоящие дисковые операции для получения структур поиска. Sutton et al. [26] предложил Temporal Branch-on-Need Tree путем расширения октодеревьев для минимизации ненужного доступа к вводу-выводу и поддержки извлечения изоповерхности вне ядра в изменяющихся во времени полях.
Шамир и др. [20] разработали адаптивную структуру данных с несколькими разрешениями для многоугольных сеток, зависящих от времени, под названием T-DAG (Time-Direct Acyclic Graph). T-DAG — это компактное представление, которое поддерживает запросы формы (временной шаг, допустимость ошибок) и возвращает приближенную сетку для этого временного шага, удовлетворяющую допуску ошибок.
Высокопроизводительные системы визуализации
Ма и Кэмп [15] описывают удаленную систему визуализации в среде глобальной сети для визуализации наборов данных, изменяющихся во времени.Современное графическое оборудование позволяет в реальном времени выполнять объемный и изоповерхностный рендеринг [28] и декомпрессию [14].
Извлечение изоповерхностей
В прошлом большое количество исследований было посвящено быстрому извлечению изоповерхностей из трехмерных статических объемных данных. Алгоритм Marching Cubes [13] посещает каждую ячейку в объеме и выполняет соответствующую локальную триангуляцию для создания изоповерхности. Чтобы избежать посещения ненужных ячеек, разработаны ускоренные алгоритмы [4], минимизирующие время на поиск участвующих ячеек.
Алгоритм распространения контуров используется для эффективного извлечения изоповерхностей [3,10]. Учитывая начальную ячейку, которая содержит компонент изоповерхности, оставшуюся часть компонента можно проследить путем распространения контура. Это свойство значительно сокращает пространство и время, необходимые для поиска ячеек, содержащих изоповерхность, за счет использования небольшого количества исходных ячеек. Методы множественного разрешения [7] и зависимости от вида [30] полезны для уменьшения количества треугольников на изоповерхности.
3 Интерактивное объемное видео
Как и широко используемые системы 2D-видео, система объемного видео отображает последовательность трехмерных изображений во времени, кадр за кадром.Находясь в 2D-видео, пользователи могут только пассивно смотреть на постоянно обновляемые 2D-изображения, объемное видео или изменяющаяся во времени система визуализации объема позволяет им исследовать и перемещаться по 3D-данным как в пространстве, так и во времени. Учитывая, что большинство научных симуляций генерируют динамические объемные данные, объемные видеосистемы особенно полезны для анализа научных данных.
Наивный способ отображения изменяющихся во времени данных трехмерного объема — это повторное считывание каждого кадра с сервера данных и визуализация объема с заданными параметрами визуализации.Поскольку большинство изменяющихся во времени наборов научных данных очень большие и имеют высокую пространственную и временную когерентность, естественно применять сжатие для уменьшения накладных расходов на хранение и времени передачи. Однако распаковка во время выполнения данных, закодированных стандартными схемами статического и изменяющегося во времени сжатия изображения, может стать узким местом при воспроизведении объемного видео в реальном времени, поскольку они обычно разбивают изображение на блоки и декодируют каждый блок во время распаковки. Во время сжатия мы упорядочиваем блоки в зависимости от их значимости и кодируем только существенно изменяющиеся блоки.Это увеличивает скорость распаковки во время выполнения, поскольку мы ограничили количество блоков для декодирования.
Применяется двухэтапная стратегия для обеспечения интерактивной навигации и исследования очень больших объемов данных, зависящих от времени. На первом этапе на стороне сервера большой объем, зависящий от времени, анализируется и обрабатывается на высокопроизводительном сервере, так что результаты этой объемной обработки представляют собой промежуточное объемное представление интересных характеристик (изоповерхность, объем) с различным разрешением, зависящее от времени. в пределах диапазона) данных, сгенерированных и сохраненных в сжатом формате.Промежуточное представление с несколькими разрешениями позволяет найти компромисс между интерактивностью и визуальной точностью для второго, интерактивного этапа просмотра. На втором этапе на стороне клиента объемное видео декодируется и воспроизводится браузером интерактивной визуализации, который может быть доступен на стандартной настольной рабочей станции, оснащенной 3D-видеокартой. В отличие от стандартного видеопроигрывателя, браузер визуализации может обеспечивать определенные уровни интерактивности, такие как динамическое изменение параметров просмотра, изменение условий освещения и настройка функций передачи цвета и непрозрачности, в дополнение к воспроизведению объемного видео по времени вместе с некоторыми пользователями. заданный путь полета в пространстве и времени.
4 Схема сжатия
В этом разделе мы описываем унифицированную схему для одновременного сжатия как изменяющихся во времени изоповерхностей, так и объемных объектов. Кодируя только значимые значения функции на основе связанных весов с использованием вейвлет-преобразования, мы можем достичь высоких степеней сжатия. Однако простое кодирование функций требует оперативного извлечения изоповерхностей на стороне клиента. Чтобы ускорить процесс извлечения поверхности, мы вставляем посевные клетки в рамки сжатого объема.
4.1 Сжатие
Набор входных данных представляет собой набор данных по объему, зависящий от времени, V = { V 1 , V 2 ,…, V T } с k isvalues iso 1 ,…, iso k и l диапазоны значений r 1 = [ r a , r b ] 1 ,…, r l = [ r a , r b ] l .Каждый кадр тома классифицируется как кадр с внутренним кодированием или кадр с прогнозированием. Для каждого значения и диапазона восстановленное качество может быть указано как пороговое значение для вейвлет-коэффициентов и другое пороговое значение для блоков в кадрах предсказания, так что вейвлет-коэффициенты или блоки, не удовлетворяющие этому значению, усекаются. Критерии усечения приведены в шагах алгоритма сжатия ниже. Весь набор данных представлен как V = {{ I 1 , P 11 , P 12 ,…, P 1 p 1 },…, { I N , P N 1 , P N 2 ,…, P N pN }} где I i — это внутрикодированный кадр во временной группе i — th , а P ij — это прогнозный кадр j — th во временной группе i — th .
Предполагая, что между последовательными кадрами есть только небольшие изменения, вейвлет-преобразование изменений вместо целых кадров дает более высокие коэффициенты сжатия и меньшее время декомпрессии. Следовательно, сжатие внутрикадрового кадра не зависит от других кадров, в то время как сжатие прогнозируемого кадра зависит от предыдущих кадров в той же временной группе. Общий алгоритм сжатия показан на. Обратите внимание, что сжатие выполняется для каждого тома, и кодируются только важные значения, влияющие на характеристики.Все трехмерные кадры раскладываются на блоки 4 × 4 × 4, и вейвлет-преобразование выполняется для каждого блока, вносящего вклад в указанные функции в объеме. Шаги алгоритма сжатия следующие:
Общий алгоритм сжатия
разность объемов: ΔVk = Vk − Vk − 1 ′ , где V k — исходное изображение k -го кадра и Vk − 1 ′ — восстановленное изображение сжатого объема V k −1 .Если V k является кадром с внутренним кодированием, мы предполагаем Vk − 1 ′ = 0.
вейвлет-преобразование : W Δ V k = вейвлет-преобразование Δ V k . Вычислить коэффициенты c 1 ,…, c m , представляющие Δ V k в трехмерном базисе вейвлета Хаара.
классификация Каждый вейвлет-коэффициент c и блок b классифицируются как незначительные или значимые. c и b далее классифицируются в зависимости от того, каким функциям они способствуют. c и / или b могут принадлежать более чем одному объекту. В таких случаях выживаемость c или b зависит от самого высокого взвешенного объекта, который их содержит.
усечение блоков Блок, который не влияет на характеристики или имеет очень небольшие изменения во времени, считается несущественным блоком. Обрезая незначительные блоки, мы можем добиться более высоких степеней сжатия и можем контролировать время восстановления объема.Чтобы идентифицировать блоки, вносящие вклад в i -й признак и имеющие незначительные изменения, сумма квадратов коэффициентов сравнивается с пороговым значением λ i . Если сумма меньше λ i , блок обрезается. Для кодирования усеченного блока в карте значимости блока назначается только один бит.
усечение вейвлет-коэффициентов : объект i , подлежащий сжатию, имеет собственный вес, представленный как пороговое значение τ i .Установив пороговое значение, можно управлять восстановленным качеством конкретной функции. Если вейвлет-коэффициент c , связанный с i -м признаком, меньше, чем i , коэффициент обрезается до нуля.
кодирование : общая схема кодирования показана в. После выполнения усечения вейвлет-коэффициентов на основе веса каждого признака мы берем выживающие коэффициенты и кодируем их. Кодирование выполняется для каждого блока, в результате получается последовательность закодированных блоков.Мы классифицируем 64 коэффициента в блоке как один коэффициент уровня 0, 7 коэффициентов уровня 1 и коэффициенты 8 × 7 уровня 2, чтобы воспользоваться преимуществами иерархической структуры блока.
Предлагаемая схема кодирования для поддержки быстрой декомпрессии и высоких степеней сжатия
В заголовке кадра сохраняется поток битов, представляющий значимость каждого блока, чтобы указать, является ли блок, соответствующий каждому биту, нулевым блоком или нет. Это позволяет избежать дополнительных накладных расходов на хранилище для незначительных блоков.Каждому блоку в последовательности назначается один бит. Затем для каждого значимого блока мы сохраняем 8-битную карту, показывающую, равны ли один коэффициент уровня 0 и семь коэффициентов уровня 1 нулю или нет. Затем у нас есть еще одна 8-битная карта, показывающая, имеют ли каждый восемь подблоков 2 × 2 × 2 ненулевые вейвлет-коэффициенты, за которой следует карта значимости для представления ненулевых коэффициентов уровня 2. После сохранения карт значимости коэффициентов уровня 2 фактические значения ненулевых вейвлет-коэффициентов сохраняются по порядку.Мы использовали два байта для хранения каждого значения коэффициента. Сжатие без потерь применяется для улучшения сжатия.
4.2 Вставка исходных ячеек
Чтобы позволить клиентам просмотра быстро извлекать изоповерхности, закодированные в томе, исходные ячейки присоединяются к сжатому потоку каждого кадра. Исходная ячейка гарантированно пересекается со связным компонентом изоповерхности. Выполняя поверхностное размножение из заданных семенных клеток, мы можем избежать посещения ненужных ячеек и сэкономить время экстракции.Поскольку для каждого компонента изоповерхности требуется только одна начальная ячейка, размер начальных ячеек незначителен, и поисковые структуры, такие как октодеревья и деревья интервалов, не требуются. Следовательно, время извлечения изоповерхности зависит только от количества треугольников независимо от размера объема.
4.3 Декомпрессия во время выполнения
Поскольку у нас есть последовательность закодированных вейвлетом объемов W Δ V k , мы можем получить приблизительное изображение Vk ′ путем декодирования и выполнения обратного вейвлет-преобразования.В частности, ΔVk ′ = обратное преобразование (WΔVk) и Vk ′ = Vk − 1 ′ + ΔVk. Для кадра с внутренним кодированием V i , Vi − 1 ′ = 0, и мы можем получить Vi ′ прямо из ΔVi ′ без зависимости от других кадров. После восстановления V i последующие прогнозные кадры могут декодироваться кадр за кадром, пока не будет достигнут следующий кадр с внутренним кодированием.
Распаковка основана на поблочном декодировании. В кадрах с внутренним кодированием каждый блок должен быть распакован с помощью полного обратного вейвлет-преобразования.С другой стороны, в прогнозных кадрах обновляются только существенно изменяющиеся блоки, так что оно может максимально точно аппроксимировать фактическое изображение при минимальном времени декомпрессии. Конкретный алгоритм декодирования следующий. Используя карту значимости блока, мы можем идентифицировать каждый значимый блок и соответствующие ему кодированные блоки. Для каждого закодированного блока выполните следующие действия: Прочтите 8 бит. b11,…, b81, чтобы решить, равны ли один коэффициент уровня 0 и семь коэффициентов уровня 1 нулю.Далее прочтите 8bit b12,…, b82, чтобы решить, имеют ли каждые восемь субблоков ненулевое значение или нет. Если bk2, где k = 1,…, 8, устанавливается как 1, читать 8 бит c1k,…, c8k, чтобы определить, какие коэффициенты k -го подблока отличны от нуля. На картах значимости, прочитанных выше, мы можем по порядку считывать фактические ненулевые коэффициенты. Когда все значения коэффициентов определены, выполняется обратное преобразование, чтобы получить фактические значения данных, и соответствующий блок обновляется.
После того, как значимые значения функции декодированы, мы выполняем извлечение изоповерхностей. Для каждого значимого изозначения у нас есть начальный набор, и, следовательно, мы можем быстро выполнить вышеуказанное извлечение.
5 Интерактивный просмотр
Хотя степень сжатия является важным фактором повышения производительности ввода-вывода в памяти и сетевых системах, не менее важно, чтобы обозреватель визуализации мог читать и интерактивно отображать сжатые потоки наборов данных с разным разрешением и изменяющимися во времени .
5.1 Рендеринг изоповерхности с несколькими разрешениями
Поскольку изоповерхность часто содержит много треугольников, для экономии времени извлечения и рендеринга необходимы методы множественного разрешения в качестве компромисса с визуальной точностью. Одной из сильных сторон вейвлет-преобразований является то, что они предоставляют сжатые представления с разным разрешением в согласованном формате.
В нашем блочном вейвлет-преобразовании есть 3 уровня, состоящие из одного 0-го уровня, семи 1-го уровня и пятидесяти шести коэффициентов 2-го уровня.Коэффициент 0-го уровня обеспечивает среднее значение 4 × 4 × 4 ячеек после фильтрации нижних частот. Коэффициенты 0-го уровня и 1-го уровня вместе дают приблизительные промежуточные значения, усредняющие 2 × 2 × 2 ячейки. Когда быстрое извлечение и рендеринг изоповерхностей важнее точности, клиент может взять только коэффициенты 0-го уровня и / или 1-го уровня и восстановить объем с более низким разрешением. Поскольку реконструированный объем с низким разрешением является хорошим приближением к исходному объему, не только извлеченная изоповерхность является хорошим приближением исходной изоповерхности, но также сокращается количество извлеченных треугольников.Этот процесс имеет эффект низкочастотной фильтрации объема, которая может удалить шум и артефакты, возникающие при сжатии с потерями. показывает три изображения, визуализированных с использованием одних и тех же объемных данных, но на разных уровнях изоповерхности.
Три разных уровня изоповерхности. Количество изоповерхностных треугольников и время извлечения для уровня 0 (слева), уровня 1 (в центре) и уровня 2 (справа) составляют (11878, 204 мс), (41624, 625 мс) и (207894, 3110 мс).
5.2 Комбинированный рендеринг изоповерхности и объемных данных
Мы комбинируем изоповерхностный и объемный рендеринг, чтобы воспользоваться преимуществами обоих методов.Мы берем изоповерхность как область, которую нам нужно рассмотреть более подробно, с непрозрачным или полупрозрачным объемом в пространстве объектов. Результаты рендеринга отображаются и сравниваются в формате. В этом наборе данных извлечение изоповерхности обеспечивает заштрихованную поверхность, представляющую конкретное значение температуры. Объемный рендеринг показывает температуру вокруг изоповерхности. Комбинируя оба метода, визуальная информация, содержащаяся в рендеринге, улучшается.
Визуализация набора океанографических данных об изменении температуры.Слева вверху: рендеринг изоповерхности, слева внизу: рендеринг объема, справа: комбинированный рендеринг изоповерхности и объема.
Мы протестировали нашу работу на реализации, основанной на OpenGL. OpenGL дает нам возможность выполнять тесты глубины и поддерживать карту глубины. Мы используем это для единообразной визуализации изоповерхности и объема. Поэтому мы устанавливаем изоповерхность полностью непрозрачной и визуализируем ее с помощью OpenGL с включенным тестом глубины. Затем мы визуализируем набор трехмерных текстурированных полигонов, нарезанных из объема в порядке от задней части к передней.Это согласуется с рекомендациями документации OpenGL [17].
Во время рендеринга изоповерхности мы строим карту глубины, которая используется во время рендеринга объема. Хотя изоконтурирование в целом требует большого количества времени, у нас уже есть семена, необходимые для выполнения изоконтурирования набора семян. Таким образом достигается быстрая реконструкция изоповерхности. Когда мы выполняем объемную визуализацию, чтобы получить правильные результаты прозрачности, мы визуализируем полигоны в отсортированном порядке. Хотя, как правило, на выполнение сортировки по полигонам уходит много времени, возможность трехмерного отображения текстур видеокарты Nvidia 3 помогает с этим справиться.Объемные данные хранятся в памяти текстур видеокарты. Мы создаем многоугольники с помощью простого инкрементального алгоритма, делая срезы по объему. Эти полигоны визуализируются с соответствующими значениями текстуры в 3D-памяти. Интерактивная карта передаточной функции для управления значениями цвета и непрозрачности используется для получения требуемых изображений. Если пользователь вращает объем, нам нужно обновить направление нарезки. Чтобы получить немного лучшую производительность, мы отключаем построение буфера глубины (используя glDepthMask (0)) при рендеринге объема, поскольку мы уверены, что рендеринг полигонов будет по порядку, и поскольку все полигоны, отрендеренные ранее, непрозрачны.
6 Результаты экспериментов
Результаты сжатия и рендеринга были рассчитаны на ПК, оснащенном процессором Pentium III 800 МГц, 512 МБ оперативной памяти и графической картой NVidia GeForce 3 с 128 МБ памяти для текстур. Мы использовали стандартные функции OpenGL для объемного рендеринга на основе трехмерного наложения текстур.
предоставляет информацию о наших наборах тестовых данных. Первый набор данных генерируется в результате компьютерного космологического моделирования формирования крупномасштабных структур во Вселенной.Поскольку функции в наборе данных претерпели незначительные изменения в последних нескольких кадрах, мы предоставили все наши результаты сжатия для этого набора данных на основе первых 100 кадров. Второй набор данных создается с помощью океанографического моделирования и представляет изменения температуры в океане с течением времени. Исходная модель имеет приблизительное разрешение 1/6 градуса (2160 на 960) по широте и долготе и несет информацию на 30 уровнях глубины. Поскольку исходное разрешение данных слишком велико для аппаратного объемного рендеринга, мы прорежем его до 512 × 256 × 32 с помощью субдискретизации и взяли каждый третий кадр.Третий набор данных получен при моделировании динамики гемоглобина. Моделирование сгенерировало последовательность файлов pdb гемоглобина с тридцатью временными шагами, и объемы электронной плотности вычисляются из каждого файла pdb.
Таблица 1
Информация о наборах данных, изменяющихся во времени
| Данные | Рез. | тип | #frm | 1 frm size |
|---|---|---|---|---|
| Gas | 256 × 256 × 256 | float | 144 | 64MB |
| 412 Ocean | float | 39 | 16MB | |
| Hemoglobin | 128 × 128 × 128 | float | 30 | 8MB |
Для тестирования производительности мы закодировали только наши высокотемпературные регионы. в диапазоне от 21.47 и 36,0 (градус Цельсия) в наборе океанографических данных о температуре и областях с высокой плотностью в диапазоне от 0,23917 до 3,26161 в наборе данных газовой динамики, как показано на и. После кодирования вейвлет-коэффициентов мы использовали gzip для сжатия без потерь.
Набор данных по газовой динамике. Исходный объем (слева), восстановленный объем со степенью сжатия 148: 1 (в центре) и степенью сжатия 301: 1 (справа).
Набор океанографических данных об изменении температуры. Исходный объем (слева) и восстановленный объем со степенью сжатия 183: 1 (справа).
и показывают время восстановления, среднеквадратичную ошибку (RMSE) и степень сжатия, изменяющуюся во времени в наборах данных газовой динамики и океанографии. Время восстановления включает время чтения с диска, gunzip, и декодирование вейвлет-коэффициентов. Среднеквадратичная ошибка среднего была рассчитана с использованием только тех значений функций, которые способствовали характеристикам. Степень сжатия была рассчитана путем сравнения размера исходных изменяющихся во времени объемных данных и функционально сжатых данных, закодированных с применением нашего сжатия с потерями и gzip.Как вы можете видеть в таблицах, время восстановления P-кадра намного меньше, чем у I-кадра, в то время как степень сжатия P-кадра намного выше, чем у I-кадра. Причина этого в том, что наша схема сжатия кодирует только существенно изменяющиеся блоки в P-кадрах.
Таблица 2
Характеристики сжатия по набору данных газовой динамики (*: исходный диапазон плотности [0., 8065,299])
| Средняя степень сжатия — 148: 1, RMSE — 0,108 | ||||||
|---|---|---|---|---|---|---|
| Номер рамы | Recon.время | СКО * | Сравн. отношение | |||
| 1 (I) | 687 мс | 0,105 | 40: 1 | |||
| 2 (P) | 177 мс | 0,131 | 371427 | 3271 мс | 0,101 | 182: 1 |
| 4 (P) | 235 мс | 0,103 | 234: 1 | |||
| — Среднее сжатие 1 — Среднее сжатие139 | ||||||
|---|---|---|---|---|---|---|
| Рама № | Развед. время | СКО * | Сравн. соотношение | |||
| 1 (I) | 489 мс | 0,127 | 70: 1 | |||
| 2 (P) | 141 мс | 0,156 | 988: 1 | 207 мс | 0,130 | 422: 1 |
| 4 (P) | 188 мс | 0,134 | 516: 1 | |||
Таблица 3
Температура сжатия (исходные данные для океанографических данных) диапазон [−2.0, 36,0])
| Средняя степень сжатия — 183: 1, RMSE — 0,090 | ||||
|---|---|---|---|---|
| № кадра | Развед. время | СКО ** | Сравн. отношение | |
| 1 (I) | 124 мс | 0,076 | 72: 1 | |
| 2 (P) | 76 мс | 0,087 | 273: 1 | 96 мс | 0,089 | 226: 1 |
| 4 (P) | 86 мс | 0.091 | 223: 1 | |
| Средняя степень сжатия — 348: 1, RMSE — 0,177 | ||||||
|---|---|---|---|---|---|---|
| Frame # | Recon. время | СКО ** | Сравн. Соотношение | |||
| 1 (I) | 106 мс | 0,157 | 103: 1 | |||
| 2 (P) | 57 мс | 0,169 | 615: 1 | 65 мс | 0,175 | 493: 1 |
| 4 (P) | 64 мс | 0.178 | 482: 1 | |||
В этом примере мы сравниваем нашу схему кодирования на основе функций (FBE) со схемой кодирования полного объема (FVE). Поскольку FBE кодирует только значения, вносящие вклад в указанные функции, время распаковки и степень сжатия значительно улучшаются по сравнению со схемами, кодирующими полные тома. В то время как время передачи и восстановления объемных и изоповерхностных характеристик сокращается за счет кодирования FBE, рендеринг на стороне клиента значительно ускоряется за счет использования графического оборудования ПК.
Сравнение производительности различных схем кодирования. Хотя степень сжатия (a) и (b) одинакова (181: 1), качество восстановленного изображения с использованием (a) лучше, чем (b). Среднеквадратичное значение (a) равно 0,110 и (b) равно 0,131. (a) Кодируются только значения, вносящие вклад в функции. (b) Каждое значение в объеме закодировано.
и показывают типичный кадр набора данных газовой динамики, сжатый с различными степенями сжатия. и показать течение двух изоповерхностей определенных температур.показывает увеличенный вид того же набора томов, визуализированных в. Мы заметили, что хорошее визуальное качество сохраняется даже при таких коэффициентах масштабирования и высоких степенях сжатия. Хотя увеличенное изображение объема, сжатого с коэффициентом сжатия 148: 1, визуально почти не отличается от оригинала, мы получаем лишь несколько артефактов при коэффициенте сжатия 301: 1. и показывают, что аналогичные результаты были получены при применении нашей схемы сжатия и рендеринга к набору океанографических данных. Мы использовали изоповерхности для отслеживания движения воды с определенной температурой и полупрозрачную объемную область для представления окружающей температуры.Эти рисунки демонстрируют силу нашей схемы, позволяющую интерактивно визуализировать определенные интересующие области с высококачественными изоповерхностями, окруженными соответствующими объемными данными. Временные результаты рендеринга представлены в формате.
Набор данных по газовой динамике. Увеличенные изображения из.
Набор океанографических данных об изменении температуры. Увеличенные изображения из.
Таблица 4
Временные результаты визуализации изоповерхностей с аморфными объемными элементами в одном кадре: (имя набора данных, время загрузки трехмерной текстуры, время извлечения изоповерхностей, количество треугольников в изоповерхностях, время визуализации изоповерхностей, время объемной визуализации)
| Набор данных | Нагрузка | Внеш.Время | Tri # | Изоповерхность | Объем | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Газ | 701 мс | 1703 мс | 135362 | 312 мс | 422 мс | 312 мс | 422 мс | | 281 мс | |
показывает результат сжатия при моделировании динамики гемоглобина. Объемный рендеринг был применен к каждому сжатому объемному кадру, и мы измерили частоту кадров.Мы достигли высокой степени сжатия (110: 1) и высокой частоты кадров (6,3 кадра / сек) при приемлемом качестве восстановления.
Моделирование динамики гемоглобина. Слева: исходный объем, посередине: увеличенный исходный объем, увеличенный восстановленный объем справа с коэффициентом сжатия 110: 1).
Как правило, частота кадров при объемном воспроизведении видео в основном зависит от разрешения объемов и количества треугольников в извлеченных изоповерхностях. Размер рендеринга также является важным фактором, поскольку рендеринг объема на основе текстуры зависит от операций с пикселями.
Хотя кодирование на основе вейвлетов может привести к некоторым потерям в объемах, а также в топологии реконструированных изоповерхностей, мы можем достичь очень высоких степеней сжатия с приемлемым ухудшением качества.
7 Заключение
Мы описываем схему сжатия с потерями для кодирования изменяющихся во времени изоповерхностей с аморфными объемными характеристиками, заданными диапазонами скалярных значений. Поскольку большие изменяющиеся во времени объемные данные обладают значительной согласованностью, сжатие необходимо для экономии места для хранения, сокращения времени передачи и повышения производительности визуализации изменяющихся во времени данных.Мы достигли нескольких наших целей: (i) высокая степень сжатия с минимальной деградацией изображения, (ii) быстрая декомпрессия за счет усечения незначительных блоков и вейвлет-коэффициентов, и (iii) интерактивный рендеринг на стороне клиента сжатых изоповерхностей с разным разрешением и объемных объектов. Следовательно, наша схема сжатия полезна для интерактивной навигации и исследования изменяющихся во времени изоповерхностей с аморфными объемными элементами, находящихся на локальных и / или удаленных серверах данных.
Благодарности
Ранняя версия этой статьи появилась в VolVis02 [25].Мы благодарны Энтони Тейну, разработавшему инструмент объемного рендеринга CCV (Volume Rover) и библиотеку, а также Сяоюй Чжан и Джон Виггинс за написание кода объемного молекулярного размытия. Космологическое моделирование было выполнено Уго Мартелем, Полом Р. Шапиро и Марсело Альваресом из группы исследования образования галактик и межгалактической среды в Юта-Остине. Данные океанографического моделирования были предоставлены профессором Детлефом Штаммером из отдела исследований физической океанографии Океанографического института Скриппса в рамках проекта Национального партнерства по развитию передовой вычислительной инфраструктуры.Динамика гемоглобина (файлы pdb) была предоставлена Дэвидом Гудселлом из Исследовательского института Скриппса.
Эта работа была частично поддержана грантами NSF ACI-9982297, CCR-9988357, грантом DOE-ASCI BD4485-MOID от LLNL / SNL и грантом UCSD 1018140 в рамках NSF-NPACI, Interactive Environments Thrust и гранта от Compaq для кластера ПК со 128 узлами.
Ссылки
1. Bajaj C, Ihm I, Park S. Сжатие больших объемов данных, специфичное для визуализации. Proc. Тихоокеанской графики; Токио, Япония.2001. С. 212–222. [Google Scholar] 2. Баджадж Чандраджит, Ихм Инсунг, Парк Санхун. Сжатие 3D-изображений RGB для интерактивных приложений. ACM-транзакции на графике. 2001. 20 (1): 10–38. [Google Scholar] 3. Баджадж Чандраджит, Паскуччи Валерио, Шикоре Даниэль Р. Быстрое изоконтурирование для улучшения интерактивности. Предыстория симпозиума 1996 г. по объемной визуализации. 1996: 39–46. [Google Scholar] 4. Cignoni P, Marino P, Montani E, Puppo E, Scopigno R. Ускорение извлечения изоповерхностей с использованием интервальных деревьев.IEEE Transactions по визуализации и компьютерной графике. 1997: 158–170. [Google Scholar] 5. Эллсуорт Дэвид, Чан Лин-Джен, Шен Хань-Вэй. Ускорение рендеринга аппаратного объема, зависящего от времени, с использованием деревьев tsp и показателей ошибок на основе цвета. Труды Симпозиума по визуализации и графике. 2000: 119–128. [Google Scholar] 6. Ле Галль Дидье. MPEG: стандарт сжатия видео для мультимедийных приложений. Коммуникации ACM. 1991. 34 (4): 46–58. [Google Scholar] 7. Герстнер Томас, Пахарола Ренато.Сохранение топологии и контролируемая топология, упрощающая извлечение изоповерхностей с разным разрешением. В: Эртл Т., Хаманн Б., Варшней А., редакторы. Proceedings Visualization 2000. 2000. pp. 259–266. [Google Scholar] 8. Гуте Стефан, Штразер Вольфганг. Декомпрессия и визуализация анимированных объемных данных в реальном времени. Визуализация IEEE. 2001: 349–356. [Google Scholar] 9. Guthe Stefan, Wand Michael, Gonser Julius, Straßer Wolfgang. Интерактивный рендеринг больших объемов данных. Труды конференции по визуализации IEEE.2002: 54–60. [Google Scholar] 10. Хауи CT, Блэк EH. Алгоритм распространения сетки для построения изоповерхностей. Форум компьютерной графики. 1994. 13 (3): 65–74. [Google Scholar] 11. Ihm I, Park S. Схема трехмерного сжатия на основе вейвлетов для интерактивной визуализации очень больших объемов данных. Труды графического интерфейса. 1998: 107–116. [Google Scholar] 12. Ходаковский Андрей, Шредер Петер, Свелденс Вим. Прогрессивное сжатие геометрии. В: Akeley Kurt., Редактор. Siggraph 2000, Труды по компьютерной графике.ACM Press / ACM SIGGRAPH / Эддисон Уэсли Лонгман; 2000. С. 271–278. [Google Scholar] 13. Лоренсен В.Е., Клайн Х. Марширующие кубики: алгоритм построения трехмерной поверхности с высоким разрешением. ACM SIGGRAPH. 1987: 163–169. [Google Scholar] 14. Лум Эрик Б., Ма Кван-Лю, Клайн Джон. Аппаратное обеспечение текстур помогло визуализировать изменяющиеся во времени объемные данные. Визуализация IEEE. 2001: 263–270. [Google Scholar] 15. Ма Кван-Лю, Кэмп-Дэвид М. Высокопроизводительная визуализация изменяющихся во времени объемных данных в состоянии глобальной сети.Суперкомпьютерные вычисления. 2000 [Google Scholar] 16. Мачираджу Рагху, Чжу Чжифань, Фрай Брайан, Мурхед Роберт. Структурно-значимое представление структурированных наборов данных. IEEE Transactions по визуализации и компьютерной графике. 1998. 4 (2): 117–132. [Google Scholar] 18. Пфистер Ханспетер, Лоренсен Билл, Баджадж Чандраджит, Киндлманн Гордон, Шредер Уилл, Авила Лиза Соберайски, Мартин Кен, Мачираджу Рагу, Ли Джинхо. Передаточная функция запекания. IEEE Transactions по компьютерной графике и приложениям. 2001. 21 (3): 16–22.[Google Scholar] 19. Саид Амир, Перлман Уильям А. Новый быстрый и эффективный кодек изображений, основанный на разделении множеств в иерархических деревьях. IEEE Transactions on Circuits and Systems for Video Technology. 1996; 6: 243–250. [Google Scholar] 20. Шамир А., Паскуччи В., Баджадж К. Протокол конференции IEEE по визуализации 2000 г. Солт-Лейк-Сити: Юта; 2000. Динамические сетки с разным разрешением и произвольными деформациями; С. 423–430. [Google Scholar] 21. Шапиро Дж. Кодирование встроенных изображений с использованием нулевых деревьев вейвлет-коэффициентов.Транзакции IEEE по обработке сигналов. 1993. 41 (12): 3445–3462. [Google Scholar] 22. Шен Хань-Вэй. Извлечение изоповерхностей в изменяющихся во времени полях с использованием временного иерархического дерева индексов. Визуализация IEEE. 1998: 159–166. [Google Scholar] 23. Шен Хан-Вэй, Хансен Чарльз Д., Ливнат Ярден, Джонсон Кристофер Р. Изоповерхность в пространстве с максимальной эффективностью (ВЫПУСК) В: Ягель Рони, Нильсон Грегори М., редакторы. IEEE Visualization ’96. 1996. С. 287–294. [Google Scholar] 24. Сильвер Д., Ван Х. Отслеживание и визуализация турбулентных трехмерных объектов.IEEE Transactions по визуализации и компьютерной графике. 1997. 3 (2): 129–141. [Google Scholar] 25. Сон Бон-Су, Баджадж Чандраджит, Сиддаванахалли Винай. Объемное сжатие видео на основе функций для интерактивного воспроизведения. Симпозиум IEEE / SIGGRAPH по объемной визуализации и графике. 2002: 89–96. [Google Scholar] 26. Саттон Филип М., Хансен Чарльз Д. Извлечение изоповерхностей в изменяющихся во времени полях с использованием временного дерева ветвей по необходимости (T-BON) В: Эберт Дэвид, Гросс Маркус, Хаманн Бернд, редакторы. IEEE Visualization ’99.Сан-Франциско: 1999. С. 147–154. [Google Scholar] 27. Таубин Габриэль, Россиньяк Ярек. Геометрическое сжатие с помощью топологической хирургии. ACM-транзакции на графике. 1998. 17 (2): 84–115. [Google Scholar] 28. Вестерманн Р., Томас Э. Эффективное использование графического оборудования в приложениях объемного рендеринга. СИГГРАФ. 1998: 169–177. [Google Scholar] 29. Zhang X, Bajaj C, Blanke W. Масштабируемая изоповерхностная визуализация массивных наборов данных на кластерах детских кроваток. Материалы симпозиума IEEE по параллельной визуализации и визуализации больших данных и графике.2001: 51–58. [Google Scholar] 30. Чжан Сяоюй, Баджадж Чандраджит, Рамачандран Виджая. Параллельная и внешняя визуализация изоконтура, зависящая от вида, с использованием случайного распределения данных. Совместный симпозиум Eurographics-IEEE TCVG по визуализации. 2002: 9–18. [Google Scholar]Объемные процедурные модели для представления формы
https://doi.org/10.1016/j.gvc.2021.200018Получить права и контентОсновные моменты
- •
Разработал грамматику и язык программирования для объемного моделирования.
- •
В первую очередь направлено на архитектурную реконструкцию и визуализацию.
- •
Объемные модели содержат информацию, отсутствующую в методах сетки / поверхности.
- •
Позволяет гибкое параметрическое моделирование.
Abstract
В этой статье описывается объемный подход к процедурному моделированию форм и новый язык процедурного моделирования форм (PSML), который упрощает спецификацию этих моделей.PSML предоставляет программистам возможность описывать формы в терминах их трехмерных элементов, где каждый элемент может быть семантической группой трехмерных объектов, например кирпичной стеной, или неделимым объектом, например отдельным кирпичом. Такое моделирование форм облегчает создание моделей, которые более точно соответствуют организации и структуре своих реальных аналогов. Таким образом, пользователи могут запрашивать у этих моделей объемную информацию, такую как количество, положение, ориентация и объем трехмерных элементов, которые не могут быть предоставлены с использованием методов построения моделей на основе поверхности.PSML также предоставляет ряд новых специфичных для языка возможностей, которые позволяют реализовать широкий спектр контекстно-зависимого поведения и функций пост-обработки. Эти возможности включают объектно-ориентированный подход к проектированию модели, методы запроса модели для получения информации на основе компонентов и возможность доступа к элементам и компонентам модели для выполнения логических операций с частями модели. PSML является открытым исходным кодом и включает в себя бесплатные обучающие видеоролики, демонстрационный код и интегрированную среду разработки для поддержки написания программ PSML.
Ключевые слова
Язык моделирования
Процедурные модели
Грамматика формы
Представление формы
Объемное моделирование
Рекомендуемые статьиЦитирующие статьи (0)
© 2021 Авторы. Опубликовано Elsevier Ltd.
Рекомендуемые статьи
Цитирование статей
Произошла ошибка при настройке вашего пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Схема работы светодиодной матрицы объемного дисплея, отображающего несколько полноцветных динамических изображений
1.
Введение
Объемные дисплеи визуализируют трехмерные (3-D) изображения в пространстве реального объема. 1 — 4 Зрители могут наблюдать трехмерные изображения с любой окружающей точки обзора, не требуя дополнительных устройств. Следовательно, объемные дисплеи могут применяться для трехмерной визуализации во многих областях.
Ранее мы предложили алгоритм, который использует трехмерную архитектуру объемных дисплеев для разработки системы отображения информации, демонстрирующей несколько двумерных (2-D) изображений в разных направлениях с характеристиками направленности. 5 — 8 Как показано на рис. 1 (a), зрители могут просматривать различные изображения в зависимости от точек обзора объемного дисплея, разработанного алгоритмом. Возможные варианты использования системы включают цифровые вывески, системы безопасности, искусство и развлечения, поскольку она может предоставлять разную двумерную информацию нескольким людям одновременно.
Рис. 1
Трехмерная структура, показывающая несколько изображений: (а) стеклянный куб, показывающий три изображения. (б) Объемный дисплей на основе светодиодов, показывающий два многоцветных динамических изображения: алфавит на виде спереди и цифры на виде сбоку.
Объемный дисплей, показанный на рис. 1 (а), был сделан с помощью стеклянного куба, в котором много мелких трещин было вызвано лазером. На дисплее представлены три монохроматических статических изображения. Более того, в более раннем исследовании, 5 , мы представили краткое введение в объемный дисплей, состоящий из 8 × 8 × 8 светодиодов (светодиодов) как применение предложенного алгоритма, и показали схему системы, демонстрирующей динамические характеристики. цветные изображения (алфавит и цифры) в двух направлениях, как показано на рис.1 (б). В этой статье мы более подробно опишем аппаратную часть системы объемного отображения.
Однако только восемь цветов (красный, зеленый, синий, голубой, пурпурный, желтый, белый и черный) доступны в вышеупомянутой системе, которая использует микрокомпьютер для управления световой схемой трехмерной светодиодной матрицы. Поэтому, помимо описания многоцветной системы, мы стремимся достичь полноцветного представления, управляя цветом излучения каждого элемента объема (вокселя) светодиодной матрицы.Для полноцветного изображения использовалась широтно-импульсная модуляция (ШИМ). 9 , 10 В ШИМ градация интенсивности света представлена простым управлением соотношением включения / выключения светодиодов за короткий период. То есть регулировка времени свечения красных, зеленых и синих светодиодов обеспечивает полноцветное представление. Обратите внимание, что для достижения ШИМ необходима высокоскоростная обработка сигнала. Поэтому мы спроектировали и разработали специальную схему управления светодиодной матрицей с использованием программируемой вентильной матрицы (FPGA), которая работает на более высокой частоте и больше подходит для параллельных вычислений, чем микрокомпьютеры.
Кроме того, мы проверяем работу системы и демонстрируем, что она показывает разные полноцветные динамические изображения в двух ортогональных направлениях. Эта система представляет собой прототип направленного отображения на основе предложенного нами ранее алгоритма 5 — 8 , который позволяет нескольким зрителям получать двухмерные изображения независимо и одновременно.
2.
Аппаратное обеспечение
В этом разделе мы описываем аппаратное обеспечение предлагаемых систем: многоцветный объемный дисплей и полноцветный объемный дисплей.
2.1.
Многоцветная система объемного дисплея
Светодиодный объемный дисплей состоит из двух блоков: блока отображения и блока управления. Светодиодная матрица, используемая в качестве блока отображения, состоит из восьми светодиодных плат, на которых установлены полноцветные светодиоды 8 × 8, как показано на рис. 2 (а). Эти платы были получены путем разборки коммерчески доступного продукта (3-D LED Cube MB8X, LEDGEND Technology Inc.). На каждой из плат по 12 драйверов светодиодов с последовательным входом / параллельным выходом (SCT2024 11 ), каждый из которых имеет 16 параллельных выходов, подключены каскадом, как показано на рис.2 (б). Для каждой светодиодной платы 192 элемента (Els) (64 вокселя × 3 канала) могут управляться независимо, используя только один последовательный вход. Каналы 1, 2 и 3 представляют красный (R), зеленый (G) и синий (B) соответственно. Здесь максимальная частота светодиодных драйверов составляет 25 МГц.
Рис. 2
Дисплейный блок. (а) Принципиальная схема светодиодных плат. Объемный дисплей состоит из восьми светодиодных табло. (b) Упрощенная блок-схема светодиодных плат, состоящая из драйверов светодиодов с последовательным входом / параллельным выходом.
Эти драйверы светодиодов управляются четырьмя однобитными сигналами: тактовым сигналом (CLK), последовательным вводом данных (SDI), защелкой (LA /) и разрешением вывода (OE /) в следующих шагах. Во-первых, данные фиксируются, когда LA / низкий. LA / должен быть низким, пока данные SDI вводятся в драйверы. Затем данные SDI вводятся последовательно из красного канала воксела 1 в синий канал воксела 64 через регистры сдвига, как показано на фиг. 2 (а) и 2 (б). SDI дискретизируется по переднему фронту CLK. Когда LA / переводится в высокий уровень после ввода данных SDI, данные в регистре сдвига проходят.Когда для OE / установлено низкое значение, выходы драйверов светодиодов включаются, и некоторые светодиоды включаются в соответствии с входным SDI. Таким образом, произвольные шаблоны освещения могут быть представлены только четырьмя однобитными сигналами на одну светодиодную плату, а именно SDI, CLK, LA / и OE /. Мы подробно объясним, как управлять четырьмя сигналами, на конкретном примере ниже (показанном на рисунке 3).
Рис. 3
Конкретный пример временной диаграммы обработки в системе многоцветного объемного отображения.
В качестве блока управления мы использовали плату микрокомпьютера Arduino Mega 2560 (Arduino, LLC), которая имеет 54 цифровых контакта ввода / вывода и может легко управляться языком программирования Arduino на основе C / C ++. Микрокомпьютер генерирует управляющие сигналы в соответствии с исходным кодом, записанным во флэш-ПЗУ платы, и отправляет их на дисплей для визуализации трехмерных изображений. Рабочая частота микрокомпьютера 16 МГц.
На рисунке 3 показан конкретный пример временной диаграммы обработки.Сначала мы описываем четыре управляющих сигнала для платы светодиодов. На временной диаграмме Els 1, 2 и 3 соответствуют каналам R, G и B воксела 1 соответственно, как описано на фиг. 2 (b). Когда OE / высокий, все светодиоды на плате не светятся. Когда OE / устанавливается на низкий уровень, некоторые светодиоды излучают свет в соответствии с сигналами SDI; таким образом, все воксели платы имеют соответствующие цвета (красный, зеленый, синий, голубой, пурпурный, желтый, белый или черный). Мы называем продолжительность светового излучения периодом отображения.SDI высокий только тогда, когда он соответствует El 1; таким образом, воксел 1 становится красным во время периода отображения. Точно так же воксели 2, 3 и 64 становятся зелеными, пурпурными (красный + синий) и белыми (красный + зеленый + синий) соответственно. Управлять всеми восемью платами одновременно с одного микрокомпьютера сложно, потому что он не подходит для параллельной обработки. Таким образом, микрокомпьютер последовательно управляет восемью платами.
2.2.
Система полноцветного объемного дисплея
В многоцветной системе, которая является первым прототипом светодиодного объемного дисплея, мы использовали плату микрокомпьютера в качестве блока управления и смогли продемонстрировать, что блок отображения работает должным образом.Однако дисплейный блок может отображать только состояния включения / выключения (1 бит) для каждого цветового канала из-за структурной структуры светодиодной матрицы, как описано в разд. 2.1. Для представления полноцветных трехмерных изображений требуется блок управления, реализующий ШИМ. Производительность блока индикации зависит от максимальной рабочей частоты драйвера светодиода (25 МГц) и достаточна для ШИМ. Однако микрокомпьютер не подходит для ШИМ из-за его ограниченной максимальной рабочей частоты (16 МГц) и свойств обработки (последовательная обработка).Поэтому мы разработали блок управления с ПЛИС для получения полноцветного трехмерного изображения с ШИМ, как показано на рис. 4.
Рис. 4
Объемный дисплей на основе светодиодов, который может отображать полноцветные динамические 3- D изображения.
Главный ПК отправляет воксельные данные трехмерного изображения на блок управления через интерфейс последовательной связи. Воксельные данные представляют собой информацию о цвете, состоящую из красного, зеленого и синего компонентов, каждая из которых имеет 8-битную глубину. Блок управления генерирует управляющие сигналы из данных вокселя с помощью ШИМ и отправляет их на блок дисплея.Блок отображения отображает произвольные трехмерные изображения на основе полученных управляющих сигналов. Мы разработали программное обеспечение для управления главным компьютером с помощью Visual Studio 2015 как приложения Windows Forms.
Блок управления реализован на плате Atlys (Digilent Inc.) 12 , на которой установлена микросхема ПЛИС Spartan-6 LX45 13 , работающая на частоте 100 МГц. Блок управления управляет дисплеем с помощью цифровых контактов ввода / вывода, которые активируются дополнительной макетной платой (VmodBB, Digilent Inc.) прикреплен к доске Atlys.
На рисунке 5 показана блок-схема блока управления. Каждый блок подробно описывается следующим образом:
1. Блок контроллера последовательного порта получает воксельные данные от главного ПК через последовательный порт, установленный на плате Atlys. 1-битные последовательные данные хранятся в памяти и отправляются в блок гамма-коррекции 8-бит × 8-бит. Общее количество данных, необходимых для отображения кадра, составляет 12 288 бит (= 8 бит × 3 канала × 512 вокселей). Скорость последовательной связи гибкая и может быть увеличена до 12 Мбит / с. 14 В этой системе мы установили скорость передачи данных 1,8 Мбит / с. Эта скорость связи достаточно высока для реализации системы отображения в реальном времени (например, системы с частотой обновления 60 Гц).
2. Как правило, выходная мощность (интенсивность света) обычного двухмерного дисплея пропорциональна γ ’степени входного сигнала, при этом γ регулируется таким образом, чтобы градация цвета казалась естественной для человеческого глаза. Здесь γ называется значением гаммы и обычно принимает значения от 1,8 до 3,0. Блок гамма-коррекции в нашей схеме повышает вход до 2.2-я степень. Входом этого блока является 8-битный сигнал, который представляет значение градации канала (красный, зеленый или синий). Блок был разработан с 9-битным выходом. Битовая длина вывода на 1 бит больше, чем длина ввода, чтобы предотвратить потерю информации. Процесс реализован в виде справочной таблицы с 8-битным входом / 9-битным выходом. Здесь каждый вход и выход этого блока — это число согнутой точки.
3. Значения градации с гамма-коррекцией сохраняются в RAM в блоке PWM.Здесь требуется восемь ОЗУ для параллельного управления восемью платами светодиодов. Блок PWM создает 1-битный сигнал (SDI) из 9-битных значений градации в соответствии с принципом PWM и отправляет SDI в ответ на запрос от блока контроллера дисплея. Блок PWM отправляет восемь сигналов SDI в блок контроллера дисплея.
4. Блок контроллера дисплея запрашивает данные SDI от блока PWM в нужный момент и выводит три сигнала (CLK, LA / и OE /) в дополнение к принятым данным SDI.Здесь частота CLK составляет 25 МГц, что составляет 1/4 рабочей CLK платы Atlys, поскольку драйверы светодиодов работают на максимальной частоте 25 МГц. Ширина импульса (длительность OE /) устанавливается равной времени отправки 192 данных SDI (7,68 мкс). Для параллельного управления восемью платами светодиодов требуется четыре управляющих сигнала (CLK, SDI, LA / и OE /) для каждой платы светодиодов.
Рис. 5
Блок-схема блока управления, реализованного на плате Atlys.
Используя конкретный пример, показанный на рис. 6 (a), процесс обработки описывается следующим образом. Мы рассматриваем случай, когда каналы RGB воксела 1 с гамма-коррекцией равны 511, 255 и 127 соответственно. Последовательность процессов, которые подробно описаны в описании многоцветной системы, необходимо повторить 511 раз для отображения кадра полноцветного трехмерного изображения. В блоке PWM был реализован 9-битный счетчик (CNT), увеличиваемый с интервалами ширины импульса. Путем включения соответствующих светодиодов только тогда, когда 9-битные входные данные вокселей выше, чем CNT, может быть достигнута желаемая яркость, пропорциональная входным данным вокселей.
Рис. 6
Конкретный пример потока обработки. (а) Описание полноцветного представления с использованием ШИМ и (б) временная диаграмма обработки.
На рисунке 6 (b) показана временная диаграмма. В случае, показанном на рис. 6 (a), когда CNT находится в диапазоне от 1 до 127, все каналы (RGB) воксела 1 должны включиться, пока OE / находится на низком уровне. Когда CNT находится между 128 и 255, каналы R и G воксела 1 должны включаться, а канал B — нет. Когда CNT находится между 256 и 511, должен включаться только канал R воксела 1.При этом светодиод вокселя 1 излучает свет желаемого цвета (в данном случае оранжевого).
3.
Алгоритм проектирования
В этом разделе описывается алгоритм 5 , используемый для определения шаблона свечения для светодиодной матрицы, демонстрирующей несколько изображений. Здесь мы описываем алгоритм в случае, когда массив показывает два изображения в ортогональных направлениях, как показано на рис. 7. Объемный дисплей содержит P × Q × R объемных Els (вокселов), которые соответствуют 8 × 8 × 8 полных -цветные светодиоды в данном исследовании.Значение вокселя Vijk указывает яркость светодиода в точках (i, j, k) и может быть определено следующим образом:
1. Каждое из исходных изображений настраивается в том направлении, в котором оно требуется для экспонирования. .
2. Перпендикулярные линии (синие линии на рис. 7) проводятся от вокселя к изображениям A и B.
3. Vijk вычисляется, как показано в уравнении. (1), где aij и bkj соответствуют значениям пикселей исходных изображений A и B на пересечениях с каждой перпендикулярной линией
Теперь мы рассмотрим изображения, представленные объемным дисплеем, с определенными вокселями.Мы предполагаем, что значения пикселей представленных изображений задаются суммированием значений вокселей вдоль направлений проекции, когда мы смотрим на дисплей с расстояния. Следовательно, aij ‘и bij’, значения пикселей выставленных изображений A и B, представлены, как показано в уравнениях. (2) и (3), соответственно
Ур. (2)
aij ′ = ∑k = 1RVijk = aij (b1j + b2j +… + bRj),Ур. (3)
bkj ′ = ∑i = 1PVijk = bkj (a1j + a2j +… + aRj).Обратите внимание, что представленные изображения получены путем умножения исходного изображения и фонового шума, соответствующего помехам от другого изображения.Исходные компоненты изображения в уравнениях. (2) и (3) имеют тенденцию преобладать над фоновым шумом; таким образом, выставленные изображения распознаются как исходные изображения. 5 С другой стороны, это распознавание происходит только тогда, когда мы смотрим на объемный дисплей с соответствующей точки зрения, то есть выставленные изображения имеют характеристики направленности.
Рис. 7
Алгоритм работы светодиодной схемы освещения.
Применяя описанную выше процедуру расчета к каждому каналу, можно создать объемный дисплей, показывающий два полноцветных изображения.О возможности полноцветного расширения алгоритма сообщалось в предыдущей работе с использованием технологии струйной печати. 15 Это исследование экспериментально продемонстрировало, что алгоритм может быть применен к случаю, когда в качестве оригиналов использовались сложные изображения (например, полноцветные фотографии).
4.
Результаты
4.1.
Оценка излучения света
Чтобы оценить систему полноцветного объемного дисплея, мы измерили яркость вокселя (Y) на входе (X) с главного ПК с помощью измерителя мощности лазера (LP1, Sanwa Electric Instrument Co ., Ltd.), как показано на рис. 8 (а). Стабилизированный источник питания постоянного тока подавал на дисплей постоянное напряжение 4,0 В. Синий график на рис. 8 (b) показывает нормированную яркость, когда цвет вокселя красный. Результат соответствует теоретическому значению нормализованного Y = X2.2, где X — цифровое значение, отправленное с главного ПК на блок управления, а Y — нормализованное значение яркости. Среднеквадратичная ошибка между экспериментальным результатом и теоретическим значением практически равна нулю (1 × 10-3).Мы получили практически идентичные результаты для других цветов вокселей (зеленого и синего). По этим результатам мы проверили выход разработанной системы.
Рис. 8
Измерение яркости воксела: (а) экспериментальная установка и (б) измеренная яркость воксела. X — это цифровое значение, отправленное с главного ПК на блок управления, а Y — это нормализованное значение яркости.
4.2.
Объемный дисплей, показывающий два полноцветных динамических шаблона
На рисунке 9 показан объемный дисплей, демонстрирующий различные полноцветные динамические изображения в двух ортогональных направлениях.Как показано на фиг. 9 (a) и 9 (c), одно изображение представляет собой строку алфавита (от A до L), наблюдаемую спереди дисплея, а другое — последовательность чисел (от 0 до 9), наблюдаемую сбоку. Различные изображения наблюдаются с разных точек зрения, как показано на рис. 9 (б) и 9 (г). См. Также видео 1. Когда объемный дисплей наблюдался с точек зрения, отличных от вида спереди и сбоку, никаких значимых изображений получить не удалось. В частности, зоны просмотра выставленных изображений были узкими. Это показывает, что разработанная система имеет характеристики направленности.
Рис. 9
Объемный дисплей с двумя полноцветными динамическими узорами (см. Видео 1). (a) Исходные изображения вида спереди (от A до L), (b) проецируемые образцы вида спереди, (c) исходные изображения вида сбоку (от 0 до 9) и (d) проецируемые образцы вида сбоку (MPEG, 1,7 МБ [URL: http://dx.doi.org/10.1117/1.OE.56.7.073108.1]).
Чтобы продемонстрировать полноцветное представление системы, каждому кадру было присвоено значение оттенка на 5 градусов больше, чем у предыдущего кадра, как показано на рис.9, на котором отображается 1/3 всех кадров. Здесь мы устанавливаем максимальные значения насыщенности и яркости изображений. Цветовые координаты оттенок – насыщенность – яркость преобразуются в значения красный – зеленый – синий (RGB) перед передачей в систему, поскольку разработанная система основана на цветовой модели RGB. На рис. 9 оттенок изображения увеличивается слева направо: H = 15 градусов, 30 градусов, 45 градусов,…, 360 градусов. Многоцветная система объемного отображения может отображать только восемь цветов, тогда как разработанная система может отображать цвета, которые не могут быть представлены многоцветной системой, например оранжевый и фиолетовый.
5.
Обсуждение
Сначала обсудим изображение, которое демонстрирует развернутый объемный дисплей. На изображениях, представленных на рис. 9 (b) и 9 (d), яркость различается в зависимости от расположения пикселей. Это различие было вызвано помехами от другого изображения, как описано в разд. 3. Мы считаем, что такие перекрестные помехи можно уменьшить с помощью итерационного метода, предложенного в предыдущем исследовании. 8 Кроме того, разработанная система, имеющая 8 × 8 × 8 вокселей, меньше по масштабу, чем стеклянный прототип, показанный на рис.1 (а), который имеет 64 × 64 × 64 вокселей. Таким образом, разработанная система могла отображать только простые изображения, например, персонажа. В будущей работе мы разработаем большую систему для показа сложных изображений, таких как фотографии. Более того, мы обнаружили проблему в системе, заключающуюся в том, что некоторые воксели скрыты передней черной печатной платой. Прозрачная печатная плата решит эту проблему.
Далее мы обсудим частоту кадров дисплея. Количество Els на светодиодной плате — 192 (64 вокселя × 3 канала).Следовательно, блоку управления требуется 7,68 мкс для отправки 192 данных SDI на дисплей с CLK 25 МГц (192/25 МГц = 7,68 мкс). Как упоминалось в п. 2.2 ширина импульса (длительность OE /) устанавливается равной времени, равному времени отправки данных SDI (7,68 мкс). Таким образом, всего для представления кадра требуется 7,85 мс, поскольку цикл отправки данных и разрешения вывода повторяется 511 раз (2 × 7,68 мкс × 511 = 7,85 мс). Когда скорость последовательной связи составляет 1,8 Мбит / с, общее время связи между главным ПК и блоком управления для всех воксельных данных кадра составляет ~ 6.83 мс (= 8 бит × 3 канала × 512 вокселей / 1,8 Мбит / с). Поскольку время связи на кадр короче, чем время вычисления, связь между главным ПК и блоком управления может быть завершена, представляя предыдущий кадр. Следовательно, время связи не нужно учитывать для определения частоты кадров дисплея. В результате частота кадров разработанной системы определяется только временем расчета и составляет ∼127 Гц (= 1 / 7,85 мс). Здесь мы обсуждаем ограничение количества вокселей на основе частоты кадров обычного телевидения (30 Гц).Если дисплей работает с частотой 30 Гц, блок управления, разработанный в этом исследовании, может контролировать в четыре раза больше вокселов, чем в существующей системе (127 / 30≈4), например, 16 × 16 вокселей на четыре управляющих сигнала.
Наконец, обсудим спроектированную схему управления. В этом исследовании нам удалось разработать простую и легкую в проектировании схему полноцветного объемного дисплея в качестве первого прототипа. Настоящая схема не может реализовать систему отображения в реальном времени, когда количество вокселей увеличивается (более 16 × 16 вокселей на четыре управляющих сигнала).Эта проблема более заметна в области объемных дисплеев, чем в области обычных 2-D дисплеев, потому что количество вокселов увеличивается в кубическом порядке. Мы разработаем систему с более высоким разрешением за счет увеличения количества управляющих сигналов и реализации параллельной обработки. С этой целью мы спроектируем и разработаем схему светодиодной матрицы, которой можно будет управлять с помощью более эффективной схемы работы. Например, использование полноцветных светодиодов, содержащих управляющие микросхемы, кажется хорошим подходом для реализации эффективной схемы работы.
6.
Заключение
В этом исследовании мы разработали многоцветную систему объемного отображения в качестве первого прототипа. Кроме того, мы спроектировали и разработали схему управления светодиодной матрицей для реализации полноцветного динамического объемного дисплея. Разработанная схема управления, реализованная на ПЛИС, способна управлять диаграммой свечения светодиодной матрицы параллельно и с высокой скоростью. Таким образом, мы добились представления полноцветных динамических изображений с простой схемной структурой.Кроме того, мы экспериментально оценили систему, измерив яркость воксела с переменным входным сигналом, и нам удалось продемонстрировать, что объемный дисплей демонстрирует два полноцветных динамических изображения. Эта демонстрация показывает будущую расширяемость алгоритма, предложенного в предыдущем исследовании. 5
Благодарности
Эта работа была частично поддержана Японским обществом содействия науке, гранты №№ 16J30007 и 25240015. Авторы заявляют об отсутствии конкурирующих финансовых интересов.
Ссылки
7.
R. Hirayama et al., « Трехмерный кристалл, показывающий несколько двумерных изображений с направленностью ,» (2015). Google ученый9.
П. Нарра и Д. С. Зингер, « Эффективный подход к затемнению светодиодов ,» in Industry Applications Conf., 2004. 39-е Ежегодное собрание IAS, Conf. Запись 2004 IEEE, 1671 –1676 (2004). Google ученыйБиография
Рюдзи Хираяма — научный сотрудник Университета Тиба.Он получил степени бакалавра, магистра и доктора технических наук в Университете Чиба в 2012, 2014 и 2017 годах соответственно. Его текущие исследовательские интересы включают трехмерные (3-D) дисплеи и системы взаимодействия человека с компьютером. Он является членом Оптического общества (OSA), Ассоциации вычислительной техники (ACM) и Японского общества прикладной физики (JSAP).
Ацуши Шираки — доцент. Он получил докторскую степень в Университете Чиба, Япония, в 2008 году. Его исследовательские интересы — трехмерные дисплеи и образовательные технологии.Он является членом Общества обработки информации Японии (IPSJ), Института инженеров электроники, информации и связи (IEICE), Института инженеров по изображениям и телевидению (ITE) и Японского общества образовательных технологий.
Хиротака Накаяма получил докторскую степень в Университете Тиба, Чиба, Япония, в 2011 году. Он работал в Центре вычислительной астрофизики Национальной астрономической обсерватории Японии. Его исследовательские интересы включают технологии компьютерной графики и трехмерные приложения.
Такаши Какуэ — доцент. Он получил докторскую степень в Технологическом институте Киото, Япония, в 2012 году. Его исследовательские интересы — голография, цифровая голография, компьютерная голография, голографическая интерферометрия, трехмерное изображение, высокоскоростная визуализация и сверхбыстрая оптика. Он является членом SPIE, OSA, IEEE, ITE, JSAP, Оптического общества Японии (OSJ), IPSJ и Лазерного общества Японии.
Томоёси Симобаба получил докторскую степень в Университете Чиба в 2002 году и сейчас является доцентом.Его научные интересы — компьютерная голография и ее приложения. Он является членом SPIE, OSA, OSJ, ITE и IEICE.
Томоёси Ито — профессор. Он получил докторскую степень в Токийском университете, Япония, в 1994 году. Его исследовательские интересы — высокопроизводительные вычисления и их приложения, такие как электронная голография для трехмерного телевидения. Он является членом ACM, OSA, ITE, IEICE, IPSJ и Астрономического общества Японии.
Терапия с объемной модулированной дугой с двойным вентилем | Радиационная онкология
Mah D, Hanley J, Rosenzweig KE, Yorke E, Braban L, Ling CC, Leibel SA, Mageras G: Технические аспекты техники задержки дыхания на глубоком вдохе при лечении рака грудной клетки. Int J Radiat Oncol Biol Phys 2000, 48: 1175-1185. 10.1016 / S0360-3016 (00) 00747-1
Артикул CAS PubMed Google ученый
Ланген К.М., Джонс Д.Т.: Движение органа и управление им. Int J Radiat Oncol Biol Phys 2001, 50: 265-278. 10.1016 / S0360-3016 (01) 01453-5
Артикул CAS PubMed Google ученый
Xing L, Thorndyke B, Schreibmann E, Yang Y, Li TF, Kim GY, Luxton G, Koong A: Обзор лучевой терапии под визуальным контролем. Мед Досим 2006, 31: 91-112. 10.1016 / j.meddos.2005.12.004
Статья PubMed Google ученый
Сирато Х, Онимару Р., Исикава М., Канеко Дж., Такешима Т., Мочизуки К., Симидзу С., Умегаки К.: 4-мерная лучевая терапия рака легких в режиме реального времени. Cancer Sci 2012, 103: 1-6. 10.1111 / j.1349-7006.2011.02114.x
Артикул CAS PubMed Google ученый
Sharp GC, Jiang SB, Shimizu S, Shirato H: Прогнозирование движения опухоли в дыхательных путях для лучевой терапии в режиме реального времени. Phys Med Biol 2004, 49: 425-440. 10.1088 / 0031-9155 / 49/3/006
Артикул PubMed Google ученый
Кубо HD, Лен П.М., Минохара С., Мостафави Н: Программа лучевой терапии с синхронизацией дыхания в Онкологическом центре Дэвиса Калифорнийского университета. Med Phys 2000, 27: 346-353. 10.1118 / 1.598837
Артикул CAS PubMed Google ученый
Pepin EW, Wu H, Shirato H: Динамическое окно стробирования для компенсации смещения базовой линии при респираторно-управляемой лучевой терапии. Med Phys 2011, 38: 1912-1918. 10.1118 / 1.3556588
PubMed Central Статья PubMed Google ученый
Михайлов И.Б., Фатыга М., Морос Э.Г., Пенагарикано Дж., Лерма Ф.А.: Доза в легких при минимально подвижных поражениях грудной клетки, леченных с помощью респираторного стробирования. Int J Radiat Oncol Biol Phys 2010, 77: 285-291. 10.1016 / j.ijrobp.2009.08.021
Статья PubMed Google ученый
Бербеко Р.И., Нисиока С., Ширато Х., Цзян С.Б.: Остаточное движение опухолей легких при дыхательной закрытой радиотерапии в конце вдоха на основе внешних суррогатов. Med Phys 2006, 33: 4149-4156. 10.1118 / 1.2358197
Артикул PubMed Google ученый
Wu J, Li H, Shekhar R, Suntharalingam M, D’Souza W: Оценка методов планирования стереотаксической лучевой терапии при опухолях легких. Радиатор Oncol 2008, 87: 35-43. 10.1016 / j.radonc.2008.02.010
PubMed Central Статья PubMed Google ученый
Винк Н.М., Чао М., Энтони Дж., Син L: Индивидуализированные окна стробирования, основанные на четырехмерной КТ-информации для респираторно-управляемой лучевой терапии. Phys Med Biol 2008, 53: 165-175. 10.1088 / 0031-9155 / 53/1/011
Артикул PubMed Google ученый
Otto K: Объемно-модулированная дуговая терапия: IMRT в одной гентри-дуге. Med Phys 2008, 35: 310-317. 10.1118 / 1.2818738
Артикул PubMed Google ученый
Crooks SM, Wu X, Takita C, Matzich M, Xing L: Апертурно-модулированная дуговая терапия. Phys Med Biol 2003, 48: 1333-1344. 10.1088 / 0031-9155 / 48/10/307
Артикул CAS PubMed Google ученый
Yu CX: Дуговая терапия с модуляцией интенсивности и динамической многолепестковой коллимацией: альтернатива томотерапии. Phys Med Biol 1995, 40: 1435-1449. 10.1088 / 0031-9155 / 40/9/004
Артикул CAS PubMed Google ученый
Фокс Т., Саймон Э.Л., старейшина Э., Риффенбург Р.Х., Джонстон, штат Пенсильвания: Закрытая доставка со свободным дыханием (FBGD) лучевой терапии легких: анализ факторов, влияющих на пропускную способность клинических пациентов. Рак легких 2007, 56: 69-75. 10.1016 / j.lungcan.2006.11.019
Статья PubMed Google ученый
Мерфи М.Дж., Лин П.С., Ожасоглу C: Время введения внутрифракционной дозы во время стереотаксической лучевой терапии может влиять на радиобиологический эффект. Med Phys 2007, 34: 481-484. 10.1118 / 1.2409750
Артикул CAS PubMed Google ученый
Chin E, Otto K: Исследование нового алгоритма для истинного планирования 4D-VMAT в сравнении с отслеживаемой, закрытой и статической доставкой. Med Phys 2011, 38: 2698-2707. 10.1118 / 1.3578608
Артикул PubMed Google ученый
Geneser S, Kirby N, Xing L, Pouliot J ASTRO Proceedings. Влияние ошибок в нежестких методах регистрации медицинских изображений на точность искажения дозы 2012.
Google ученый
Geneser S, Fahimian B, Xing L: Повышение эффективности закрытых родов с помощью коротких задержек дыхания на вдохе и выдохе. Med Phys 2013, 40: 296.
Статья Google ученый
Suh Y, Sawant A, Venkat R, Keall PJ: Четырехмерное планирование лечения IMRT с использованием алгоритма отслеживания движения DMLC. Phys Med Biol 2009, 54: 3821-3835. 10.1088 / 0031-9155 / 54/12/014
Артикул PubMed Google ученый
Трофимов А., Рицель Э., Лу Х.М., Мартин Б., Цзян С., Чен Г.Т., Бортфельд Т: Темпоро-пространственная оптимизация IMRT: концепции, реализация и начальные результаты. Phys Med Biol 2005, 50: 2779-2798. 10.1088 / 0031-9155 / 50/12/004
Артикул PubMed Google ученый
Suh Y, Weiss E, Zhong H, Fatyga M, Siebers JV, Keall PJ: Поставляемый четырехмерный метод планирования лучевой терапии с модуляцией интенсивности для динамической доставки слежения за опухолью с помощью многолепесткового коллиматора. Int J Radiat Oncol Biol Phys 2008, 71: 1526-1536.10.1016 / j.ijrobp.2008.04.018
PubMed Central Статья PubMed Google ученый
Gong G, Wang R, Guo Y, Zhai D, Liu T, Lu J, Chen J, Liu C, Yin Y: Сниженная доза легких во время лучевой терапии рака грудного отдела пищевода: VMAT в сочетании с активным контролем дыхания для умеренного ДИБХ. Radiat Oncol 2013, 8: 291. 10.1186 / 1748-717X-8-291
PubMed Central Статья PubMed Google ученый
Thomas E, Popple RA, Prendergast BM, Clark GM, Dobelbower MC, Fiveash JB: Влияние сглаживающей безфильтровой и волюметрической дуговой терапии на эффективность лечения. J Appl Clin Med Phys 2013, 14: 6.
Google ученый
Сжатие объемных изображений в формате JPEG2000
Медицинское и научное оборудование для визуализации генерирует значительный объем объемных данных. Поскольку такие наборы данных имеют тенденцию быть очень большими, мощная технология сжатия имеет решающее значение для эффективного хранения и передачи, произвольного доступа, поддержки области интереса (ROI) и масштабируемости разрешения / качества.
JPEG2000, текущий стандарт, разработанный Joint Photographic Expert Group (JPEG), обеспечивает эту функциональность для наборов 2D-данных посредством Части 1 (Базовые системы кодирования) 1 и Части 2 (Расширения). 2 Хотя последний косвенно поддерживает трехмерное вейвлет-преобразование посредством расширенного многокомпонентного преобразования, полная схема объемного кодирования по-прежнему важна для функциональности, оптимальных характеристик скорости-искажения и изотропного поведения для всех измерений.
Сжатие объемных изображений с помощью JP3D
Часть 10 JPEG2000 3 (JP3D), которая касается объемного изображения, направлена на обеспечение той же функциональности и эффективности для наборов 3D-данных, что и для его 2D-аналогов. Спецификация JP3D в настоящее время находится на стадии окончательного раскрытия международного стандарта (FDIS), что означает, что все функции были определены и окончательно доработаны, и ей нужно только пройти процесс голосования. Он разработан как чистое расширение Части 1 и Части 2.Таким образом, JP3D поддерживает существующие возможности Части 1, расширенные до трех измерений. Он также уважает синтаксис и возможности многокомпонентных изображений Части 2, хотя не расширяет их все. Функции, относящиеся к кодированию объемного набора данных, такие как ядра произвольного преобразования (ATK) и кодирование ROI, расширяются, в то время как менее важные функции не принимаются.
Важной целью JP3D является обеспечение максимально изотропной спецификации путем поддержки идентичных возможностей обработки во всех измерениях, даже несмотря на то, что синтаксис кодового потока Части 1 и Части 2 различает две пространственные оси и ось перекрестных компонентов.Очевидно, что типичные функции, такие как масштабируемость качества и разрешения, а также кодирование ROI, также должны поддерживаться JP3D изотропным образом.
Кроме того, синтаксис пакетов JP3D совместим с интерактивными протоколами, определенными в JPIP 4 (часть 9) для взаимодействия клиент-сервер. Этот протокол позволяет приложениям получать произвольный доступ к потокам удаленного кода, таким образом используя все возможности масштабируемости JPEG2000.
Чтобы снизить стоимость реализации и сохранить относительно простой дизайн кодека, спецификации JP3D не вводят новых концепций кодирования, а повторно используют концепцию, определенную в Части 1 и Части 2, то есть встроенное блочное кодирование путем оптимизированного усечения 5 (EBCOT), основанный на принципах многоуровневого нулевого кодирования (LZC), который является основным элементом стандарта сжатия изображений JPEG2000.
Внутри кодека JP3D
Подобно JPEG2000 Часть 1, кодек JP3D сначала разбивает набор объемных данных. Плитки в этом случае являются кубовидными подобъемами, которые затем независимо кодируются. Кроме того, все компоненты кодируются как отдельные наборы данных в градациях серого. Таким образом, кодирование набора данных изображения фактически означает кодирование компонентов мозаичного изображения.
Рисунок 1. Разделение поддиапазонов на кодовые блоки двоичного размера.
Затем дискретное вейвлет-преобразование (DWT) фильтрует все коэффициенты выборки тайлов с использованием шаблона разложения Маллата.Количество уровней декомпозиции в каждом из трех измерений можно свободно выбирать. После этого кодек разделяет результирующие поддиапазоны на небольшие кубы двоичного размера, называемые кодовыми блоками, которые кодер EBCOT затем независимо кодирует (см. Рисунок 1). Коэффициенты трехмерного кодового блока обрабатываются в порядке битовой плоскости на битовую плоскость и среза за срезом, как показано на рисунке 2. Внутри битовой плоскости среза шаблон сканирования идентичен шаблону JPEG2000 Часть 1, в котором биты сканируются группами из четырех вертикально выровненных битов (сканирование на основе полос).Как только битовая плоскость слайса полностью обработана, алгоритм переходит к следующему слайсу в кодовом блоке.
Рисунок 2. Трехмерный шаблон сканирования кодовых блоков.
Рис. 3. График производительности сжатия, показывающий пиковое отношение сигнал / шум в зависимости от полученных битрейтов для компьютерной томографии (КТ) и магнитно-резонансного изображения (МРТ). Работа в процессе
В настоящее время арифметический кодировщик 3D EBCOT-кодера все еще использует 2D-контекстную модель из Части 1.Это можно объяснить тем фактом, что определение общей трехмерной контекстной модели оказывается неожиданно трудным из-за анизотропного поведения большинства объемных наборов данных и высокой степени сложности, связанной с процессом моделирования. Тем не менее, текущая стандартная спецификация JP3D была определена так, что для этой части можно легко указать улучшенные контекстные модели. В этом смысле предыдущие 6 и текущие исследования 7,8 по трехмерному контекстному моделированию и проектированию привели к значительному увеличению — до 10% — производительности сжатия по сравнению с двумерными контекстными моделями, используемыми в Части 1 стандарта.

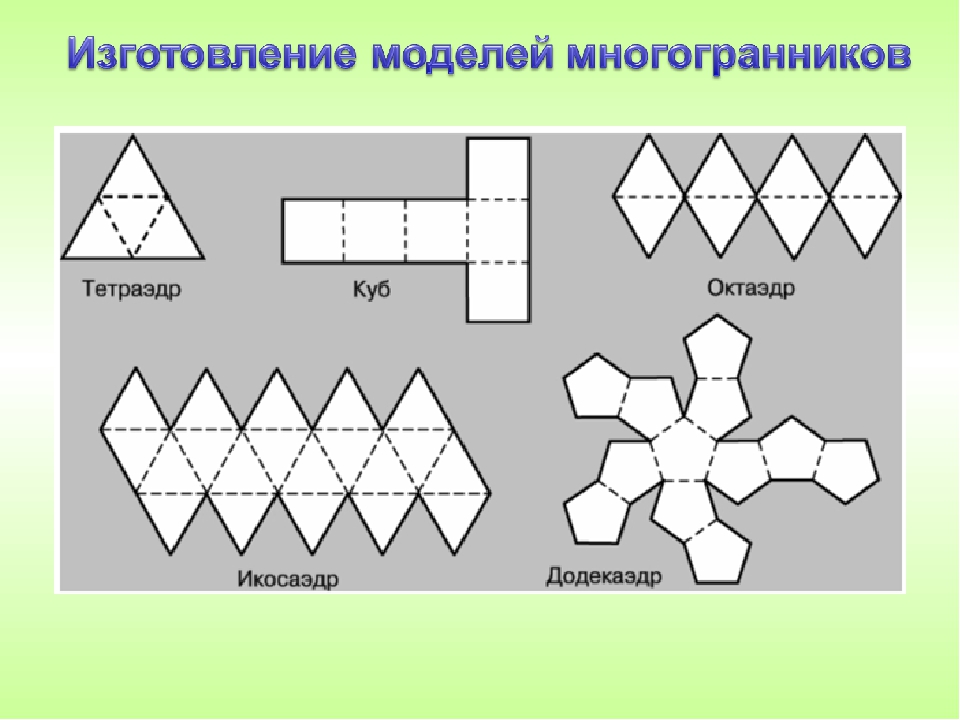 Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом
Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.