Как сделать ромб из бумаги схема: Как сделать ромб из бумаги. Оригами ромб из бумаги — YouTube

Геометрия можно распечатать на кусочек бумаги

Автор Иван Иванов На чтение 19 мин Просмотров 18 Опубликовано 28 февраля, 2023

Здравствуйте, друзья! Как я и обещала в прошлый раз сегодня мы подготовили для детей шаблоны геометрических фигур для вырезания из бумаги. Среди них вы найдете круг, треугольник, квадрат, овал и прямоугольник. В этот раз все геометрические фигуры раскрашены в различные яркие цвета. Если вам нужны они просто белые, бесцветные, то советую посмотреть нашу прошлую статью.

Содержание

1. Геометрические трафареты для вырезания из бумаги распечатать
2. Шаблон для аппликации из геометрических фигур
3. Макеты из бумаги
4. Шаблон геометрических фигур: скачать и распечатать
5. Плоские геометрические фигуры из бумаги – Строим замок
6. Плоские геометрические фигуры из бумаги – Строим замок
7. Как сделать объемные геометрические фигуры из бумаги (схемы, шаблоны)?
8. Геометрические фигуры схемы
9. Как сделать объемные геометрические фигуры
10. Из бумаги
11. Из картона
12. Развертки куба
13. Треугольника
14. Прямоугольника
15. Цилиндра
16. Ромба
17. Схемы для вырезания
18. Конуса
19. Пирамиды
20. Шестигранника
21. Макета с припусками
22. Параллелепипеда
23. Трапеции
24. Овала
25. Многогранника
26. Параллелограмма
27. Шаблоны для склеивания
28. Сложных фигур
29. Октаэдра
30. Тетраэдра
31. Икосаэдра
32. Додекаэдра
33. Гексаэдра
34. Фигурок из треугольников
35. Макеты из бумаги
36. Оригами
37. Животные
38. Корабль
39. Полигональные чертежи
40. Игрушки из фигур
41. Геометрические маски
42. Карандаш
43. Как вырезать и склеить модели из бумаги
44. Как сделать куб из бумаги?
45. Скачать:

Геометрические трафареты для вырезания из бумаги распечатать

Дети хорошо развиваются, если с раннего возраста показывать им цветные геометрические фигуры, как на шаблоне ниже. Достаточно его скачать и можно распечатать на плотной бумаге.

Скачать шаблон можно в формате PDF, который можно распечатать прямо с браузера.

Шаблон для аппликации из геометрических фигур

Отлично учатся геометрические фигуры, если дети занимаются интересной аппликацией из них. Распечатав данный PDF шаблон на А4, и вырезав каждую фигуру, из них можно сложить детский паровозик.

1.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

Мы видим, что вершины и стороны прямого угла совпали, значит, угол прямой, а треугольник прямоугольный.

Макеты из бумаги

Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.

Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.

Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.

Шаблон геометрических фигур: скачать и распечатать

Поделки из фигур доступны для занятий с детьми с самого младшего возраста.

Для малышей 2-4 лет задание не должно включать в себя больше 5 деталей. В противном случае ребенок быстро устает, путается, а внимание его рассеивается. Для изготовления поделки малышу необходимо приготовить готовые элементы поделки из цветной бумаги и предложить основу с готовым контуром. Или показать, последовательность выполнения работы. Дети в возрасте 4-5 лет могут вырезать из бумаги простые детали самостоятельно, но под присмотром взрослых. Для работы ребенку необходимы ножницы с закругленными концами. Дети такого возраста способны сами выполнить поделки средней сложности. Учащиеся младших классов справляются самостоятельно с достаточно сложными заданиями.

Для того, чтобы заинтересовать ребенка изготовлением поделки из геометрических фигур, можно предложить ему интерактивную игру на основе сказки “Мышонок и карандаш”. Затею эту можно осуществить в домашних условиях на занятиях в детском саду. Необходимо заранее приготовить элементы, из которых состоит кошка: круги, овалы и треугольники.

Увлекательная игра поможет сделать творческий процесс интереснее для очень активных детей.

Плоские геометрические фигуры из бумаги – Строим замок

В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).

Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.

После этого подробно объесните ребенку инструкцию к выполнению упражнения.

“Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них”, – взрослый показывает одну или две игровых схемы замка с нашего задания. – “Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.” – взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.

Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.

Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.

Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.

Здесь вы можете скачать объемные геометрические фигуры из бумаги в виде разверток, которые необходимо распечатать на принтере, вырезать и склеить по указанным местам. В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.

Итак, в первом листе мы выложили следующие геометрические фигуры: куб (фигура, поверхность которого состоит из 6 квадратов), трехгранная пирамида (основание пирамиды и 3 грани), четырехгранная пирамида (основание и 4 грани), ромб (фигура, визуально состоящая из двух пирамид, имеющих общее основание). Во втором листе вы найдете развертки таких геометрических фигур из бумаги: шестигранник (фигура, состоящая из шести граней), цилиндр (состоящий из свернутого прямоугольника и двух окружностей-оснований) и конус.

Скачать геометрические фигуры из бумаги – развертки для вырезания вы можете во вложениях внизу страницы

Скачайте и распечатайте 2 листа с фигурами, вырежьте их аккуратно ножницами и склейте в нужных местах. Учтите, что у бумажных фигур есть дополнительные места для сгиба и склеивания (у нас они выделены оранжевым цветом). Все оранжевые места вам необходимо согнуть и намазав их клеем вклеить с внутренней стороны фигуры.

После того, как дети, при помощи взрослых, склеят все геометрические фигуры из бумаги, можно продолжить занятие, задавая детям вопросы. Например: “Покажи мне пирамиду. Сколько у нее сторон? Где ее основание? Чем эта пирамида (показываете трехранную) отличается от этой (четырехранной)? Покажи мне цилиндр. Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?” – и так далее.

В зависимости от возраста ребенка, можно использовать в занятии различные обучающие материалы. Например, что такое пирамида:

Какие бывают пирамиды. (Пусть ребенок покажет из них те, которые он склеил)

Можете также скачать эти обучающие картинки во вложениях.

Плоские геометрические фигуры из бумаги – Строим замок

В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).

Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.

После этого подробно объесните ребенку инструкцию к выполнению упражнения.

“Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них”, – взрослый показывает одну или две игровых схемы замка с нашего задания. – “Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.” – взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.

Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.

Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.

Скачать карточки с плоскими геометрическими фигурами для строительства замка вы можете во вложениях внизу страницы.

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Веселые и красочные задания для детей “Рисунки из геометрических фигур” являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических формю

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.

Задания ознакомят ребенка с основными фигурами геометрии – кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга – это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

Вот здесь можно найти шаблоны более сложных фигур (Платоновы Тела, Архимедовы тела, многогранники, полиэдры, разные виды пирамид и призм, простые и косые бумажные модели).

Как сделать объемные геометрические фигуры из бумаги (схемы, шаблоны)?

Вот несколько схем, по которым можно изготовить объёмные геометрические фигуры.

Чуть сложнее будет изготовить Октаэдр.

А вот эта объёмная фигура – Додекаэдр.

Более подробно об изготовлении объёмных фигур можно посмотреть здесь.

Вот так выглядят объёмные фигуры не в собранном виде:

Из объёмных геометрических фигур можно сделать много оригинальных поделок, в том числе и упаковки для подарка.

Чтобы дети лучше запомнили, какие бывают геометрические фигуры, и знали, как они называются, можно из плотной бумаги или картона сделать Объемные геометрические фигуры. Кстати, на основе их можно изготовить красивую подарочную упаковку.

Самое сложное – это разработать и начертить развёртки, нужны хотя бы базовые знания черчения. Можно взять и готовые развёртки и распечатать на принтере.

Чтобы линия сгиба была ровной и острой, можно воспользоваться тупой иглой и металлической линейкой. При проведении линии иголку нужно сильно нагнуть в направлении движения, практически положив её набок.

Вот здесь можно найти шаблоны более сложных фигур (Платоновы Тела, Архимедовы тела, многогранники, полиэдры, разные виды пирамид и призм, простые и косые бумажные модели).

Кстати, чтобы рассчитать параметры пирамиды, можно воспользоваться вот этой программой.

Прежде чем начать делать объемные геометрические фигуры, нужно представить (или знать как выглядит) фигуру в 3D измерении: сколько граней имеет та или иная фигура.

Сначала необходимо правильно начертить на бумаге фигуру по граням, которые должны быть соединены между собой. У каждой фигуры грани имеют определенную форму: квадрат, треугольник, прямоугольник, ромб, шестиугольник, круг и т. д.

Очень важно, чтобы длина ребер фигуры, которые будут соединены друг с другом имели одинаковую длину, чтобы во время соединения не возникло проблем. Если фигура состоит из одинаковых граней, я бы предложила сделать шаблон во время черчения использовать этот шаблон. Так же можно скачать из интернета готовые шаблоны, распечатать их, согнуть по линиям и соединить (склеить).

Самостоятельно смастерив из бумаги объмные фигуры можно не только использовать их для развлечения, но и для обучения.

Геометрические фигуры схемы

Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.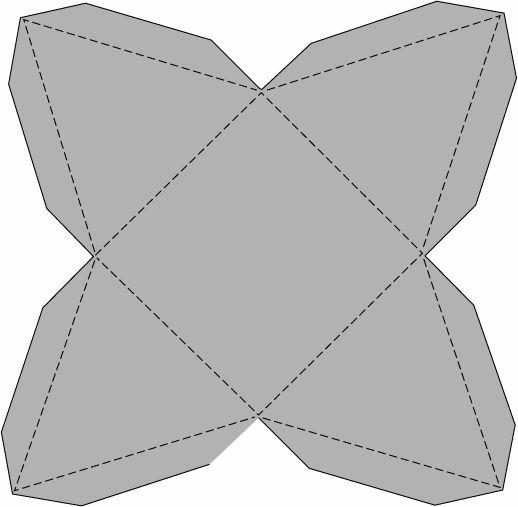

Как сделать объемные геометрические фигуры

Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.

Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.

Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.

Из бумаги

Из картона

Развертки куба

Треугольника

Прямоугольника

Цилиндра

Ромба

Схемы для вырезания

Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.

Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).

Конуса

Пирамиды

Шестигранника

Макета с припусками

Параллелепипеда

Трапеции

Овала

Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.

Материал, из чего можно сделать плотный шар — картон или плотная бумага.

Многогранника

Параллелограмма

Шаблоны для склеивания

Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.

Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.

Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.

Сложных фигур

Октаэдра

Тетраэдра

Икосаэдра

Додекаэдра

Гексаэдра

Фигурок из треугольников

Макеты из бумаги

Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.

Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.

Оригами

Животные

Корабль

Применяется множество вариантов, как сделать кораблик из бумаги.

Полигональные чертежи

Игрушки из фигур

Геометрические маски

Карандаш

Как вырезать и склеить модели из бумаги

Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.

Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.

На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.

Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.

Если Вам понравилась наша статья и Вам есть что добавить, поделитесь своими мыслями. Нам очень важно знать Ваше мнение!

После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!

Как сделать куб из бумаги?

Куб – правильный многогранник, каждая грань которого представляет собой квадрат

Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.

Выбираем размеры квадрата – одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон. Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу. Над и под любыми из квадратов рисуем по одному такому же квадрату. Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской. Куб готов!

После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!

Одним из достоинств этой операции перегибания является то, что ее можно производить, не имея под рукой никаких дополнительных инструментов – ни линейки, ни циркуля, ни даже карандаша. Я выбрала эту тему потому, что сама увлекаюсь рисованием, геометрией и физикой. В своей работе я затрагиваю не только геометрию листа бумаги, но возможность применения листа бумаги для рисования без красок и карандашей, для изучения физических свойств бумаги.

Скачать:

Муниципальный ЭТАП VIII ВСЕРОССИЙСКОГО ДЕТСКОГО КОНКУРСА НАУЧНО-ИССЛЕДОВАТЕЛЬСКИХ И ТВОРЧЕСКИХ РАБОТ «Меня оценят в XXI веке »

Научный руководитель: Веригина Наталья Александровна

Научный руководитель Веригина Наталья Александровна

МОУ Вейделевская СОШ, Белгородская область, п. Вейделевка

Экспериментальные задачи по физике. – М.: «Просвещение», 1974. Необычные учебные материалы по математике. – М.: Школа-Пресс, 2000 Самостоятельная работа учащихся по математике в средней школе. – М.: Просвещение,1981 Родина Л. П. Архимедова сила и киты // Квант. №8. 1982. О. Ф. Кабардин. Физика: Справ. материалы: Учебное пособие для учащихся.-М.: Просвещение, 1991. Книга для чтения по физике 6-7 класс. Составитель И. Г. Кириллова. Внеклассная работа по математике. Автор: И. Я Ланина.

Сколько тайн и загадок несёт в себе простой лист бумаги. И самое удивительное – то, что он всегда рядом. Ведь недаром говорят, что всё гениальное – просто. Листок бумаги мы держим в руках каждый день, не задумываясь над тем, что он является одним из самых важных предметов изучения. Среди множества возможных действий с бумагой особое место занимает операция ее перегибания. Тема складывания и перегибания листа бумаги актуальна во все времена. Этой темой увлекались во все времена, она интересна и занимательна. Складывание фигурок из бумаги имеет многовековую историю и своими корнями тесно связано с культурой Востока. Это японское искусство – оригами. Один из элементов Оригами дает возможность сделать занятия геометрией увлекательными и лучше усвоить учебный материал. Но не только геометрия является тем предметом, где можно применять принципы работы с листом бумаги, это и рисование, физика.

Одним из достоинств этой операции перегибания является то, что ее можно производить, не имея под рукой никаких дополнительных инструментов – ни линейки, ни циркуля, ни даже карандаша. Я выбрала эту тему потому, что сама увлекаюсь рисованием, геометрией и физикой. В своей работе я затрагиваю не только геометрию листа бумаги, но возможность применения листа бумаги для рисования без красок и карандашей, для изучения физических свойств бумаги.

Практические свойства бумаги порождают своеобразную геометрию. Роль линий в этой геометрии будут играть края листа и складки, образующиеся при его перегибании, а роль точек – вершины углов листа и точки пересечения складок друг с другом или с краями листа. Оказывается, возможности операции перегибания листа очень велики. То, что они включают в себя всю геометрию одной линейки, не вызывает сомнений. Но они в определенной степени таят в себе также и возможности циркуля.

На основе выводов, полученных в результате исследований, можно ответить на ряд проблемных вопросов:

Какие свойства имеет бумага? В каких областях применяется бумага, и с какой целью? Какие задачи в геометрии можно решить при помощи листа бумаги без карандаша и линейки? Можно ли нарисовать картину без красок и карандашей?

Выяснить, если бумагарвется, режется, сгибается, горит, стоит, то может ли это свойство применяться в геометрии. Применимы ли свойства листа бумаги для исследования свойств плоских фигур, решения задач на доказательство и построения.

Проанализировать источники литературы по данной теме, провести эксперименты применения листа в различных сферах, а так же для исследования свойств плоских фигур, решения задач на доказательство и построения.

Данное исследование направлено на углубление знаний по геометрии, повышение интереса к предмету, расширение представлений о возможностях применения листа бумаги при построении и доказательстве в геометрии.

Как сделать объемные геометрические фигуры из бумаги, развертки для склеивания: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника

Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.

• Как сделать объемные геометрические фигуры
• Из бумаги
• Из картона
• Развертки куба
• Треугольника
• Прямоугольника
• Цилиндра
• Ромба
• Призмы
• Схемы для вырезания
• Конуса
• Пирамиды
• Шестигранника
• Макета с припусками
• Параллелепипеда
• Трапеции
• Овала
• Шара
• Многогранника
• Параллелограмма
• Шаблоны для склеивания
• Сложных фигур
• 3d
• Октаэдра
• Тетраэдра
• Икосаэдра
• Додекаэдра
• Гексаэдра
• Фигурок из треугольников
• Макеты из бумаги
• Оригами
• Дом
• Животные
• Корабль
• Полигональные чертежи
• Игрушки из фигур
• Геометрические маски
• Карандаш
• Как вырезать и склеить модели из бумаги

Как сделать объемные геометрические фигуры

Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.

Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.

Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.

Из бумаги

Из картона

Развертки куба

Треугольника

Прямоугольника

Цилиндра

Ромба

Призмы

Схемы для вырезания

Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.

Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).

Конуса

Пирамиды

Шестигранника

Макета с припусками

Параллелепипеда

Трапеции

Овала

Шара

Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.

Материал, из чего можно сделать плотный шар — картон или плотная бумага.

Многогранника

Параллелограмма

Шаблоны для склеивания

Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.

Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.

Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.

Сложных фигур

3d

Октаэдра

Тетраэдра

Икосаэдра

Додекаэдра

Гексаэдра

Фигурок из треугольников

Макеты из бумаги

Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.

Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.

Оригами

Дом

Животные

Корабль

Применяется множество вариантов, как сделать кораблик из бумаги.

Простая схема.

Полигональные чертежи

Игрушки из фигур

Геометрические маски

Карандаш

Как вырезать и склеить модели из бумаги

Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.

Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.

На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.

Основные ошибки при работе с моделями:

• Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.

Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.

Как найти периметр ромба?

Ромб – это параллелограмм, четыре стороны которого равны друг другу. Его можно интерпретировать как равносторонний четырехугольник. Противоположные стороны ромба параллельны друг другу, а его противоположные углы равны. Диагонали ромба пересекаются под углом 90 ^o и делят углы при вершине поровну. Квадрат также можно назвать ромбом, поскольку он удовлетворяет всем своим свойствам.

 

На приведенном выше рисунке изображен ромб ABCD со сторонами AB, BC, CD и AD равной длины и диагоналями AC и BD, делящими друг друга на две равные части.

Формула периметра ромба

Периметр ромба равен сумме длин всех его сторон. Поскольку все стороны ромба равны друг другу, его периметр определяется как четыре длины его стороны. Например, если одна сторона ромба имеет размер x единиц, его периметр равен 4x единицам.

P = 4a

где

P — периметр ромба,

a — сторона ромба.

Примеры задач

Задача 1. Найдите периметр ромба, если длина его стороны 4 м.

Решение:

Имеем, a = 4.

Используя формулу получаем,

P = 4a

= 4 (4)

= 06 06 02 Задача 2. Найти периметр ромба, если длина его стороны 7 м.

Решение:

Имеем, a = 7.

Используя формулу получаем,

P = 4a

= 4 (7)

= 28 м

Задача 3. Найти периметр ромба, если длина его стороны 10 м.

Решение:

Имеем, a = 10.

Используя формулу получаем,

P = 4a

= 4 (10)

5 2 7 0 90

0 = 4 (10)

0002 Задача 4. Найти периметр ромба, если длина его стороны 12 м.

Решение:

Имеем a = 12,

Используя формулу получаем,

P = 4a

= 4 (12)

= 48 м

Задача 5. Найдите длину стороны ромба, если его периметр равен 96 м.

Решение:

Имеем, P = 96

Используя формулу получаем,

P = 4a

=> a = P/4

5

=/4 a 2 = > a = 24 м

Задача 6. Найдите длину стороны ромба, если его периметр равен 52 м.

Решение:

Имеем, P = 52

Используя формулу получаем,

P = 4a

=> a = P/4

=/4 =/4 a = > a = 13 м

Задача 7. Найдите длину стороны ромба, если его периметр равен 100 м.

Решение:

Имеем, P = 100

Используя формулу получаем,

P = 4a

=> a =/ P/4

0 => a4 00200005

=> a = 25 м

Последнее обновление: 30 апр, 2022

Нравится статья

Сохранить статью

Объяснение линий симметрии параллелограмма! — Мэшап Математика

Каждый урок или курс геометрии будет включать в себя глубокое изучение свойств параллелограммов. В этом посте мы быстро рассмотрим ключевые свойства параллелограммов, включая их стороны, углы и соответствующие отношения.

Наконец, мы определим, имеет ли параллелограмм линейную симметрию. И, если параллелограмм имеет линейную симметрию, как будут выглядеть линии симметрии параллелограмма (в виде диаграммы).

Прежде чем мы ответим на эти ключевые вопросы, связанные с симметрией параллелограммов, давайте кратко рассмотрим свойства параллелограммов:

 Что такое параллелограмм?

 Определение: Параллелограмм — это особый вид четырехугольника (замкнутая четырехсторонняя фигура), в котором противоположные стороны параллельны друг другу и имеют одинаковую длину.

Кроме того, внутренние противоположные углы любого параллелограмма имеют одинаковую величину. А любая пара смежных внутренних углов в параллелограмме является дополнительной (в сумме они равны 180 градусам).

 На следующей диаграмме показаны основные свойства параллелограммов:

 

Линии симметрии параллелограмма

 

Теперь, когда вы понимаете основные свойства и отношения углов параллелограмма, вы готовы исследовать следующие вопросы:

•  Имеют ли параллелограммы линейную симметрию?

• Сколько осей симметрии в параллелограмме?

• Если у параллелограмма нет осей симметрии, то почему у параллелограмма нет осей симметрии?

Для начала отметим, что линия симметрии — это ось или воображаемая линия, которая может проходить через центр фигуры (обращенной в любом направлении) таким образом, что она разрезает фигуру на две равные половины, которые являются зеркальными.

изображения друг друга.

Например, квадрат, прямоугольник и ромб имеют линейную симметрию , потому что по крайней мере одна воображаемая линия может быть проведена через центр фигуры, которая разрезает ее на две равные половины, которые являются зеркальными отражениями друг друга.

На самом деле фигура может иметь несколько линий симметрии. На приведенной ниже диаграмме видно, что квадрат имеет четыре оси симметрии, а прямоугольник и ромб — только две оси симметрии.

А параллелограмм?

  Получается, что у параллелограмма , а не нет осей симметрии.

Но почему у параллелограмма нет осей симметрии? Потому что для любого параллелограмма невозможно построить линию симметрии (ось или воображаемую линию, проходящую через центр фигуры и разрезающую изображение пополам, где каждая сторона является зеркальным отражением другой).

 Вы можете попытаться построить линию симметрии на любом параллелограмме, и вы увидите, что это невозможно.

 На рисунке ниже показано, почему общее количество линий симметрии в параллелограмме равно нулю.

Имеет ли параллелограмм вообще какую-либо симметрию?

Хотя параллелограммы не имеют линейной симметрии, они обладают вращательной симметрией!

В геометрии вращательная симметрия относится к ситуации, когда форма или фигура точно такие же, как их прообраз после того, как они были повернуты на несколько градусов.

Параллелограмм обладает вращательной симметрией, поскольку та же самая фигура появится после поворота оригинала или прообраза на 180 градусов.

На рисунке ниже показано, почему параллелограммы обладают вращательной симметрией.

 

Заключение

На сегодняшнем уроке мы исследовали линии симметрии параллелограмма, независимо от того, существуют ли они, и обладают ли параллелограммы вообще симметрией.

 После рассмотрения свойств параллелограммов, а именно того, что они являются четырехугольниками, у которых противоположные стороны и противоположные углы равны, мы решили определить, обладают ли параллелограммы линейной симметрией.

Применяя определение линии симметрии, мы пришли к выводу, что, хотя такие фигуры, как квадраты и прямоугольники, действительно имеют линии симметрии, параллелограммы не имеют линий симметрии.

Параллелограммы имеют нулевые линии симметрии, потому что невозможно провести через центр любого параллелограмма линию, которая делит фигуру на две равные половины, являющиеся зеркальным отражением друг друга.

Однако, несмотря на то, что параллелограммы не имеют линейной симметрии, они обладают вращательной симметрией, поскольку любой параллелограмм после поворота на 180 градусов приведет к точно такому же изображению, с которого вы начали.

Поделитесь своими мыслями, вопросами и предложениями в разделе комментариев ниже!

(Никогда не пропустите блог Mashup Math — нажмите здесь, чтобы получать нашу еженедельную рассылку!)

Автор: Энтони Персико0290 MashUp Math и советник кампании Amazon Education « With Math I Can ». Вы часто можете увидеть, как я с радостью разрабатываю анимированные уроки математики, которыми я делюсь на моем канале YouTube  . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.

Вам также может понравиться…

18 апреля 2023 г.

Игра «Бумажный самолетик: забавный проект для учащихся»

18 апреля 2023 г.

18 апреля 2023 г.

13 апреля 2023 г.

Какая самая простая математика в колледже?

13 апреля 2023 г.

13 апреля 2023 г.

4 апреля 2023 г.

Как привлечь учащихся к урокам математики — 5 идей

4 апреля 2023 г.