Как сделать куб из бумаги – несколько простых советов
Как сделать куб из бумаги? Существует два способа быстро и легко создать этот равносторонний бумажный шестигранник.
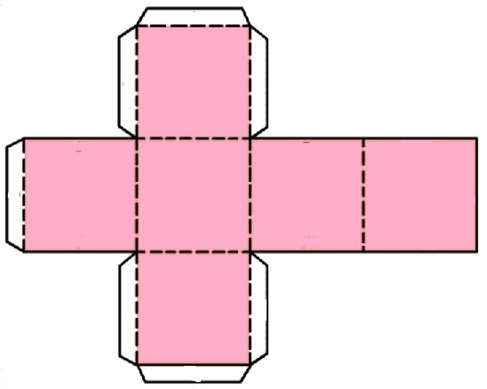
Первый метод – сначала начертить и вырезать развертку куба, а затем склеить ее.
Если данный способ вам подходит, нужно подготовить необходимые инструменты и приспособления. Для того чтобы сделать развертку, понадобится бумага, карандаш, линейка, а также ножницы и клей. Этот набор канцелярских принадлежностей, без сомнения, найдется у каждого, кому необходимо изготовить куб из бумаги.Схема объемного шестигранника очень проста. Первоначально нужно начертить фигуру в форме креста и разделить ее на шесть одинаковых по размеру квадратов таким образом, чтобы одна сторона креста была вдвое длиннее любой другой. Следует обратить внимание на то, что с внешних сторон каждого квадрата должны быть неширокие полоски.
При помощи этих полосок, аккуратно склеить фигуру получится легко. Это и есть один из способов того, как сделать куб из бумаги.
Второй способ не требует использования каких-либо специальных приспособлений. Техника, при помощи которой можно создать этот многоугольник, называется оригами. Как сделать куб из бумаги, используя оригами? Это отнюдь не сложно. Начинать складывать шестигранник необходимо из квадратного листочка бумаги. Прежде всего следует сложить лист в стандартную фигуру оригами – двойной треугольник. Такая фигура получится, если сложить бумагу пополам, сделав из квадратного листка прямоугольный, а затем снова сложить его, опять получив квадрат. После этого раскрываем полученную фигуру таким образом, чтобы с обеих сторон получился треугольник. Это первый из ответов на вопрос о том, как сделать кубик из бумаги, используя оригами.
Затем необходимо произвести еще несколько манипуляций с двойным треугольником.
Его края с обеих сторон надо загнуть к вершине. Снова получился квадрат, противоположные углы которого складываем к центру. Итак, мы сделали шестиугольник, у которого с каждой стороны есть по два кармана.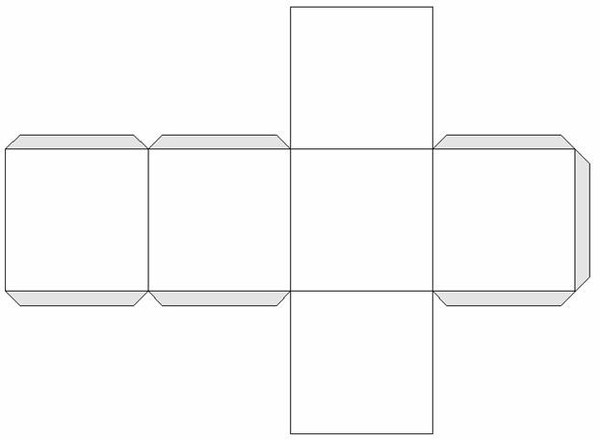 В них необходимо загнуть две половинки бумаги при вершине фигуры. Далее берем иголку и проделываем небольшую дырку в вершине шестиугольника, а затем в нее надо сильно дунуть. Вот и получается нужное объемное тело.
В них необходимо загнуть две половинки бумаги при вершине фигуры. Далее берем иголку и проделываем небольшую дырку в вершине шестиугольника, а затем в нее надо сильно дунуть. Вот и получается нужное объемное тело.
Существует еще одна технология изготовления куба при помощи оригами. Но для нее требуется шесть листков бумаги, которые складываются в определенную форму, а затем собираются в кубик. Соответственно, чем больше материалов используется, тем менее рационален способ изготовления объемного тела, поэтому данный метод оригами мы не описываем. Два варианта, которые были рассмотрены выше, менее трудоемки, а значит, идеально подходят.
Теперь вы знаете два удобных способа того, как сделать куб из бумаги очень быстро и без лишних усилий. Но свои теоретические навыки можно отработать только на практике, поэтому возьмите квадратный листочек бумаги, необходимые приспособления, и сделайте этот красивый шестигранник, который можно использовать не только как наглядное пособие, но и как украшение интерьера!
Базовая форма: двойной квадрат оригами
Двойной квадрат оригами – первый способ
Подготовьте квадратный лист бумаги и следуйте пошаговой инструкции:
- Квадрат сложите пополам горизонтально.

- Разверните.
- Сложите пополам вертикально.
- Разверните.
- Переверните заготовку.
- Сложите по диагонали.
- Раскройте.
- Снова согните по диагонали в другую сторону.
- Раскройте.
- Сформируйте по намеченным линиям двойной квадрат.
Важно обратить внимание на складки долиной и горой. Если все сделано правильно, фигура складывается практически сама по себе. Если сгибы перепутаны, будет сложнее добиться ровного квадрата.
Получилось?
ДаНет
Второй способ
Пошаговая инструкция:
- Расположите квадрат вершиной к себе.
- Сложите по диагонали вверх.

- Согните треугольник пополам направо.
- Правый угол верхнего слоя раскройте, вершину совместите с верхним углом.
- Переверните заготовку.
- Повторите с правым углом.
- Базовая форма готова.
Классические фигурки оригами складываются только из квадратного листа бумаги. Возможность сложить из квадрата предмет, затем вернуться к основе и сложить другой предмет указывает на взаимопроникновение и единство земных форм бытия, согласно буддийской философии. В связи с этим и целостность квадрата нарушать нельзя.
Третий способ
Лилия на основе двойного квадрата
Подготовьте базовую форму. Изнаночная сторона должна быть снаружи.
Изнаночная сторона должна быть снаружи.
Пошаговая инструкция:
- Расположите заготовку свободным краем вверх.
- Правый угол верхнего слоя сложите налево на 2/3.
- Повторите с левым углом.
- Верхняя часть должна перекрывать нижнюю.
- Разверните последние складки.
- Откройте боковой карман справа.
- Прижмите и разгладьте.
- Повторите слева.
- Боковые углы правого элемента сложите к середине. Разверните.
- Раскройте клапан, края сложите к центру.
- Должен получиться ромб.
- Повторите действия для трех остальных сторон заготовки.
- Аккуратно раскройте лилию.
- Лепестки подкрутите карандашом.
Похожий способ складывания лилии:
Как сделать куб из картона схема — MegaMaster. info
info
Содержание статьи
Как сделать куб из картона схема
Геометрический куб, является правильной и простой фигурой. Если не касаться геометрии, то коробки в форме куба используют для упаковки товаров и подарков. Если вам нужно вручить красиво упакованный подарок или обучить своего ребенка, совсем необязательно покупать магазинные коробки, ведь их легко сделать самостоятельно, используя для этой цели картон. Как сделать куб из картона разберём в нашем материале.
Интересное о кубиках
Детские магазины сейчас забиты, разными игрушками, в число, которых входят и развивающие. В магазинах можно найти игрушку, которая вам необходима по соответствующей для вас стоимости и для разного возраста. Вот кубики, для детей найти трудно.
Увлекательные игрушки, хорошо развивают у ребенка, координацию, воображение, мышечную массу рук и мелкую моторику. Магазинные кубики изготовляют из разного материала, но мы предлагаем узнать, как сделать кубик из картона.
Используя куб можно сделать домик из картона для игры в куклы.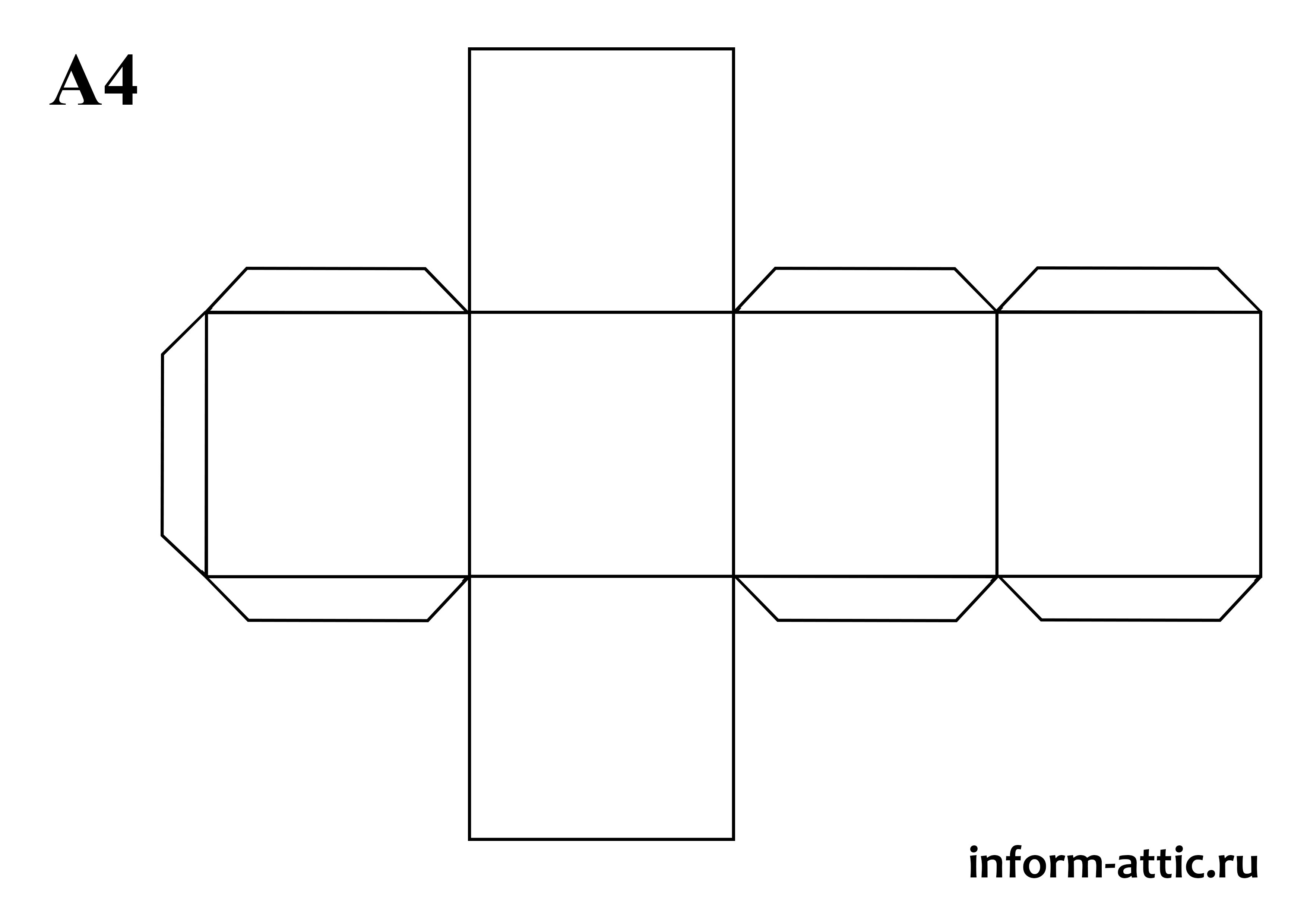 А добавив к фигуре конус из картона, получаем башню настоящего замка. На готовых кубиках можно нарисовать или наклеить изображения животных из журналов и газет, написать красивые буквы и цифры. Независимо, что будет изображено на кубике, изделия значительно облегчат подготовительные занятия ребенка к школе. Вы сможете выучить алфавит, названия животных и цифры.
А добавив к фигуре конус из картона, получаем башню настоящего замка. На готовых кубиках можно нарисовать или наклеить изображения животных из журналов и газет, написать красивые буквы и цифры. Независимо, что будет изображено на кубике, изделия значительно облегчат подготовительные занятия ребенка к школе. Вы сможете выучить алфавит, названия животных и цифры.
Не менее популярны и упаковки. Картонные коробки в виде куба, используют и для упаковки товара. А в изготовленный и украшенный вариант кубика, можно положить подарок, и презентовать его на предстоящие торжество друзей или родных.
Ранее, рассматривая поделки оригами для детей, мы изучали информацию о том, как сделать бумажный кубик, сегодня поговорим о картонном. Перед информацией о том, как сделать кубик из картона, нужно разобраться, что, необходимо для изготовления. Инструмент и материал:
- канцелярский нож и ножницы;
- обычный или цветной картон;
- клей;
- простой карандаш и линейка.

Список, маленький, но у вас получится сделать из таких материалов, прекрасную картонную упаковку для подарка или же кубик для игры и обучения своего ребенка.
Детский кубик
Кубик приходит, кстати, если запланирована интересная настольная игра. Игрушки можно сделать и развивающими, прилагаем фантазию и терпение. Рассмотрим способ изготовления кубика. Изготовляется он так:
- скачиваем или изготовляем шаблон;
- распечатываем его;
- вырезаем схему по линиям;
- в точности переносим его на картон;
- вырезаем из картона заготовку;
- складываем кубик по линиям;
- склеиваем изделие.
Рекомендуем во время складывания картона в куб, использовать канцелярский нож. Если надрезать изгиб, материал легче гнется, а кубик будет выглядеть более презентабельно и эстетично. Если используете такой совет, то надрезы должны быть изнутри изделия. Так, углы будут ровными, а не выпуклыми.
После склеивания, на боках можно нарисовать цифры или изображения животных. Теперь вы знаете, как сделать куб из картона и можете приступать к обучению ребенка. Если изготовить много таких кубиков, разного размера и цвета, то можно сделать целый алфавит, для ребенка. Кубик можно изготовить в случае потери игрового кубика, на котором выставлялись очки за игру. В этом случае на сторонах, нужно нарисовать цифры.
Теперь вы знаете, как сделать куб из картона и можете приступать к обучению ребенка. Если изготовить много таких кубиков, разного размера и цвета, то можно сделать целый алфавит, для ребенка. Кубик можно изготовить в случае потери игрового кубика, на котором выставлялись очки за игру. В этом случае на сторонах, нужно нарисовать цифры.
Куб для упаковки
Сделать куб из картона совсем несложно. Если вы думаете изготовить подарочную упаковку в форме куба, тогда нужно учитывать некоторые моменты.
Делаем подарочную упаковку:
- Проводим замер выбранного предмета. Нужно узнать ширину высоту подарка. Получив результат, берем самое большое значение, прибавляем к нему несколько сантиметров, чтобы подарок лежал в коробке свободно.
- Берем картон, подходящего размера. На материале чертим развертку куба. Первым делом чертим квадрат со сторонами полученных размеров. К квадрату добавляем еще четыре таких же по размеру квадрата. К любому из квадратов дорисовываем еще один квадрат идентичного размера.

Если кубик будет не обклеен, а цвета картона, то линии карандаша должны быть тонкими, для этого не нажимаем на карандаш, а просто проводим линии.
Когда планируется изготовить упаковку и обклеить ее упаковочной бумагой, развертку лучше вычерчивать более жирно, чтобы хорошо было видно все линии. - Для сборки куба, необходимы специальные клапаны, с их помощью склеивать куб гораздо легче, а итоговый вариант будет иметь эстетичный внешний вид. Чтобы сделать такие клапаны, нужно по бокам нарисованных квадратов начертить полосы. Ширина таких полос зависит от размера кубика, при этом полосы, должны качественно склеиться между собой.
- Начертив шаблон для вырезания куба, линейкой или тупой стороной канцелярского ножа, нужно провести по всем линиям сгибов, при этом немного надавливая на картон. Нужно вырезать заготовку по контуру. На этом этапе важно не отрезать клапаны, иначе придется переделывать свою работу.
- Сгибаем заготовку по линиям внутрь фигуры. Получатся ровные углы на упаковке.

- Вооружаемся клеем. Клей наносим тонким слоем на изготовленные клапаны, склеиваем одну пару квадратов и соединяем все остальные стороны. В том случае если из щелей вытек клей, его, нужно аккуратно убрать с поверхности.
Напомним, если делаете подарочную упаковку, то одну из сторон куба не нужно заклеивать. В этом случае на стороне, которая будет крышкой упаковки, необходимо сделать длинный полукруглый клапан, примерно посередине квадрата. С закрывающейся стороны сделайте выемку. После размещения подарка язычок вставляется в выемку и получается запечатанная упаковка, которую легко открыть и не повредить.
Вы знаете, как сделать куб из картона и решили изготовить большой вариант упаковки, а одного листа картона, недостаточно, то заготовку нужно разбить на несколько частей. На этих частях, нужно дополнительно нарисовать соединительные клапаны.
Но не стоит разделять куб по граням. Разделив по грани, куб получится с видимыми соединениями, и будет иметь непрезентабельный внешний вид. Если, необходим кубик очень большого размера, его необходимо изготовлять, используя шесть отдельных квадратов с клапанами. В завершение склеиваются квадраты в большой куб.
Если, необходим кубик очень большого размера, его необходимо изготовлять, используя шесть отдельных квадратов с клапанами. В завершение склеиваются квадраты в большой куб.
Ещё куб можно сделать в виде коробочки по технике оригами
Как сделать пирамиду из бумаги. Пошаговые инструкции + 300 фото
пирамида из бумаги своими рукамиЕсли вы новичок в оригами, для вас это отличный проект. Сделать пирамиду из бумаги очень легко. Форма пирамиды, с одной стороны, простая геометрическая фигура, но выступает как символ фундаментального архитектурного строительства.
Создание трехмерной бумажной пирамиды
предполагает более глубокое понимание геометрии и архитектуры древних египетских пирамид. Чтобы сделать модель пирамиды оригами, вам понадобятся только бумага, а для поделки еще и основные школьные принадлежности.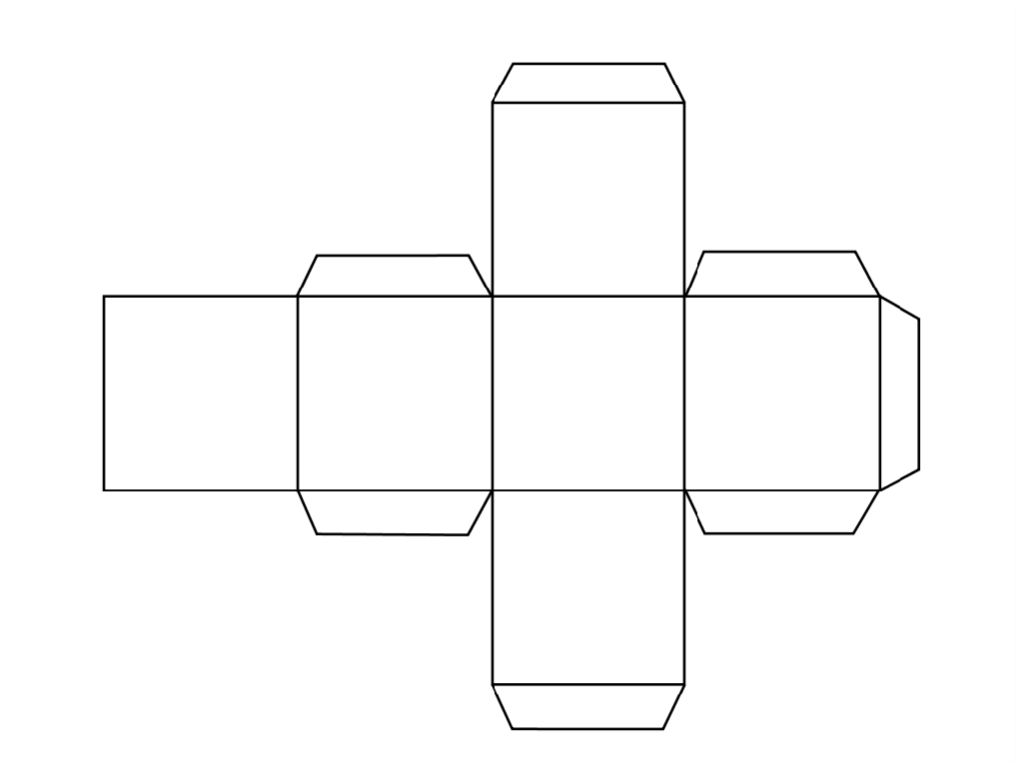 В зависимости от проекта, такая поделка может дополнить диораму, стать украшением или даже послужить подарочной коробочкой.
В зависимости от проекта, такая поделка может дополнить диораму, стать украшением или даже послужить подарочной коробочкой.
Пирамида из бумаги своими руками
Любой землянин может сделать пирамиду из бумаги, поэтому автор не претендует на исключительность. Нарисуйте пирамиду, как показано на первом фото. Длина базовых линий и лепестков пирамиды составляет 4 см, возле лепестков есть небольшое (0,5 см) удлинение. Теперь возьмите ножницы и вырежьте рисунок. Сложите линии лепестков у основания пирамиды, сгибая лепестки (0,5 см). Нанесите клей.
Поднимите лепестки и соедините, сложив мини-лепестки (0,5 см). Это все. Как видите, очень простая задача, и вы можете создать множество
Источник фото: www.instructables.com/id/Pyramid-with-paper/
Объемная пирамида из бумаги
Вы когда-нибудь хотели красивое украшение стола или идею подарка, не тратя много денег? Пресс-папье и рамы для картин просто слишком дорогие и скучные для размещения в офисе. К счастью, есть простое (и дешевое) решение! Вы можете сделать объемную модель 3D пирамиды из бумаги, используя расходные материалы, которые, вероятно, уже у вас есть. Этот проект не только великолепен в качестве декорации, но и является отличной поделкой для детей. Можно подарить кому-то в качестве подарка или открытки! Так что посмотрите мастер класс на пошаговых фото и сделайте эту красивую пирамиду из бумаги
К счастью, есть простое (и дешевое) решение! Вы можете сделать объемную модель 3D пирамиды из бумаги, используя расходные материалы, которые, вероятно, уже у вас есть. Этот проект не только великолепен в качестве декорации, но и является отличной поделкой для детей. Можно подарить кому-то в качестве подарка или открытки! Так что посмотрите мастер класс на пошаговых фото и сделайте эту красивую пирамиду из бумаги
Источник фото: www.instructables.com/id/Paper-3D-Pyramid/
Египетская пирамида из бумаги
Пример, как сделать мини-пирамиду, используя печатный шаблон египетской пирамиды (можно скачать на сайте, ссылка под галереей). Вырежьте шаблон. Не беспокойтесь, если края не идеальны, просто не отрезайте ни одной точки треугольника. Разрежьте остальные грани пирамиды точно таким же образом. Аккуратно сложите нижний квадрат и боковые клапаны, используя темные линии треугольника в качестве ориентира. Возьмите два кусочка скотча, чтобы соединить две грани пирамиды вдоль одного края. Самый простой способ — положить два треугольника вплотную с зажатыми между ними боковыми клапанами, а затем сложить ленту по внешнему краю.
Самый простой способ — положить два треугольника вплотную с зажатыми между ними боковыми клапанами, а затем сложить ленту по внешнему краю.
Затем скрепите два клапана вместе на внутренней стороне. (Или можете склеить, тогда не нужна лента снаружи!). Скрепите все четыре стороны. Когда добавляете новый треугольник, можете сложить его вплотную с одним рядом, чтобы помочь выстроить их в ряд. Присоединиться к последним двум немного сложно, поэтому при приклеивании внешнего края сожмите внутренние клапаны вместе. Сложите нижние квадраты так, чтобы каждый закрывал нижний. Только приклейте последний (самый внешний) один к одному под ним. И вы сделали
Источник фото: feltmagnet.com/crafts/how-to-make-an-egyptian-pyramid
Как сделать пирамиду из картона
Хотите научиться делать поделки из картона? Этот материал предоставляет безграничные возможности … Вам просто нужно следовать пошаговым фото, и вы узнаете, как сделать пирамиду из картона своими руками.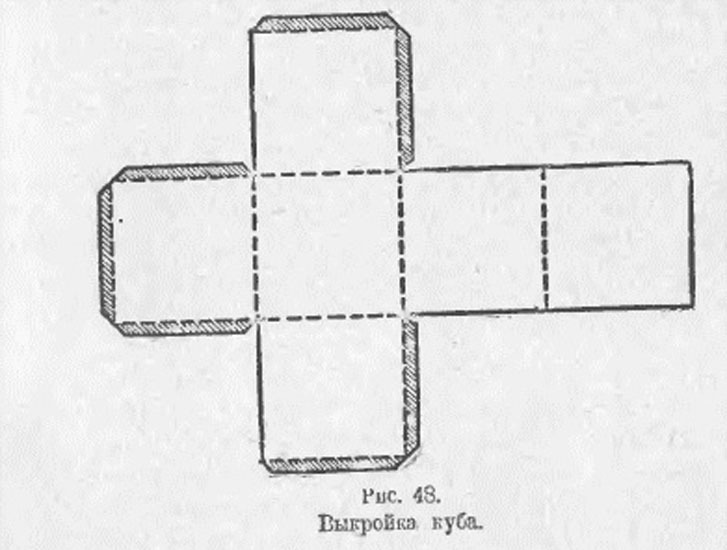 Это простая поделка, которую легко и быстро сделать, такое занятие наверняка понравится детям. Вы можете сделать несколько пирамид из бумаги, например, разного цвета.
Это простая поделка, которую легко и быстро сделать, такое занятие наверняка понравится детям. Вы можете сделать несколько пирамид из бумаги, например, разного цвета.
Попробуйте и посмотрите, как это просто!
Источник фото: arts.onehowto.com/article/how-to-make-a-pyramid-out-of-cardboard-336.htmla
Треугольная пирамида из бумаги
Пирамида может иметь много граней, вы можете сделать пирамиды с разными основаниями, например треугольную пирамиду из бумаги или восьмиугольную пирамиду. Здесь же показано, как сделать треугольную пирамиду из бумаги. Вам понадобиться шаблон (или просто возьмите карандаш, линейку и нарисуйте самостоятельно), ножницы, клей, бумага или картон. Скопируйте шаблон треугольной пирамиды на бумагу и вырежьте ножницами. Сложите его по всем линиям шаблона. Попробуйте установить пирамиду с треугольным основанием, прежде чем наносить клей, чтобы не думать о том, куда пойдет каждая вкладка. Нанесите клей на одну из вкладок и приклейте на место.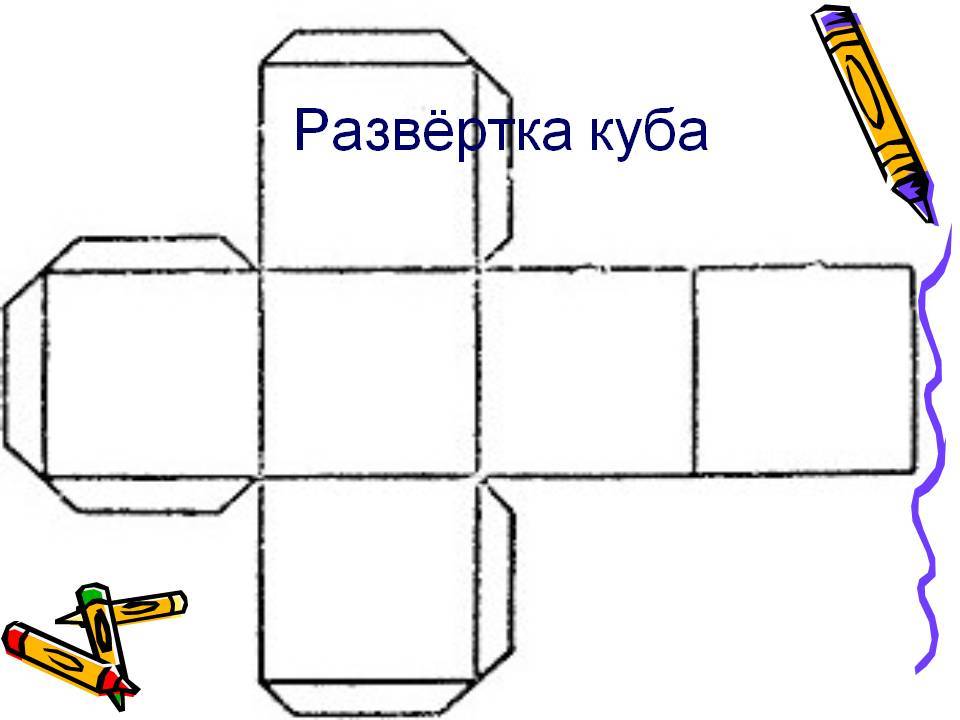
Источник фото: arts.onehowto.com/article/how-to-make-a-triangular-pyramid-out-of-cardboard-4567.html
Бумажная пирамида
Это руководство разработано для учеников средней школы. Создавая совершенную пирамиду из бумаги, ученики развивают способность пользоваться линейкой и демонстрировать точность. Это довольно простой проект. Пирамида имеет квадратное основание, что означает, что у нее будет 4 стороны треугольной формы. Как сделать пирамиду из бумаги, показано на пошаговых фото, но если хотите научить детей, прочитайте рекомендации, которые содержаться в подробной инструкции на сайте.
Источник фото: www.instructables.com/id/Perfect-Paper-Pyramid-More-practice-with-project-/
Восьмиугольная пирамида из бумаги
Здесь показано, как сделать пирамиду из бумаги с восьмиугольной основой.
Вам понадобиться шаблон, ножницы, клей и бумага.
- Первый шаг — скопируйте шаблон для пирамиды с восьмиугольным основанием.
- Используйте бумагу или картон, как хотите.
- Сложите по всем линиям шаблона.
- Попробуйте установить восьмиугольное основание, прежде чем использовать клей, чтобы было ясно, куда пойдут вкладки.
- Нанесите клей и приклейте одну из вкладок.
- Зажмите пальцами, чтобы закрепить конструкцию.
- Сделайте то же самое с остальными.
Вот и все, в принципе ваша восьмиугольная пирамида из бумаги закончена!
Источник фото: arts.onehowto.com/article/how-to-make-a-pyramid-with-an-octagonal-base-7696.html
Пирамида оригами
Эту простую пирамиду оригами сложить очень легко, всего очень 11 шагов.
Здесь используется известная техника оригами основания воздушного шара, если вы с ней знакомы, то у вас точно проблем не будет.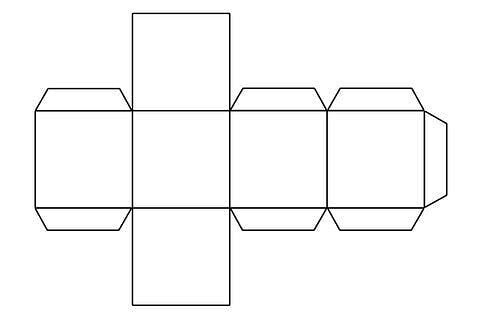
Источник фото: www.origami-make.org/simple-origami-pyramid.php
Пирамида оригами схема
Эта инструкция для тех, кто хочет сложить Великую пирамиду оригами.
Великая пирамида имеет уклон 51 °. Эта модель оригами имитирует знаменитое сооружение. Для изготовления используется техника оригами основания воздушного шара. Размер бумаги 20см х 20см.
Как сделать куб из бумаги в технике оригами по готовой схеме.
Задумывались ли вы о том, как сделать куб из бумаги и зачем это нужно? Допустим, как сделать кубик из картона своими силами, мы вам расскажем и даже покажем. А какими полезными функциями вы наделите кубик оригами? Подскажем: вспомните свои детские кубики с буквами, из которых вы учились складывать первые слова, еще не умея писать. А если бумажный кубик оклеить картинками из старых детских книжек, получится не менее интересный, чем в нашем далеком детстве, пазл-конструктор.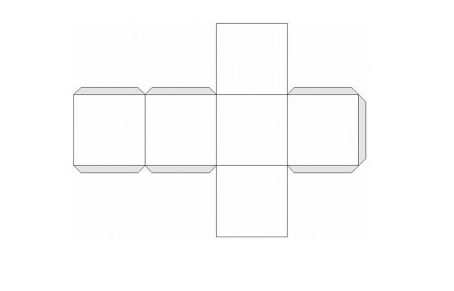
Вариантов игрового применения куба из цветной бумаги не счесть. И при этом не придется переживать, что дети поранят друг друга, кидая такую игрушку. Наши-то деревянные были потяжелее. Мы уже готовы показать, как сделать кубик из бумаги своими руками прямо сейчас. Готовы приступать?
Простой бумажный кубик
Объемный шестигранный куб 3Д складывают из квадратного листка бумаги без клея. И даже ножницы здесь не потребуются. Разве что отрезать лишний «хвостик» от листа А4, чтобы получить заготовку-квадрат. Зато пригодится навык надувания воздушных шариков, ведь мы сейчас научим вас тому, как сделать надувной кубик. Заинтригованы? Тогда начнем:
- Схема 1 — ваш наглядный ориентир. К нему следует прибегать каждый раз, когда алгоритм складывания кажется сложным. Возьмите бумажный квадрат и сложите его по диагоналям, затем пополам — все это просто разметка;
- Ориентируясь на диагонали-сгибы, сформируйте треугольник, подгибая внутрь боковые плоскости заготовки (см. схему). 4 гуляющих угла у основания треугольника нужно подогнуть к вершине по 2 с каждой стороны заготовки;
- Боковые противоположные уголки подогните к центру — у вас здесь есть вертикальная ось-ориентир. Повторите действие с другой стороны. Гуляющие уголки одного из конических выступов (на втором углы «закрыты») дважды подгибают, чтобы их можно было аккуратно заправить в срединные уголки-кармашки;
- Аналогично заправьте дважды сложенные уголки в кармашки с обратной стороны заготовки. Модель куба готова, осталось дать ей объем. Найдите открытый уголок и через него надуйте макет.
Куб из модулей: сборный кубик 6 цветов
Как сделать кубик из картона своими силами мы уже рассмотрели выше, а для этого модульного куба будет достаточно разноцветной бумаги 6-ти расцветок (или 3-х повторяющихся). Он и без картона получится достаточно плотным за счет алгоритма складывания модулей (каждого в отдельности и всех воедино). Давайте начнем разбираться поэтапно. Сразу предупредим, что весь процесс будет разделен на 7 шагов — складывание модулей и сборка куба (можно на клей — будет прочнее). Какое-то время будет потрачено, но результат вас однозначно порадует: кубики получатся яркими, разноцветными, не нуждающимися в дополнительных украшениях или росписи.
- Возьмите квадратный листок бумаги и сложите его так, чтобы получилось видимое разделение на 4 одинаковых прямоугольных плоскости (см. рис. 2). Загните малые уголки по диагональным углам стартового квадрата;
- Заверните «створки» листа подобно закрытию оконных ставней. Используя ориентиры-уголки (подогнутые ранее), загните внутрь незадействованные прежде углы, потом заправите их внутрь с обеих сторон. Получится параллелограмм;
- Переверните конструкцию вниз лицом, отогните уголки к себе так, чтобы получился маленький квадрат с треугольными ушками-отгибами. Сделайте еще 5 шт. таких модулей.
Соединяйте блоки в куб, вводя уголки модулей в срединные плоскости-кармашки соседних блоков. Проявите смекалку, в крайнем случае поможет схема. Как сделать оригами кубик из ярких модулей, вы освоили на практике. Попробуйте склеить куб из блоков на этапе сборки, чтобы он был еще прочнее и не рассыпался на модули в игре. Можно, конечно, взять стандартную развертку куба, просто распечатать ее и склеить — готовые шаблоны всегда под рукой. А если типовая выкройка вас не устраивает и в игру нужен оригинальный счетный кубик, вы на раз-два сможете его сложить сами. Чего проще, когда знаешь, как сделать из бумаги еще и не такие премудрости. Возможно, вас заинтересуют схемы складывания бумажной гадалки или лягушки, которая открывает рот.
Как сделать кубик из бумаги
Играть в кубики любят все дети без исключения. Особенной популярностью пользуются кубики с буквами и животными. Самое интересное – такую полезную игрушку можно сделать самостоятельно и привлечь ребенка. Как сделать кубик из бумаги? Читайте дальше и вы найдете простые и сложные схемы его создания.
Содержание:
- Простой бумажный кубик оригами
- Модульный сборный куб из 6 цветов
- Схемы и шаблоны для печати
- Видеоинструкции
Простой бумажный кубик оригами
Способ 1
Для того, чтобы сложить объемный куб с шестью гранями, вам понадобится лист бумаги квадратной формы и все. Работа происходит без клея. А ножницами, вы сможете воспользоваться один раз, когда нужно будет срезать выступающий за край материал. Кроме этого, когда процесс изготовления подойдет к концу, понадобится много воздуха из ваших легких для надувания. Но все по порядку.
Ход работы:
- Берем лист бумаги А4, складываем по диагонали и отрезаем лишнее. Получается квадрат. Далее этот квадрат снова складываем по диагонали, а после – вдвое. Этими движениями мы намечаем линии сгиба;
- По схеме, учитывая диагональные линии, делаем треугольную фигуру, подворачиваем во внутрь оба края слева и справа. Углы, которые оказались свободные, возле основания геометрической фигуры подгибаем в сторону вершины. Делаем это со всех сторон треугольника;
- В центр подгибаем противоположные углы сбоку. Ориентироваться нужно на вертикальную линию. То же самое делаем и со второй стороной. Подгибаем также 2 раза свободные углы там, где выступ конической формы, а затем осторожно засовываем в углы-карманчики;
- Такие же действия с загибаем и заправлением в кармашки уголков повторите с другой стороны;
- Получился кубик в сложенном состоянии. Чтобы придать ему форму 3D, ищем открытый угол и вдуваем туда воздух.
Способ 2
Перед началом работы найдите плотную бумагу, линейку, простой карандаш, клей, ножницы.
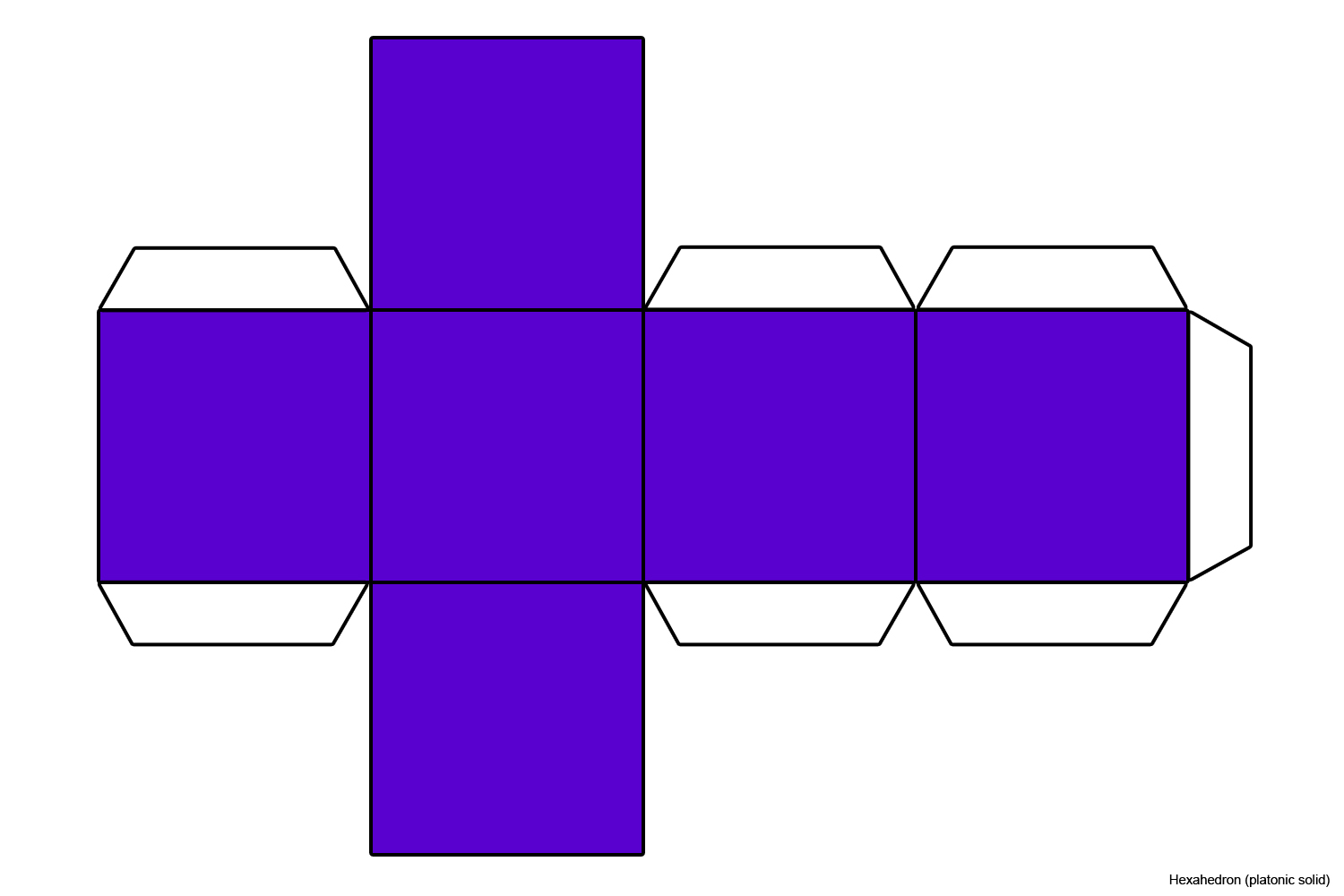
Можно воспользоваться готовым шаблоном, а можно нарисовать такой шаблон самому, соблюдая размеры. Стоит лишь взять карандаш и начертить 4 квадрата один за другим вертикально, а затем еще 2 квадрата с двух сторон. Не забудьте оставить немного места для склеивания.
Теперь вырежьте все по линиям и осторожно согните намеченные линии, чтобы образовались грани. Смажьте клеем и соедините стеночки куба между собой.
Модульный сборный куб из 6 цветов
Перед началом работы приготовьте 6 листов бумаги различных цветов (можно взять 2 листа одного цвета, 2 листа другого, 2 листа третьего цвета). Картон здесь можно не применять, потому как за счет многоразового соединения модулей получится довольно плотная конструкция. Вы должны быть готовы к тому, что придется потратить немало время, но результат того стоит. Стоит лишь четко следовать схеме и соблюдать все этапы поочередно.
Как делать?
- На квадратном бумажном листе складываем линии сгиба: сначала пополам, а потом каждую плоскость делим еще на две. Далее следует завернуть правый нижний угол и левый верхний.
- Сложите нижнюю часть к центру, а затем верхнюю. Ориентир – горизонтальная линия посередине. Заверните вовнутрь те углы, которые мы не трогали на предыдущем этапе с одной, и с другой стороны. Должна получится фигура, похожая параллелограмм.
- Положите заготовку лицом на поверхность, а углы выгните к себе. Вы увидите небольшой квадрат с отогнутыми уголками. Повторите конструкцию модулей еще 5 раз.
- Соедините все элементы в единую конструкцию. Для этого заправляйте уголки каждого модуля в плоскости-ниши посередине, расположенные на элементах рядом.
Не забывайте пользоваться схемой, на которой расписано ясно и четко все по шагам.
Совет! Чтобы кубик держался долго, получился крепким, элементы не выпадали и не высовывались уголки, зафиксируйте все клеем. Только пользоваться им нужно в меру и на этапе сборки поделки.
Схемы и шаблоны для печати
Видеоинструкции
Конечно, видеоуроки всегда спасают в том деле, которым вы решили заняться впервые. Предлагаем вам следующие наглядные инструкции, которые помогут сделать оригинальные кубики из бумаги самостоятельно.
Модульный кубик оригами
Движущиеся кубики из бумаги
Здесь мы рассмотрим таблицы, интеллект-карты и четыре различных типа диаграмм: круговые диаграммы, гистограммы, диаграммы Ганта, блок-схемы и графики. A. Таблицы Набор рисунков лучше всего можно передать с помощью таблиц. Б. Круговые диаграммы
C. Столбчатые диаграммы Горизонтальные стержни
Перпендикулярная гистограмма Перпендикулярная гистограмма также является составной гистограммой, поскольку она включает разбивку по отдельным продуктам в каждой полосе. Диаграммы Ганта Разновидностью гистограммы является диаграмма Ганта, используемая в сочетании с процесс контроля в бизнесе. Это дает мгновенное визуальное сравнение ожидаемой и фактической производительности. E. Графики Наиболее распространенной формой визуального представления является граф. Графики двухмерные. По оси X записывается одно измерение, обычно измерение времени. По оси ординат записывается другой диапазон данных, который изменяется в зависимости от временного (или другого) ряда. Преимущество всех этих схематических представлений состоит в том, что они представляют данные в легко усваиваемой форме. Те, кто вовлечен в бизнес, должны иметь возможность интерпретировать данные, представленные им в любой форме. f) Интеллектуальная карта — это диаграмма, используемая для визуального выделения информации. Ментальная карта часто создается вокруг одного слова или текста, помещенного в центр, к которому добавляются связанные идеи, слова и концепции. Основные категории исходят из центрального узла, а меньшие категории являются подветвями более крупных ветвей. [1] Категории могут представлять слова, идеи, задачи или другие элементы, связанные с центральным ключевым словом или идеей. Интеллектуальные карты можно рисовать вручную, например, в виде «черновых заметок» во время лекции или собрания, или в виде изображений более высокого качества, когда доступно больше времени.Проиллюстрирован пример приблизительной карты разума. Ментальные карты считаются разновидностью паучьей диаграммы. Похожей концепцией 1970-х годов была «идея взрыва солнца». g) Блок-схема — это тип диаграммы, который представляет алгоритм или процесс, показывающий шаги в виде прямоугольников различного типа и их порядок, соединяющий их стрелками. Это схематическое [[представление знаний и рассуждения | представление решения данной проблемы.Операции процесса представлены в этих полях и строках]]; скорее, они подразумеваются последовательностью операций. Блок-схемы используются при анализе, проектировании, документировании или управлении процессом или программой в различных областях. Блок-схема научного метода
подниматься, снижаться, уменьшаться, удваиваться, падать, расширяться, падать, колебаться, спускаться, подниматься, расти, достигать минимума, увеличиваться, подниматься, погружаться, достигать максимума, восстанавливаться, оставаться стабильным, подниматься, стабилизироваться, оставаться тот же
b) Эти выражения комментируют важную информацию в визуальном элементе. Заполните их следующими словами:
1. На диаграмме процентная доля нашей доли пирога, которую показывает рынок 2. Путешествие в 2006 году в соответствии с затратами с тех пор, как резко возросло, необходимо изучить 3.ставка 0,5% в начале года, процентная ставка была увеличена на 4. Июньское повышение на 15%, если транспортные расходы составили .5. Низкая декабрьская доходность 6. Спад из-за плохой ситуации, вызванной экономической ситуацией
Дата: 22.04.2016; посмотреть: 1222 |
Как нарисовать диаграмму классов?
Диаграмма классов — это своего рода диаграмма UML, которая показывает требуемые объекты и отношения между ними. Поскольку он предоставляет подробную информацию о свойствах и интерфейсах классов, его можно рассматривать как основную модель, а другие диаграммы рассматривать как дополнительные модели.
Создание диаграммы классов
Выполните следующие шаги, чтобы создать диаграмму классов UML в Visual Paradigm.
- Выберите Diagram> New на панели инструментов приложения.
- В окне New Diagram выберите Class Diagram .
- Щелкните Далее .
- Введите имя и описание схемы. Поле Местоположение позволяет выбрать модель для сохранения диаграммы.
- Щелкните ОК .
Создание класса
Чтобы создать класс на диаграмме классов, щелкните Class на панели инструментов диаграммы, а затем щелкните диаграмму.
| |
| Создать класс |
Будет создан класс.
| |
| Класс создан |
Создание ассоциации
Чтобы создать связанный класс на диаграмме классов:
- Наведите указатель мыши на исходную фигуру.
- Нажмите кнопку Каталог ресурсов и перетащите ее.
Использование каталога ресурсов - Отпустите кнопку мыши в том месте, где вы хотите создать класс. Если вы хотите подключиться к существующему классу, перейдите к этому классу. В противном случае оставьте пустое место (либо на фоне диаграммы, либо в форме контейнера, например, пакета).
- Если вы подключаетесь к существующему классу, выберите Association из каталога ресурсов.Если вы создаете новый класс, выберите Association -> Class из каталога ресурсов. Если вы хотите создать агрегацию или композицию, выберите вместо этого Aggregation -> Class или Composition -> Class .
Для создания класса - Если вы создаете новый класс, вы должны увидеть класс сейчас, и он связан с исходной фигурой. Введите его имя и нажмите Введите , чтобы подтвердить редактирование.
Создан ассоциированный класс
Чтобы изменить кратность конца ассоциации, щелкните правой кнопкой мыши рядом с концом ассоциации, выберите Multiplicity во всплывающем меню, а затем выберите множественность.
| |
| Изменить кратность |
Чтобы показать направление ассоциации, щелкните ее правой кнопкой мыши и выберите Параметры презентации > Показать направление во всплывающем меню.
| |
| Показать направление |
Стрелка направления отображается рядом с ассоциацией.
| |
| Показанное направление |
Создание обобщения
Для создания подкласса:
- Наведите указатель мыши на суперкласс.
- Нажмите кнопку Каталог ресурсов и перетащите ее.
Использование каталога ресурсов - Отпустите кнопку мыши в том месте, где вы хотите создать подкласс. Если вы хотите подключиться к существующему классу, перейдите к этому классу. В противном случае оставьте пустое место (либо на фоне диаграммы, либо в форме контейнера, например, пакета).
- Если вы подключаетесь к существующему классу, выберите Generalization из каталога ресурсов.Если вы создаете новый класс, выберите Generalization -> Class из каталога ресурсов.
Для создания подкласса - Если вы создаете новый класс, вы должны увидеть этот класс сейчас, и он связан с исходной формой с помощью обобщения. Введите его имя и нажмите Введите , чтобы подтвердить редактирование.
Создан подкласс
Создание зависимости от / до атрибута / операции
Вы также можете добавить зависимость от и / или атрибута или операции в классе.Чтобы создать такую зависимость.
- Выберите Зависимость на панели инструментов диаграммы.
Выбор зависимости - Нажмите на исходную фигуру или на члена класса.
Нажать на исходную операцию - Перетащите к целевой фигуре или к члену класса.
Перетаскивание к целевому атрибуту - Отпустите кнопку мыши, чтобы создать зависимость.
Зависимость, созданная между операцией и элементом
Создание атрибута
Чтобы создать атрибут, щелкните правой кнопкой мыши класс и выберите Добавить > Атрибут во всплывающем меню.
| |
| Создать атрибут |
Атрибут создан.
| |
| Атрибут создан |
Создание атрибута с помощью клавиши ввода
После создания атрибута нажмите клавишу Enter , будет создан другой атрибут.Этот метод позволяет быстро и легко создавать несколько атрибутов.
| |
| Создайте атрибут с помощью клавиши Enter |
Создание операции
Чтобы создать операцию, щелкните класс правой кнопкой мыши и выберите Добавить > Операция во всплывающем меню.
| |
| Операция создания |
Операция создана.
| |
| Операция создана |
Подобно созданию атрибута, вы можете нажать клавишу Enter для непрерывного создания нескольких операций.
Показан только тип параметра
Когда имя параметра начинается с «un named_», его имя не будет отображаться в форме класса, оставив тип параметра (если он определен).
| |
| Параметр без названия |
Переупорядочивание, копирование и перемещение членов класса перетаскиванием
Чтобы изменить положение члена класса, выберите его и перетащите внутрь отсека. Вы увидите толстую черную линию, указывающую, куда будет помещен член класса.
| |
| Повторный заказ члена класса |
Отпустите кнопку мыши, член класса будет переупорядочен.
| |
| Член класса переупорядочен |
Чтобы скопировать член класса, выберите его и перетащите к целевому классу, удерживая нажатой клавишу Ctrl, вы увидите толстую черную линию, указывающую, где будет размещен член класса.Рядом с курсором мыши отображается знак «плюс», указывающий, что это действие копирования.
| |
| Копировать член класса |
Отпустите кнопку мыши, член класса будет скопирован.
| |
| Член класса скопирован |
Чтобы переместить член класса, выберите его и перетащите к целевому классу. Вы увидите толстую черную линию, указывающую, где будет помещен член класса.В отличие от копирования, не нажимайте клавишу Ctrl при перетаскивании, курсор мыши без знака плюс указывает, что это действие перемещения.
| |
| Переместить член класса |
Отпустите кнопку мыши, член класса будет перемещен.
| |
| Член класса переехал |
Выбор всех учеников
Чтобы выбрать всех членов в классе, вы можете сначала выбрать любого члена, а затем нажать Alt-A , чтобы выбрать остальных.
Родственники класса
Отношения, такие как зависимость и общие соединители, могут быть добавлены между атрибутом и операцией классов. Для этого:
- Выберите тип создаваемой связи на панели инструментов диаграммы.
Выбор зависимости - Переместите указатель mosue на исходный элемент.
Создание отношения из члена класса - Нажмите на него и удерживайте кнопку мыши.
- Перетащите на целевой элемент.
Отпустить кнопку мыши на элементе целевого класса - Отпустите кнопку мыши, чтобы создать соединитель. Хотя похоже, что соединитель соединяет классы, но не члены, если вы проверите его спецификацию, вы увидите, что соединитель действительно соединяет элементы.
Связь создана
Создание перечисления и добавление литерала перечисления
Перечисление — это специальный тип данных, который состоит из заранее определенного набора значений, известных как литералы перечисления.Вот некоторые из типичных примеров:
- Цвет (КРАСНЫЙ, ЗЕЛЕНЫЙ, СИНИЙ)
- Ориентация (СЕВЕР, ЮГ, ВОСТОК, ЗАПАД)
- Переключатель (ВКЛ., ВЫКЛ.)
Чтобы создать перечисление в инструменте диаграммы uml, выберите Перечисление на панели инструментов диаграммы и щелкните диаграмму, чтобы создать ее.
| |
| Создать перечисление |
Чтобы добавить литерал перечисления, щелкните правой кнопкой мыши класс перечисления и выберите Добавить> Литерал перечисления во всплывающем меню.
| |
| Добавить литерал перечисления |
Затем введите имя литерала и подтвердите редактирование.
| Введенный числовой литерал |
Набор обобщений
Набор обобщения определяет конкретный набор отношений обобщения, которые описывают способ
, в котором общий классификатор (или суперкласс) может быть разделен с использованием определенных подтипов.Чтобы определить набор обобщений, выберите обобщения, которые нужно включить, щелкните правой кнопкой мыши и выберите Набор обобщений> Создать набор обобщений … во всплывающем меню.
| |
| Создать набор обобщений |
Назовите набор в окне «Управление наборами обобщений» и подтвердите, нажав OK .
| |
| Назовите набор обобщений |
Выбранные обобщения сгруппированы.Отрегулируйте разъем, чтобы схема была аккуратной.
| |
| Отрегулируйте соединитель |
Повторите шаги для других обобщений.
Границы | Метод наименьших квадратов для нестандартных расширений диффузионных карт
1. Введение
В последнее время во многих научных и технологических областях нам необходимо анализировать и обрабатывать многомерные данные, такие как речевые сигналы, изображения и видео, текстовые документы, записи о торговле акциями и другие.Из-за проклятия размерности [1, 2] прямой анализ и обработка данных большой размерности часто невозможны. Следовательно, уменьшение размерности (DR) (см. Книги [3, 4]) становится критическим шагом в обработке данных большой размерности. DR отображает данные высокой размерности в пространство низкой размерности, так что обработка данных может выполняться в их представлении низкой размерности. В литературе существует множество методов DR. Известный линейный метод — анализ основных компонентов (PCA) [5].Однако PCA не может эффективно уменьшить размерность набора данных, который по существу находится на нелинейном многообразии. Поэтому, чтобы уменьшить размерность таких наборов данных, люди используют нелинейные методы DR [6–12], среди которых был доказан метод диффузионных карт (Dmaps), введенный Койфманом и его исследовательской группой [13, 14]. привлекательно и эффективно. Принимая идеи спектральной кластеризации [15, 16] и лапласовских собственных карт [17], Dmaps интегрирует их в более концептуальную структуру — геометрические гармоники.
В качестве спектрального метода Dmaps использует ядро диффузии для определения подобия на заданном наборе данных X ⊂ ℝ D . Основное собственное подпространство d ( d ≪ D ) ядра обеспечивает пространство признаков X , так что диффузное отображение 𝔉 отображает X в набор Y = 𝔉 ( X ), который называется DR X .
Обратите внимание, что отображение 𝔉 строится с помощью спектрального разложения ядра, которое зависит от данных.Если набор X увеличен до X = X ∪ Z и мы хотим сделать DR X с помощью Dmaps, мы должны переобучить набор X , чтобы построить новое диффузное отображение. . Подход к переобучению часто оказывается непрактичным, если мощность X становится очень большой или новый набор данных Z появляется в виде потока времени.
Метод расширения DR вне примера находит DR X , расширяя диффузное отображение 𝔉 на X .В большинстве случаев можно предположить, что новый набор данных Z имеет те же функции, что и X . Поэтому вместо повторного обучения всего набора X мы реализуем DR X , расширяя отображение 𝔉 только с X до X .
Во многих статьях представлены различные нестандартные алгоритмы расширения (см. [14, 18, 19] и ссылки на них). Однако математический анализ нестандартного расширения изучен недостаточно.
Основная цель этой статьи — дать математический анализ расширения DR вне выборки Dmaps. В Wang [20] мы предварительно изучили вневыборочные расширения DR для ядра PCA. Поскольку структура ядер для Dmaps отличается от ядра PCA, это требует специального анализа. В этой статье мы имеем дело с DR-расширениями Dmaps в рамках воспроизводящего гильбертова пространства ядра (RKHS), в котором расширение Dmaps можно классифицировать как расширение наименьших квадратов.
Статья организована следующим образом. В разделе 2 мы представляем общие расширения, не входящие в выборку, в структуре RKHS.В разделе 3 мы устанавливаем расширения DR Dmaps вне выборки методом наименьших квадратов. В разделе 4 мы даем математический анализ и алгоритмы расширения Dmaps DR. В последнем разделе мы приводим несколько примеров расширения.
2. Предварительная
Сначала введем некоторые понятия и обозначения. Пусть μ — конечная (положительная) мера на наборе данных X ⊂ ℝ D . Мы обозначили L 2 ( X , μ) (реальное) гильбертово пространство на X , снабженное внутренним произведением
. 〈F, g〉 L2 (X, μ) = ∫Xf (x) g (x) dμ (x), f, g∈L2 (X, μ).Тогда || f || L2 (X, μ) = 〈f, f〉 L2 (X, μ). Позже мы будем сокращать L 2 ( X , μ) до L 2 ( X ) (или L 2 ), если мера μ (и набор X ) не подвергается стрессу.
Определение 1 Функция k : X 2 → ℝ называется ядром Мерсера, если она удовлетворяет следующим условиям:
1. k симметрично: k ( x, y ) = k ( y, x ) ;
2. k — положительно полуопределенный;
3. k ограничено X 2 , то есть существует M > 0 такое, что | k ( x, y ) | ≤ M , ( x, y ) ∈ X 2 .
В этой статье мы рассматриваем только ядра Mercer. Следовательно, термин ядро будет обозначать ядро Мерсера. Расстояние ядра (связанное с k ) между двумя точками x, y ∈ X определяется как
dk (x, y) = k (x, x) + k (y, y) -2k (x, y).Ядро k определяет RKHS H k , в котором внутренний продукт удовлетворяет [21]
〈F (·), k (x, ·)〉 Hk = f (x), f∈Hk, x∈X. (1)Позже мы будем использовать H вместо H k , если ядро k не нагружено. Напомним, что k имеет двойную идентичность. Он выводит оператор идентификации на H , как показано в 1, а также выводит следующий компактный оператор K на L 2 ( X ):
(Kf) (x) = 〈f (·), k (x, ·)〉 L2 = ∫Xk (x, y) f (y) dμ (y), f∈L2.В [20] мы доказали, что если
k (x, y) = ∑j = 1mϕj (x) ϕj (y),, где набор {ϕ 1 , …, ϕ m } линейно независим, тогда набор является о.н. основа H . Следовательно, для f, g ∈ H с f = ∑jcjϕj и g = ∑jdjϕj имеем 〈f, g〉 Hk = ∑jcjdj.
Пусть спектральное разложение k будет следующим:
k (x, y) = ∑j = 1mλjvj (x) vj (y), 0≤m≤∞, (2), где собственные значения расположены по убыванию, λ 1 ≥ ··· ≥ λ m > 0, а собственные функции v 1 , v 1 , …, v м , нормализованы для удовлетворения
Запишите γi (x) = λivi (x).Тогда {γ 1 , …, γ m } является о.н. базис H , который называется каноническим базисом H . Мы также называем k (x, y) = ∑j = 1mγj (x) γj (y) каноническим разложением из k . К 2 имеем
γj = 1λj∫Xk (x, y) γj (y) dμ (y).Таким образом, если f ∈ H имеет каноническое представление f = ∑j = 1mcjγj, то для любого g ∈ H внутренний продукт 〈 f, g 〉 H имеет следующая интегральная форма:
〈F, g〉 H = ∑j = 1mcjλj∫Xg (x) γj (x) dμ (x).Чтобы исследовать расширение DR вне выборки, мы сначала напомним некоторые общие результаты о расширениях функций. Пусть X = X ∪ Z . Чтобы подчеркнуть, что точка x ∈ X также находится в X , мы используем x вместо x . Точно так же мы обозначаем k ( x, y ) ограничение k ( x, y ) на X 2 . То есть
k (x, y) = k (x, y), (x, y) ∈X2.Мы также обозначаем H RKHS, связанный с k .∈Af по методу наименьших квадратов из f , если
Очевидно, что расширение функции по методу наименьших квадратов единственно. Обозначим через T : H → H оператор продолжения по методу наименьших квадратов.
В Wang [20] мы уже доказали следующее:
1. Пусть { v 1 , …, v d } будет каноническим основанием для H и σ 1 ≥ σ 2 ≥ ··· ≥ σ d > 0 — собственные значения ядра k ( x, y ).d (X)] T обеспечивает расширение DR вне выборки методом наименьших квадратов на X .
3. Расширения DR вне выборки методом наименьших квадратов для Dmaps
Ядра Dmaps построены на основе гауссова ядра
ш (х, у) = ехр (- || х-у || 2ϵ), (х, у) ∈X2, ϵ> 0.Функция
определяет массовую плотность на X , а M = ∫XS (x) dμ (x) — это общая масса X .
Существуют две важные формы ядер Dmaps: диффузионное ядро Graph-Laplacian и ядро Laplace-Beltrami .
3.1. Dmaps с ядром графа-лапласиана
Сначала мы обсудим расширения DR вне выборки методом наименьших квадратов для Dmaps с ядром Graph-Laplacian (GL). Нормализуя ядро Гаусса на S ( x ), мы получаем следующее графо-лапласовское диффузионное ядро [4, 13]:
Это ядро относится к набору данных X , снабженному неориентированным (взвешенным) графом. Известно, что 1 является наибольшим собственным значением g ( x, y ), а соответствующая ему нормализованная собственная функция — S (x) M.
Пусть H g будет RKHS, связанным с ядром g и {ϕ 0 , ···, ϕ m } быть его каноническим основанием, что предполагает следующее спектральное разложение г ( х, г):
g (x, y) = ∑j = 0mλjvj (x) vj (y),, где 1 = λ 0 ≥ λ 1 ≥ ··· ≥ λ m > 0 и vj (x) = ϕj (x) / λj. Поскольку ϕ0 = S (x) M предоставляет только массовую информацию набора данных, он не должен находиться в пространстве признаков.Следовательно, мы определяем пространство признаков как RKHS, ассоциированное с ядром ∑j = 1mϕj (x) ϕj (y), где ϕ 0 удаляется.
Определение 2 . Отображение Φ: X → ℝm: Φ (x) = [ϕ1 (x), ···, ϕm (x)] T называется диффузионным отображением, а набор данных Φ ( X ) ⊂ ℝ м называется DR X .
Замечание . В Wang [20] мы уже указывали, что каждое ортогональное преобразование множества Φ ( X ) также можно рассматривать как DR X .Следовательно, любой неканонический o.n. Основа пространства признаков также обеспечивает отображение DR.
Чтобы изучить расширение вне выборки, как это было сделано в предыдущем разделе, мы принимаем X = X ∪ Z и обозначаем g ( x, y ) График-Лапласиан. ядро на X , то есть
, где S ( x ) — массовая плотность на X и
w (x, y) = w (x, y), (x, y) ∈X2,Предположим, что спектральное разложение g дается
g (x, y) = ∑j = 0dσjvj (x) vj (y).(4)Тогда RKHS H g , связанный с g , имеет каноническое основание {φ 0 , φ 1 , ···, φ d }:
g (x, y) = ∑j = 0dφj (x) φj (y),где φj = σjvj. Потому что S ( x ) ≠ S ( x ), в общем,
g (x, y) ≠ g (x, y), (x, y) ∈X2.Следовательно, мы не можем напрямую применить технику наращивания, описанную в предыдущем разделе, к g . Наша основная цель в этом подразделе — представить расширение с H g до H g .
Обозначим H w и H w RKHS, связанные с ядрами w и w , соответственно. Поскольку w ( x, y ) = w ( x, y ) для ( x, y ) ∈ X 2 , можно применить технику расширения, описанную в предыдущем разделе.
Пусть uj (x) = S (x) φj (x) и uj (x) = S (x) ϕj (x). Тогда у нас
w (x, y) = ∑j = 0duj (x) uj (y), w (x, y) = ∑j = 0muj (x) uj (y).Лемма 3 Оператор расширения наименьших квадратов T : H w → H w имеет следующее представление:
T (uj) (x) = 1σj∫Xw (x, y) uj (y) S (y) dμ (y), j = 0,1, ···, d. (5)Доказательство . Поскольку {uj} j = 0d не является каноническим мнением. основание H w , мы не можем напрямую применить формулу расширения 3. Напомним, что формулу 3 можно также записать как T ( f ) ( x ) = 〈 f , k ( x , ·)〉 H .(В рассматриваемом случае ядро w заменяет k .) Отметим, что
〈Uj, w (x, ·)〉 Hw = uj (x) = S (x) φj (x) = S (x) 1σj∫Xg (x, y) φj (y) dμ (y) = 1σj∫Xw (x, y) uj (y) S (y) dμ (y),, что означает, что для любого f ∈ H w мы имеем
〈f, uj〉 Hw = 1σj∫Xf (y) uj (y) S (y) dμ (y
.


 info
info