Как сделать объемную цифру: Объемные цифры на День Рождения: схемы, уроки

Содержание

Видеоинструкция, как сделать объемную цифру для фотозоны

Пожаловаться

Обновлено 28 янв 2020

День рождения — особенный праздник не только для детей, но и для их родителей. Где купить вкусный торт, во что нарядить имененника и, конечно, как оформить фотозону — вот вопросы, которые задают себе все мамы незадолго до важной даты. С последним наш журнал может помочь!

Цифры своими руками — 110 фото красивых вариантов оформления яркими и классными цифрами

Каждый родитель мечтает сделать для своего ребенка самый незабываемый и волшебный праздник в году – день рождение. Ради одной лучезарной улыбки и смеха, мама с папой заказывают торты, шары и огромное количество украшения, зазывают гостей, и даже арендуют ресторан. Конечно, легче пригласить специалистов, которые любое помещение превратят в сказочную страну. Но это вряд ли можно назвать интересным времяпрепровождением в кругу семьи.

Факт того, что праздник организован своими руками, а также на него подобраны индивидуальные декорации, заставляют ребенка гордиться своими родителями.

Если ваша фантазия не склонна самостоятельно подготовить зал и украсить его, то направьте свой взгляд на популярный вид украшения – объемные цифры на день рождение. Их можно не только купить, но изготовить самостоятельно.

Содержимое обзора:

Подходящие виды материалов
Каркас
Бумажный вид
Цветы
Бахрома
Тканый вид
Съедобный торт
Фото цифр своими руками

Подходящие виды материалов

Распространенным составляющим поделки являются – мелкие пластмассовые или надувные шары, которые требуется закрепить на каркас.

К сожалению, шарики относятся к классическому способу изготовления цифр, и давно наскучили большинству людей. Рассмотрим 3 известных и интересных метода создания декорации: бумажная, тканная и съедобная цифра.

Также Вы можете посмотреть интересный урок на профильном сайте по созданию поделок или украшений своими руками, к примеру портал рукоделия https://tytpodelki.ru/ — предлагает огромный выбор авторских и эксклюзивных работ.

Каждый из них отличается креативностью и способом подачи. Например, из ткани прекрасно выходят бабочки, цветы, бантики, а из бумаги умельцы способны сотворить любой вид оригами. Совсем новый вид праздничных цифр – торт из печенья, пирожных или бисквита.

Самостоятельное и ручное творение всегда цениться больше заводского, поэтому вы не пожалеете о потраченных финансах и времени. Особенно, если узнаете, что фигурку можно продать по привлекательной цене. Стоимость зависит от формы, размера и материала.

Каркас

Основой такой поделки является внутренняя крепкая конструкция, которая обеспечивает стойкость, позволяя сооружать на себя любую оболочку.

Наилучшим вариантом считается картон, крепящийся за счет клея, лески, скотча или скрепок. Он не будет валиться на бок или разваливаться по частям, если сделать цифры с пошаговой инструкцией.

Совсем мелкую форму можно распечатать самостоятельно, скачав наброски через интернет. Но ведь намного интереснее придать заготовке большой размер, например, метр или 2 от пола.

План по созданию каркаса 1-1.5 метра:

Существует 2 пути начального этапа: при помощи принтера заготовить выкройку или вручную нарисовать необходимую форму декорации.

Вырезаем и склеиваем все части между собой, не оставляем просветов, или соединяем скотчем.
Готовый шаблон прикладываем к картонке и вырезаем 2 одинаковые цифры.
Для объемной фигуры требуется изготовить еще соединительные части из требуемого материала.
Логично собираем все части воедино.

Каркас готов, осталось сделать цифры своими руками (если ребенку меньше 10, то 1 фигуру) и придать ей красивую внешность.

Бумажный вид

Данный тип декора требует определенных материалов: готовый каркас, ПВА клей, цветная бумага и активная фантазия.

Цветы

Наиболее простые и, одновременно, прекрасные фигурки из бумаги – это розочки или иные бутоны. Заранее заготавливаем цветные прочные салфетки, складываем 2-4 штуки вместе и формируем гармошку, которую обматываем тонкой ниткой посредине.

Осталось лишь распушить обе стороны салфеток, придавая им округлый вид, и приклеить на устойчивый каркас. Сложно сказать, какое количество бутонов потребуется.

Подключите фантазию или просмотрите видео-уроки по созданию других типов цветочной композиции. Лучшим вариантом служат пышные розы любого цвета.

Бахрома

Гофрированные цифры своими руками делать несложно, требуется лишь купить гофру нужных оттенков. Нарезанную ленту средней ширины и длины кладем в руку, немного растягивая один уголок, для получения эффекта волны.

Очень просто делаем из полоски красивый цветок: аккуратными движениями под наклоном скручиваем розочку вокруг заготовленного угла.

В конечном итоге должен появиться бутон на ножке. Крепим на каркасную основу розу при помощи клея, и оставляем в укромном месте сохнуть.

Тканый вид

Цифра из салфеток своими руками, конечно, заслуживает почетный пьедестал.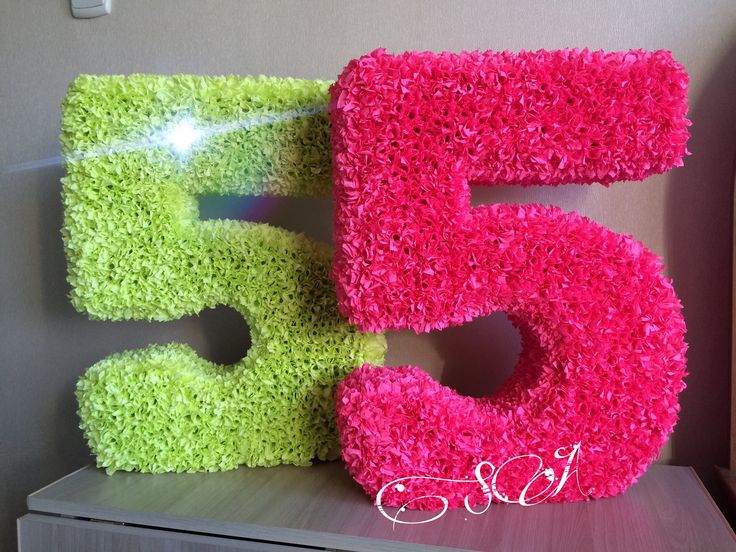 Но, если вы умелица, способная сотворить украшение из ткани, то данный способ для вас.

Начинающие рукодельницы также способны сотворить простой вариант декора – бантики.

План:

Желаемую ткань нарезаем на толстые и длинные прямоугольники.
Полоски скручиваем в банты или перевязываем ниткой (если ленты вышли короткими).
Банты крепим на каркас при помощи клеевого пистолета или клей-момента.

Необходимо располагать элементы очень туго, чтобы не просвечивался картон, а лучше окрасить его под нужный цвет. Яркая основа позволит изготовить малое количество бантиков.

Съедобный торт

Довольно новый способ поздравить именинника любого возраста – это подать ему торт с наступившим возрастом. Вам не обязательно уметь печь коржи, ведь за основу можно брать любые из этих ингредиентов:

Печенье – домашнее или купленное.
Фрукты, ягоды.
Маршмеллоу, зефир.
Вафли.
Готовые пирожные – будет очень удобно брать в руки.
Формы из мастики – любимые персонажи или традиционные фигуры.

Все ограничивается лишь полетом вашей фантазии. Популярное украшение стола понравиться не только детям, но и взрослым мужчинам, женщинам.

Сладость подойдет в качестве подарка начальнику, подруге, родителям, детям, коллегам. Торт цифра своими руками прекрасно дополнит картину любого праздничного застолья.

Помимо вышеперечисленных вариантов декораций существует еще масса способов продемонстрировать ваши умения, порадовать близких и неплохо заработать. Главное учитывать увлечения и половую принадлежность именинников.

Фото цифр своими руками

Горшки своими руками
Кораблик своими руками
Куклы своими руками
Серьги из бисера своими руками
Альбом своими руками
Коврики своими руками
Шторы своими руками
Букет из конфет своими руками
Колье из бисера своими руками
Кормушка своими руками
Как сшить резинку своими руками
Браслеты своими руками
Игрушки из фетра своими руками
Книга своими руками
Банты своими руками
Бабочки своими руками
Покрывало своими руками
Часы своими руками
Шкатулка своими руками
Топиарий своими руками
Панно своими руками
Блокнот своими руками
Подушка своими руками
Змей своими руками
Цветы из лент своими руками
Брошь из бисера своими руками
Коробка из картона своими руками
Чехол для телефона своими руками
Декор своими руками
Игрушки своими руками
Открытки своими руками
Бусины из бисера своими руками
Браслет из бисера своими руками
Домик из фанеры своими руками
Рамка своими руками
Конверт своими руками
Шары своими руками
Органайзер своими руками
Зеркало своими руками
Корзина для белья своими руками
Свадебные бокалы своими руками
Поделки из дисков своими руками
Украсить шампанское своими руками
Лизун своими руками
Ключница своими руками
Кашпо своими руками
Когтеточка своими руками
Футляр своими руками
Банты из атласных лент своими руками
Гирлянды из бумаги своими руками

Что такое объем? Значение, определение, формула, примеры, расчет

Что такое

Объем ?

Каждый трехмерный объект занимает некоторое пространство. Это пространство измеряется с точки зрения его объема. Объем определяется как пространство, занимаемое в границах объекта в трехмерном пространстве. Он также известен как мощность объекта.

Нахождение объема объекта может помочь нам определить объем, необходимый для заполнения этого объекта, например количество воды, необходимое для заполнения бутылки, аквариума или резервуара для воды.

Объем трехмерных фигур:

Поскольку разные трехмерные объекты имеют разную форму, их объемы также различны. Давайте посмотрим на некоторые трехмерные фигуры и научимся вычислять их объем (V).

Сфера

Самый простой и распространенный тип трехмерной формы — это сфера. Некоторые примеры сфер, которые мы видим в повседневной жизни, включают шары, глобусы, декоративные светильники, апельсины и т. д. Самое простое измерение, которое можно сделать на сфере, — это ее радиус. Объем сферы вычисляется по ее радиусу.

Объем сферы = $\frac{4}{3}$ πr ³ , где r — радиус сферы.

Куб

Следующая простая и распространенная трехмерная фигура — куб. Он определяется тем уникальным свойством, что каждая сторона куба имеет одинаковую длину. Некоторыми повседневными примерами предметов в форме куба являются игральные кости, кубики Рубика, кубики сахара, подарочные коробки и т. д. Объем куба рассчитывается по длине его стороны.

Объем куба = a ³ , , где a — длина каждой стороны куба.

Прямоугольная форма

Прямоугольная призма. В прямоугольном параллелепипеде длина сторон будет разной. Следующие обозначения используются для обозначения сторон прямоугольного параллелепипеда.

Длина = л
Ширина = b
Высота = ч

Все эти размеры используются для расчета объема прямоугольного параллелепипеда. Типичными примерами кубоидов являются книги, обувные коробки, кирпичи, матрацы и т. д.

Объем кубоида = l x b x h

Цилиндр

Цилиндр также представляет собой трехмерную форму с круглым основанием и высотой разделение двух оснований. К повседневным цилиндрическим предметам относятся бутылки с водой, ведра, свечи, банки и т. д. Объем цилиндра рассчитывается путем измерения радиуса основания и высоты.

Объем цилиндра = πr ² H , , где R — Radius базы, а H — это высота R — это Radius базовой и H — это высота R . .

Конус

Конус — это трехмерная форма, которую мы обычно видим вокруг себя. Рожок для мороженого, праздничная шляпа, воронка или рождественская елка — все это примеры конуса. Конус представляет собой характерную трехмерную геометрическую фигуру, которая имеет плоскую поверхность и криволинейную поверхность, направленную вверх.

Объем конуса = $\frac{1}{3}$πr ² h, где r — радиус основания конуса, а h — высота конуса из основание к вершине.

Измерение объема

Объем рассчитывается для трехмерных объектов и поэтому представляется в кубических единицах или в другом формате записи кубических единиц; так как это обычно используется (единица измерения)³, например, кубические сантиметры, кубический дюйм, кубический фут, кубический метр и т. д. Если длина или радиус измеряются в сантиметрах, то объем измеряется в кубических сантиметрах (см ³). Если размеры указаны в метрах, объем измеряется в кубических метрах (м ³ ).

Когда мы измеряем объем жидкости (например, чтобы найти объем воды, который может вместить цилиндрическая бутылка), мы должны изменить значения в см ³ или м ³ на литры. Объем можно перевести из литров в сантиметры по следующей формуле.

1 л = 1000 см ³

1 l = 1000 ml

1000 cm ³ = 1000 ml

So, 1 см ³ = 1 мл

Заключение

Понимание математических понятий, таких как объем, становится интересным с помощью наглядных пособий, таких как интерактивные игры. Вы можете проверить игры, рабочие листы и решенные задачи по темам, подобным этой, на веб-сайте Splashlearn. Посетите https://www.splashlearn.com/, чтобы узнать новые концепции, развлекаясь.

Решенные примеры

1. У Генри есть цилиндрическая бутылка для воды с радиусом основания 5 см и высотой 10 см. Какой объем воды может храниться в бутылке?

Решение:
Том бутылки = πr ² H

= π (5 x 5) x 10

= π x 250

= 3,14 x 250233333339

= 3,14 x 25023333333339

= 785 см ³

= 785 мл (1 см ³ = 1 мл)

2. Риаз владеет мячом для крикета радиусом 3 см. Какой объем занимает мяч в сумке Риаза?

Решение:
Объем шара = $\frac{4}{3}$ πr ³

= $\frac{4}{3}$ x $\frac{22 {7}$ x (3 x 3 x 3)

= 113,14 см ³

3. Коническая новогодняя елка изготовлена из глины. Высота дерева 14 дюймов, а диаметр основания 6 дюймов. Сколько глины используется? (используйте π = $\frac{22}{7}$)

Решение:

Диаметр = 6 дюймов

Радиус = $\frac{6}{2}$ = 3 дюйма

Объем глина = $\frac{1}{3}$ πr ² h

= $\frac{1}{3}\times \frac{22}{7}\times 3\times 3\times 14

= 132 кубических дюйма.

Практические задачи

l x l x l

b x b x b

h x h x h

l x b x h

Правильный ответ: l x b x h 9{3}$

Часто задаваемые вопросы

Является ли объем прямоугольной призмы таким же, как объем параллелепипеда?

Да, объем прямоугольной призмы такой же, как объем параллелепипеда. Кубоид имеет стороны неравной длины. Его объем рассчитывается по формуле л x b x h , где л, b и h — это различные измерения формы.

Как рассчитать объем неправильной формы?

Если вам нужно рассчитать объем фигуры, которая не является одной из правильных трехмерных фигур, разбейте неправильную форму на разные правильные формы. Добавьте отдельные объемы этих фигур, чтобы получить общий объем.

Как проще всего определить громкость?

Объем — это пространство, занимаемое любым объектом. Это занимаемое пространство зависит от формы объекта. Лучший способ понять — исследовать различные предметы и найти объем, занимаемый ими.

Что следует учитывать при расчете объемов различной формы?

Важной проверкой перед расчетом объема любой формы должно быть то, что все измерения должны быть в одних и тех же единицах измерения. Если одно измерение указано в см, а другое в м, перед расчетом объема конвертируйте оба значения в см или м.

Объем – формула, определение, расчет, примеры

Объем – это мера емкости, которую содержит объект. Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой. В этом можно убедиться с помощью простого упражнения дома:

Возьмите прямоугольный лист бумаги длиной ‘ l ‘ см и шириной ‘ h ‘ см.
Соедините противоположные стороны листа бумаги, не сгибая лист.
Вы создали трехмерный объект, заключающий внутри себя пространство, из двухмерного листа.

1.	Определение тома
2.	Объем трехмерных фигур
3.	Список формул объема
4.	Как рассчитать объем?
5.	единиц объема
6.	Калькулятор объема
7.	Часто задаваемые вопросы по тому

Определение тома

Объем определяется как объем, занимаемый трехмерной твердой формой. В любой форме это трудно визуализировать, но можно сравнить между формами. Например, объем ящика компаса больше объема помещенного в него ластика. Для вычисления площади любой двумерной фигуры мы делим часть на равные квадратные единицы. Точно так же при вычислении объема объемных фигур мы будем делить его на равные кубические единицы. Давайте узнаем, как рассчитать объем различных твердых фигур в нашем следующем разделе.

Объем 3D-фигур

Каждый предмет в нашем окружении имеет свойство занимать пространство. Эти реальные объекты можно легко сравнить с основными трехмерными формами. Давайте посмотрим на объем этих твердых фигур в деталях.

Объем кубоида

Предположим, у нас есть несколько прямоугольных листов длиной ‘l’ и шириной ‘ b’ . Если мы сложим их один поверх другого до высоты ‘h’ , мы получим прямоугольный параллелепипед размерности л, б, з . Это можно увидеть на следующем рисунке, на котором показаны длина, ширина (ширина) и высота образованного таким образом прямоугольного параллелепипеда.

Чтобы вычислить количество пространства, заключенного в этот прямоугольный параллелепипед, мы используем формулу: Объем кубоида = l × b × h

Объем куба

Куб является частным случаем параллелепипеда, где все три стороны равны по мере. Если мы представим это равное значение как «а», то объем этого куба можно будет рассчитать по формуле: Объем куба = а × а × а = а³. Обратите внимание на следующий рисунок, чтобы увидеть равные стороны куба и пространство, которое он занимает.

Объем цилиндра

Точно так же, как мы построили прямоугольный параллелепипед из прямоугольников, мы можем построить цилиндр из кругов того же размера.

Цилиндр представляет собой трубчатую конструкцию с двумя параллельными круглыми основаниями, соединенными изогнутой поверхностью на фиксированном расстоянии от центра. Расстояние между этими двумя основаниями и есть высота цилиндра. Если мы рассмотрим «r» как радиус круглого основания (и вершины), а «h» как высоту цилиндра, то объем цилиндра можно выразить как объем цилиндра = π r² h

Объем пирамиды

Пирамиды имеют многоугольник в качестве основания и треугольные грани, которые сходятся на вершине.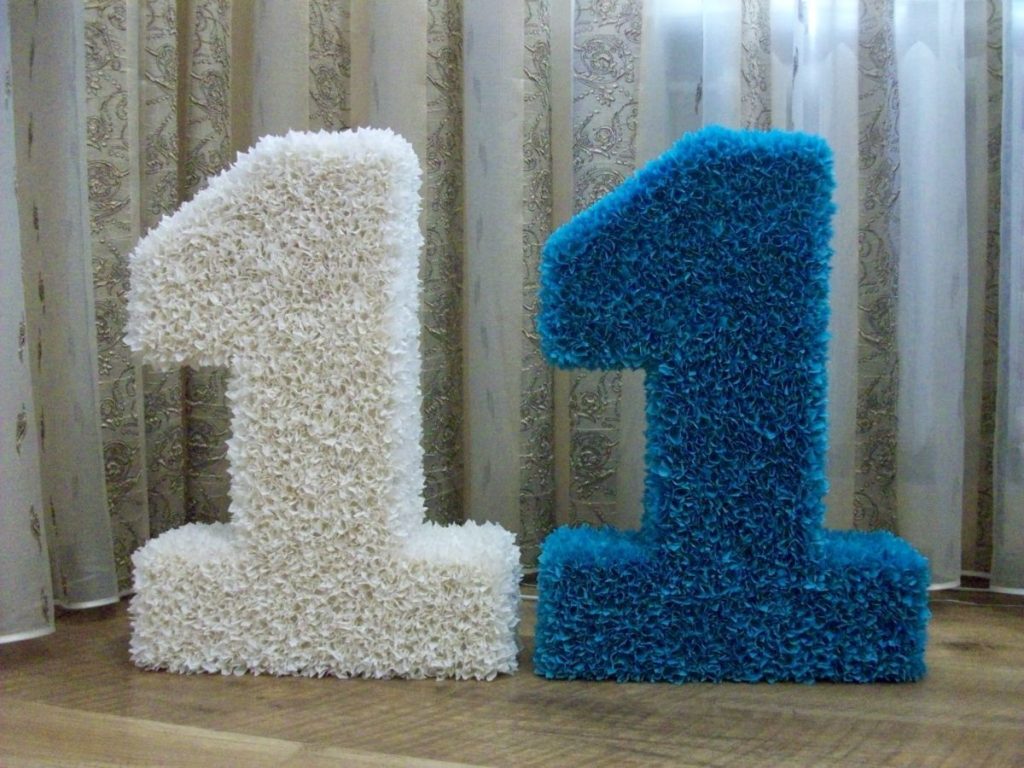 Объем пирамиды рассчитывается по формуле: Объем пирамиды = 1/3 × длина основания × ширина основания × высота пирамиды. Эту формулу также можно записать в виде 1/3 × площадь основания многоугольника × высота пирамиды.

Объем конуса

Разница между конусом и пирамидой в том, что основание конуса круглое, а основание пирамиды многоугольник. Объем конуса рассчитывается по формуле: 1/3 × πr ² ч.

Объем шара

Объем шара – это занимаемое им пространство.

Объем сферы, радиус которой r равен 4/3 πr³.

Теперь, когда мы знакомы с формулами различных геометрических фигур, давайте взглянем на различные единицы объема.

Список формул объема

Ниже приведен подробный табличный список формул объема в двух словах, описывающий формулы объема для всех возможных трехмерных (теловидных) форм.

Как рассчитать объем?

Вот шаги для расчета объема любой твердой формы:

Определите все заданные параметры, которые являются полезными и которые необходимо заменить в соответствующей формуле объема. Например, радиус должен быть «r», а высота — «h», наклонная высота, диаметр и т. д.
Убедитесь, что все параметры имеют одинаковые единицы измерения.
Подставьте значения в формулу объема соответствующих фигур.
Запишите единицы измерения в кубических единицах.

Давайте разберемся с шагами на примере.

Пример: Найдите объем прямоугольного цилиндра радиусом 25 м и высотой 1 метр. Используйте π = 3,142.

Решение:

Радиус цилиндра r = 25 м.
Его высота h = 1 метр.
Объем цилиндра V = πr ² h = (3,142)(25) ² (1) = 1963,75 м ³ .
Объем баллона 1963,75 куб.м.

Единицы объема

Единицей объема в системе СИ является кубический метр (м ³ ), поскольку объем представляет собой количество трехмерного пространства, занимаемого формой или поверхностью. Однако наиболее часто используемой единицей измерения объема является литр. Кроме того, большие и малые объемы измеряются в других единицах, таких как миллилитры (мл), пинты, галлоны и другие. В следующей таблице показаны несколько единиц, связанных с объемом, и их метрические эквиваленты.

Боковой блок	Единица объема	Метрический эквивалент
Дюйм	кубических дюймов (в ³ )	1 куб. дюйм = 16,387064 мл
Ножка	кубических футов (³ футов)	1 куб.фут = 28,316846592 л
см	Кубический сантиметр (см ³ )	1 кубический сантиметр = 1 мл
Двор	Кубический ярд (ярд ³ )	1 куб.ярд = 764,554857984 л 1 куб.ярд = 0,764554857984 м ³

В то время как стандартной единицей измерения в США является кубический ярд или кубический дюйм, более широко используемыми единицами измерения являются галлоны, пинты или жидкие унции. В следующей таблице показаны некоторые из этих единиц и их эквивалентные метрические преобразования.

Блок	Эквивалентное преобразование
1 пинта (pt)	2 чашки
1 кварта (кварт)	2 балла
1 галлон	3,78 литра
1 литр	1000 кубических сантиметров

Калькулятор объема

Калькулятор объема помогает быстро и легко рассчитать объем любой заданной формы. Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.

☛Также проверьте:

Калькулятор объема цилиндра
Калькулятор объема сферы
Калькулятор объема куба
Калькулятор объема прямоугольного параллелепипеда

☛Статьи по теме

Ознакомьтесь со статьями, посвященными объему различных объемных форм.

Объем конуса
Объем цилиндра
Объем прямоугольного параллелепипеда
Том Пирамиды

Примеры томов

Пример 1: У Эдвина есть конический сосуд радиусом 6 дюймов и высотой 7 дюймов. Каков объем сосуда? Используйте π = 22/7.
Раствор.
Сосуд имеет форму конуса.
Объем конуса = 1/3 π r² h = 1/3 × 22/7 × 6 × 6 × 7 = 264 дюйма³
∴ Объем судна 264 куб. дюйм
Пример 2: Джо любит играть со строительными блоками. Он построил конструкцию из 15 кубов. Если длина (ребро) каждого куба равна 3 дюймам, каков будет объем его конструкции?
Раствор.
Рассчитаем объем одного куба. Объем куба = ребро × ребро × ребро = 3 × 3 × 3 = 27 дюймов³
В его структуре 15 кубиков. Итак, объем всей конструкции:
Объем конструкции = 15 × объем одного куба = 15 × 27 = 405 дюймов³
∴ Объем конструкции 405 дюймов³.
Пример 3: Если диаметр мяча 14 дюймов, сколько воздуха может вместить мяч? Используйте π = 3,14
Решение.
Количество воздуха внутри шара займет все пространство в шаре. Итак, нам нужно найти объем шара.
Радиус шара 14/2 дюйма = 7 дюймов
Объем шара = 4/3 πr³
= [4/3 × 3,14 × (7)³]
= 1436,02 дюйма³
∴ Мяч содержит 1436,02 дюйма³ воздуха.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по объему

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о томе

Что означает объем?

Объем — это мера емкости, которую содержит объект. Скажем, если чашка может вместить 1000 мл сока, говорят, что ее объем равен 1000 мл. В этом случае объем также можно определить как количество сока, занимаемое чашкой. Объем всегда рассчитывается путем деления емкости фигур на равные кубические единицы.

☛Загрузите прямо сейчас, чтобы попрактиковаться.

Объемные листы
Объем кубов Рабочие листы
Рабочий лист «Объем конуса»
Объем цилиндра Рабочие листы

Какова формула объема частичного конуса?

Объем частичного конуса можно рассчитать по формуле: V = 1/3 × πh(R² + Rr + r²), где «R» — радиус основания конуса, а «r» — радиус верхней поверхности.

☛ Прочтите основы здесь:

Объем правого кругового конуса
Объем частичного конуса
Объем конуса в единицах числа Пи

Как найти объем пирамид?

Объем пирамиды рассчитывается по формуле: V = 1/3 × Площадь основания × Высота.

☛ Также проверьте:

Объем прямоугольной пирамиды
Объем треугольной пирамиды
Объем прямоугольной пирамиды

Как найти объем конуса?

Объем конуса составляет 1/3 объема цилиндра той же высоты и того же основания. Формула, используемая для нахождения объема конуса: 1/3 × π r² h; где «r» — радиус, а «h» — высота конуса.

Как найти объем цилиндра?

Объем цилиндра рассчитывается по формуле: V = площадь основания цилиндра × высота, а также представляется как объем цилиндра = π r² h; где «r» — радиус цилиндра, а «h» — высота.

В чем разница между объемом и площадью?

Объем фигуры или твердого тела — это пространство, занимаемое им, которое также включает его высоту или глубину. Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.

☛ Проверьте список важных математических формул:

Формулы площади
Формулы площади поверхности
Геометрические формулы
Формулы измерения

Каков объем мяча?

Поскольку шар является сферой, его объем будет рассчитан по формуле объема сферы. Формула объема сферы: 4/3 πr³, где «r» — радиус сферы.

Какая формула объема цилиндра?

Формула объема цилиндра = πr²h; где «r» — радиус основания цилиндра, а «h» — высота.

Как найти объем призмы?

Мы можем найти объем призмы, записав заданные размеры призмы. Затем подставьте значения в формулу объема V = B × H, где «V», «B» и «H» — это объем, площадь основания и высота призмы. Получив значение объема призмы, в конце запишите единицу объема призмы (в кубических единицах).

☛Чек:

Объем призмы
Объем призм с заданиями

Как найти объем бака?

Объем резервуара зависит от его формы. В зависимости от размера мы можем использовать приведенные ниже формулы:

Объем параллелепипеда = l × b × h; где «l» — длина прямоугольного параллелепипеда, «b» — ширина (ширина) прямоугольного параллелепипеда, а «h» — высота прямоугольного параллелепипеда.
Объем куба = a ³ , где «a» — ребро куба.