схемы оригами из бумаги. Как сделать объемный куб пошагово? Простая поэтапная схема складывания пирамиды
Техника оригами дает возможность своими руками изготавливать самые разные оригинальные поделки из бумаги. Необычно будут смотреться декоративные изделия в виде геометрических фигур.
Как сделать куб?
Для начала мы рассмотрим, как можно поэтапно создать поделку в форме куба. Данная фигура считается несложным многогранником. В ней сразу все грани будут квадратными. Рисунок развертки можно просто распечатать при помощи принтера. Также можно начертить ее самостоятельно.
В последнем случае сначала необходимо определиться с размерами граней. При этом ширина бумажного листа должна составлять не менее трех сторон такого квадрата, а длина – не более пяти сторон. Во всю длину бумажного листа чертят 4 квадрата, они позже станут боковыми частями куба. Прорисовывать все надо только вплотную и на одной полосе. После этого и под, и над одним из квадратов чертят еще по одной квадратной фигуре.
Позже рисуют полосы для приклеивания. Это позволит легко соединить грани друг с другом. На заключительном этапе изготовления нужно будет хорошо промазать места соединений клеевым составом.
Данные части склеиваются друг с другом и ненадолго закрепляются при помощи скрепок, чтобы вещество успело высохнуть. Так фиксируют все грани куба.
Создание пирамиды
Далее мы разберем, как легко сделать фигуру в форме пирамиды. Данная фигура представляет собой многогранник, в котором основанием является многоугольник, а все остальные грани имеют вид треугольников с одной вершиной.
Данная фигура представляет собой многогранник, в котором основанием является многоугольник, а все остальные грани имеют вид треугольников с одной вершиной.- Сначала следует точно выбрать все размеры, а также количество граней фигуры.
- После этого на бумажном листе при помощи карандаша чертят основание в виде многоугольника. В зависимости от общего количества граней основание может быть сделано в виде пятиугольной, квадратной или треугольной заготовки.
- Затем из одной из сторон полученного многоугольника следует сделать треугольник,
- Позже прорисовывают еще один треугольник. При этом одна из его сторон должна быть общей с первой фигурой. Всего их рисуется столько, сколько в итоге будет частей в пирамиде.
- Далее отмечают полоски для приклеивания. На заключительном этапе нарисованную фигуру аккуратно вырезают и склеивают по намеченным линиям.

Складывание других фигур
Разберем, как пошагово сложить другие объемные фигуры в технике оригами.
Цилиндр
Он представляет собой фигуру, которая ограничивается цилиндрической поверхностью и плоскостями, пересекающими ее и располагающимися параллельно. На первом этапе на материале отмечают прямоугольник, при этом его ширина будет являться высотой изделия, а длина – диаметром. Далее дорисовывают небольшие треугольники для склеивания. После этого на материале чертят два круга, их диаметр должен равняться диаметру готового цилиндра. Эти круги станут верхним и нижним основанием фигуры. Все детали вырезаются ножницами, боковая часть изделия склеивается из прямоугольной заготовки.
Все элементы должны полностью просохнуть. Далее к ним также фиксируют нижнее и верхнее основание.
Параллелепипед
Отдельно прорисовываются места, предназначенные для приклеивания.
Далее полученная схема вырезается и склеивается по отмеченным полоскам.
Призма
Чтобы сделать треугольную призму, на материале чертят три прямоугольника с одинаковыми размерами. После этого над и под прямоугольником, который размещается в центральной части, рисуют по одному небольшому треугольнику. Они также должны иметь одинаковые размеры. После этого со всех сторон оставляют небольшие полоски. Оставленные полоски промазываются клеевым составом, затем все части фиксируются друг с другом, формируя при этом объемную треугольную призму.В технике оригами также можно сделать шестиугольную призму. В данном случае на бумажном листе чертят 6 прямоугольников с одинаковыми длиной и шириной.
Вместо треугольников сверху и снизу прорисовывают шестиугольные фигуры.
В конце также оставляют полосы для склеивания, все это вырезается и склеивается в одно изделие.
О том, как сделать куб в технике оригами, смотрите в следующем видео.
Четырехугольник из бумаги схема — hohjieque.jnario.org
Четырехугольник из бумаги схема
Сборник психологических игр. Первая часть сборника включает игры – «энерджайзеры», направленные на создание благоприятной атмосферы Изготовление обыкновенного кубика из бумаги — несложная затея, и, научившись этому искусству, вы сможете изготавливать композиции разной сложности без всякого труда.
 Можно распечатать схемы из интернета, потом нанести их на плотную бумагу, не забывая про линии сгиба Объемные геометрические фигуры вполне с лгкостью можно сделать из бумаги либо из картона. При этом вы сами можете выбрать цветовое решение вашей объмной фигуры. Примечание. Высоты сечения рельефа, значения которых отмечены звездочкой, на топографических планах населенных пунктов не применяются. Снежинка из бумаги. Перед тем, как сделать снежинку, из бумаги нужно сложить простую заготовку, на которую в дальнейшем и будет наноситься схема для вырезания. Развертки из бумаги или картона изготовить непросто. Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами. Пояснительная записка Основные задачи модернизации российского образования — повышение его доступности, качества и эффективности.
Невероятно красивые цветы из бумаги в технике оригами. Подарите себе и детям весеннее настроение.
Можно распечатать схемы из интернета, потом нанести их на плотную бумагу, не забывая про линии сгиба Объемные геометрические фигуры вполне с лгкостью можно сделать из бумаги либо из картона. При этом вы сами можете выбрать цветовое решение вашей объмной фигуры. Примечание. Высоты сечения рельефа, значения которых отмечены звездочкой, на топографических планах населенных пунктов не применяются. Снежинка из бумаги. Перед тем, как сделать снежинку, из бумаги нужно сложить простую заготовку, на которую в дальнейшем и будет наноситься схема для вырезания. Развертки из бумаги или картона изготовить непросто. Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами. Пояснительная записка Основные задачи модернизации российского образования — повышение его доступности, качества и эффективности.
Невероятно красивые цветы из бумаги в технике оригами. Подарите себе и детям весеннее настроение.
 Многим школьникам сложно осмыслить это понятие и тем. Для кабельных линий, находящихся в эксплуатации более 15 лет, перегрузки должны быть понижены #5 Поделки из бумаги на Новый год: делаем рождественский венок своими руками. Раз уж речь пошла о декоре квартиры, странно было бы не упомянуть рождественские или как их еще называют новогодние венки. Бумажные и картонные поделки/Бумага Детское творчество/Поделки из Бумаги и картона Шаблоны. Метки: геометрия фигуры из бумаги шаблоны детское творчество занятие развитие. Процитировано 11 раз Понравилось: 3 пользователям.
24. Выпуклые четырехугольники. ЧЕТЫРЕХУГОЛЬНИККаждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали.Две несмежные стороны называются Нарисовать Прямоугольник от руки не так уж и сложно, как это может показаться поначалу. Параллелогра́мм — это четырехугольник, у которого противоположные стороны параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Многим школьникам сложно осмыслить это понятие и тем. Для кабельных линий, находящихся в эксплуатации более 15 лет, перегрузки должны быть понижены #5 Поделки из бумаги на Новый год: делаем рождественский венок своими руками. Раз уж речь пошла о декоре квартиры, странно было бы не упомянуть рождественские или как их еще называют новогодние венки. Бумажные и картонные поделки/Бумага Детское творчество/Поделки из Бумаги и картона Шаблоны. Метки: геометрия фигуры из бумаги шаблоны детское творчество занятие развитие. Процитировано 11 раз Понравилось: 3 пользователям.
24. Выпуклые четырехугольники. ЧЕТЫРЕХУГОЛЬНИККаждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали.Две несмежные стороны называются Нарисовать Прямоугольник от руки не так уж и сложно, как это может показаться поначалу. Параллелогра́мм — это четырехугольник, у которого противоположные стороны параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Параллелограмм — плоская фигура. На Студопедии вы можете прочитать про: Схема четырехугольника. Схема многоугольника обладает наибольшей устойчивостью в аварийных ситуациях типа «отказ». Отказ любого присоединения или элемента данной схемы отключается двумя выключателями (в том числе. Как сделать объемные поделки из бумаги.Оригами из треугольных модулей. Модульное оригами представляет собой удивительную технику создания фигурок из бумаги с помощью нескольких Очень часто встречаются схемы оригами, использующие треугольные модули.
Танграм можно сделать из картона или бумаги, распечатав шаблон и разрезав по линиям. Схемы и фигуры игры танграм. В последнее время танграм частенько используют дизайнеры. Самое удачное применение танграма, пожалуй, в качестве мебели. Если это видео наберёт 10 лайков то вы увидите мой новый мастер-класс. 2. Приступим к начертанию схемы прямоугольного параллелепипеда на бумаге. Аналогичным методом построим нижний прямоугольник на противоположной стороне. 6. Для того, чтобы было легче склеивать параллелепипед из бумаги, добавим к чертежу дополнительные.
Параллелограмм — плоская фигура. На Студопедии вы можете прочитать про: Схема четырехугольника. Схема многоугольника обладает наибольшей устойчивостью в аварийных ситуациях типа «отказ». Отказ любого присоединения или элемента данной схемы отключается двумя выключателями (в том числе. Как сделать объемные поделки из бумаги.Оригами из треугольных модулей. Модульное оригами представляет собой удивительную технику создания фигурок из бумаги с помощью нескольких Очень часто встречаются схемы оригами, использующие треугольные модули.
Танграм можно сделать из картона или бумаги, распечатав шаблон и разрезав по линиям. Схемы и фигуры игры танграм. В последнее время танграм частенько используют дизайнеры. Самое удачное применение танграма, пожалуй, в качестве мебели. Если это видео наберёт 10 лайков то вы увидите мой новый мастер-класс. 2. Приступим к начертанию схемы прямоугольного параллелепипеда на бумаге. Аналогичным методом построим нижний прямоугольник на противоположной стороне. 6. Для того, чтобы было легче склеивать параллелепипед из бумаги, добавим к чертежу дополнительные. Как сделать параллелепипед из бумаги. Как сделать параллелепипед из белой бумаги. На второй и третьей вертикальных прямых отметьте от их начала и конца (вверх и вниз) по 5 см, так как у нас ширина одной стороны 5 см и соедините концы отрезков, получив четырехугольник. В этом уроке мы покажем вам как ребенку сделать параллелепипед из бумаги своими руками поэтапно, всего за 7 простых шагов. Для начала потребуется выбрать подходящую бумагу. Если вы просто хотите научиться делать параллелепипед своими руками, то можете взять. Эти недостатки привели к использованию РУ, имеющих схемы в виде многоугольников. Стороны многоугольников образуются выключателями, а к вершинам подводятся присоединения, число которых равно числу вершин. Число выключателей в многоугольниках равно числу. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху. Развёртка шара из бумаги представляет собой дольки, полоски бумаги сужающиеся по краям. Развёртка шара похожа на рисунок из полосок на арбузе.
Как сделать параллелепипед из бумаги. Как сделать параллелепипед из белой бумаги. На второй и третьей вертикальных прямых отметьте от их начала и конца (вверх и вниз) по 5 см, так как у нас ширина одной стороны 5 см и соедините концы отрезков, получив четырехугольник. В этом уроке мы покажем вам как ребенку сделать параллелепипед из бумаги своими руками поэтапно, всего за 7 простых шагов. Для начала потребуется выбрать подходящую бумагу. Если вы просто хотите научиться делать параллелепипед своими руками, то можете взять. Эти недостатки привели к использованию РУ, имеющих схемы в виде многоугольников. Стороны многоугольников образуются выключателями, а к вершинам подводятся присоединения, число которых равно числу вершин. Число выключателей в многоугольниках равно числу. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху. Развёртка шара из бумаги представляет собой дольки, полоски бумаги сужающиеся по краям. Развёртка шара похожа на рисунок из полосок на арбузе. Затем следует вырезать из бумаги развертку тетраэдра и склеить. Если найдется 4 листа разноцветной бумаги, то тетраэдр получится ещё красивее. Правильная пирамида — это разновидность пирамид, у которой в основании лежит правильный четырехугольник — квадрат. Как научиться делать объемные фигуры из бумаги и картона? Яркие объемные поделки из бумаги привлекут внимание ребенка и уж точно не дадут скучать. А Вы незаметно и с задором проведете горячо любимое чадо в мир занимательной геометрии. Возьмите заготовленный лист бумаги и начертите параллелепипед в развернутом виде. Для подсказки воспользуйтесь схемой. Как видите, на рисунке шесть ключевых прямоугольников, условно поделенных на три пары абсолютно одинаковых по размеру фигур (пары А-размера. Из цветной бумаги вырезать части головоломки. Пример схемы собаки — сделали ученики 1 класса к уроку математики и технологии. Схема — ракета. Так можно сложить из танграма домик. На втором этапе можно предложить детям выложить фигуры по сплошному рисунку.
Затем следует вырезать из бумаги развертку тетраэдра и склеить. Если найдется 4 листа разноцветной бумаги, то тетраэдр получится ещё красивее. Правильная пирамида — это разновидность пирамид, у которой в основании лежит правильный четырехугольник — квадрат. Как научиться делать объемные фигуры из бумаги и картона? Яркие объемные поделки из бумаги привлекут внимание ребенка и уж точно не дадут скучать. А Вы незаметно и с задором проведете горячо любимое чадо в мир занимательной геометрии. Возьмите заготовленный лист бумаги и начертите параллелепипед в развернутом виде. Для подсказки воспользуйтесь схемой. Как видите, на рисунке шесть ключевых прямоугольников, условно поделенных на три пары абсолютно одинаковых по размеру фигур (пары А-размера. Из цветной бумаги вырезать части головоломки. Пример схемы собаки — сделали ученики 1 класса к уроку математики и технологии. Схема — ракета. Так можно сложить из танграма домик. На втором этапе можно предложить детям выложить фигуры по сплошному рисунку. Таблица — многогранники, которые можно изготовить своими руками из бумаги, даны ссылки на инструкции, схемы, развертки в различных источниках (чтобы увидеть примерный внешний вид готовой Ссылки на инструкции, схемы, развертки многогранников из бумаги. Веннинджер.
Мастер-класс Поделка изделие Оригами Правильный шестиугольник из квадрата Бумага. Поделиться. Четырехугольник — схема, таблица. Скачать структурно-логическую схему бесплатно. Четырехугольник — структурно-логическая схема. Источник. Ваш ребенок учится в школе? Плохо разбирается в геометрических фигурах и не имеет пространственного мышления? Тогда предлагаем мастер-класс для совместной работы, который покажет, как сделать объемную модель параллелепипеда из бумаги.
Рабочая программа по математике. Пояснительная записка. Рабочая программа по учебному. Программа предшкольной подготовки является программой одного из курсов по внеурочной. Сборник психологических игр. Первая часть сборника включает игры – энерджайзеры.
cкачать: АООП НОО для детей с РАС Вариант.
Таблица — многогранники, которые можно изготовить своими руками из бумаги, даны ссылки на инструкции, схемы, развертки в различных источниках (чтобы увидеть примерный внешний вид готовой Ссылки на инструкции, схемы, развертки многогранников из бумаги. Веннинджер.
Мастер-класс Поделка изделие Оригами Правильный шестиугольник из квадрата Бумага. Поделиться. Четырехугольник — схема, таблица. Скачать структурно-логическую схему бесплатно. Четырехугольник — структурно-логическая схема. Источник. Ваш ребенок учится в школе? Плохо разбирается в геометрических фигурах и не имеет пространственного мышления? Тогда предлагаем мастер-класс для совместной работы, который покажет, как сделать объемную модель параллелепипеда из бумаги.
Рабочая программа по математике. Пояснительная записка. Рабочая программа по учебному. Программа предшкольной подготовки является программой одного из курсов по внеурочной. Сборник психологических игр. Первая часть сборника включает игры – энерджайзеры.
cкачать: АООП НОО для детей с РАС Вариант. Скачать ГКИНП 02-033-82: Инструкция по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500. ДОПУСТИМЫЕ ДЛИТЕЛЬНЫЕ ТОКИ ДЛЯ ПРОВОДОВ, ШНУРОВ И КАБЕЛЕЙ С РЕЗИНОВОЙ ИЛИ ПЛАСТМАССОВОЙ. ПРАВИЛА УСТРОЙСТВА ЭЛЕКТРОУСТАНОВОК (ПУЭ) (ШЕСТОЕ ИЗДАНИЕ, переработанное и дополненное Приказ Минобразования РФ от 05.03.2004 n 1089 Об утверждении федерального компонента. Читать онлайн — Татаринов Юрий Аркадьевич. Города Беларуси в некоторых интересных.
Григорий Климов. Имя мое легион—— Copyright Григорий.
Скачать ГКИНП 02-033-82: Инструкция по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500. ДОПУСТИМЫЕ ДЛИТЕЛЬНЫЕ ТОКИ ДЛЯ ПРОВОДОВ, ШНУРОВ И КАБЕЛЕЙ С РЕЗИНОВОЙ ИЛИ ПЛАСТМАССОВОЙ. ПРАВИЛА УСТРОЙСТВА ЭЛЕКТРОУСТАНОВОК (ПУЭ) (ШЕСТОЕ ИЗДАНИЕ, переработанное и дополненное Приказ Минобразования РФ от 05.03.2004 n 1089 Об утверждении федерального компонента. Читать онлайн — Татаринов Юрий Аркадьевич. Города Беларуси в некоторых интересных.
Григорий Климов. Имя мое легион—— Copyright Григорий.
Проектная деятельность на тему: «Математика и оригами. Ориганометрия»
Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа №27 г. Йошкар-Олы»
Исследовательская работа
Математика и оригами. Ориганометрия
Выполнил: Богданова Анна, Чулкова Юлия
ученицы 5в класса
Научный руководитель: Михайлова Т. Ю.
Ю.
учитель математики
Йошкар-Ола, 2016г.
Содержание
«В мире постоянны только перемены», – гласит буддийская мудрость, воплотившаяся в оригами.
Оригами – это древнее искусство складывания фигурок из бумаги. Искусство оригами своими корнями уходит в Древний Китай, где и была изобретена бумага. Первоначально оригами использовалось в религиозных обрядах. Долгое время этот вид искусства был доступен только представителям высших сословий, где признаком хорошего тона было владение техникой складывания из бумаги.
Увлекаясь искусством оригами, мы заметила, что складывая фигурки оригами, мы часто сталкиваюсь с математическими понятиями. И нам стало интересно, как связаны таинственное искусство складывания фигурок из бумаги и давно интересующая нас математика.
Цель: установить взаимосвязь искусства оригами и науки математики.
Задачи:
изучить источники информации по предмету исследования;
изучить историю оригами, основные этапы его развития;
рассмотреть базовые формы и приемы оригами;
исследовать связь математики и оригами;
заинтересовать окружающих таинственным искусством складывания фигурок.
провести мастер-класс для своих одноклассников
Основные результаты:
проводя исследования по данной теме, мы изучили азбуку и базовые формы оригами, смогли понять, как связаны математика и оригами, нашли аргументы и факты по выдвинутой гипотезе, сами делали оригами, провели исследование (опрос), сделали эксперимент и провели мастер-класс по оригами.
Практическая значимость:
наша работа показывает возможность использования искусства оригами на уроках математики.

данная тема представляет большие возможности для проявления исследовательских и творческих умений при решении задач.
Праздники – это часть нашей повседневной жизни, которые необходимы как еда, как сон, как труд. Не было бы праздников, наша жизнь была бы скучной и однообразной, согласитесь? У каждого человека есть хоть один любимый праздник, у кого-то это Новый год, Рожденство,23 февраля,8 марта, а у нас это день рождение, а у Вас какой?
Когда наступает день рождение, мы приглашаем к себе домой друзей. И, конечно же, хочется сделать так, чтобы праздник был необычным и надолго запоминающимся и нам, и нашим гостям. Своих друзей каждый раз хотим удивить не только вкусными угощениями, но и необычной, оригинальной сервировкой стола. Мы с нашими мамами постоянно сворачиваем салфетки для стола и для столовых приборов разными способами, а в этом нам помогает искусство оригами.
Благодаря искусству оригами мы радуем младших братьев и сестер. Делаем им-то самолетики, то кораблики, то разных зверушек из бумаги. И это все их в такой неописуемый восторг приводит.
Делаем им-то самолетики, то кораблики, то разных зверушек из бумаги. И это все их в такой неописуемый восторг приводит.
Думаем, многим нравится такой праздник как Новый год. Подготовку к нему некоторые начинают заранее. Мы в школе уже в начале декабря начинаем украшать кабинеты. Создаем эти украшения своими руками. И в этом опять нам помогает искусство оригами.
Помимо украшений, мы дарим, друг другу в классе открытки, которые складываем из бумаги. И тут опять помогает нам оригами.
Мы знаем, что оригами это искусство складывать всевозможные фигуры из бумаги. Бумажные фигурки умеют делать и дети, и взрослые. Оригами даже преподают в школах, о нем пишут книги и выпускают журналы с интересными статьями и описанием различных моделей. Мы заметили, что, складывая фигурки оригами, сталкиваемся с математическими понятиями. Нам стало интересно, как связаны искусство складывания фигурок из бумаги и давно интересующая нас математика. С таким вопросом мы подошли к нашей учительнице по математике Татьяне Юрьевне. И мы решили подробнее эту тему изучить.
С таким вопросом мы подошли к нашей учительнице по математике Татьяне Юрьевне. И мы решили подробнее эту тему изучить.
Гипотеза: Искусство оригами тесно связано с математикой и может стать хорошей основой для ее изучения
Объект исследования – связь математики и оригами.
Предмет исследования – фигуры геометрические и оригами.
Цель: установить взаимосвязь искусства оригами и науки математики.
Задачи:
изучить литературу и другие источники информации по данному вопросу;
изучить историю оригами, основные этапы развития оригами;
рассмотреть базовые формы и приемы оригами;
исследовать связь математики и оригами;
провести мастер-класс своим одноклассникам по изготовлению моделей
Методы исследования(практические):
Изучение литературы.

Построение оригами.
Эксперимент, опрос
Анализ проведённой работы.
Оригами увлекательное занятие. Оригинальная идея для подарка и украшения. Интересный способ изучения предмета математика.
Над нашей исследовательской работой, мы работали почти 3 месяца. Посещали школьную библиотеку, искали информацию в Республиканской детско-юношеской библиотеке имени В.Х. Колумба, а так же в Национальной библиотеке имени С.Г. Чавайна, использовали ресурсы Интернет-сайтов, книги из домашней библиотеки.
1.1. Из истории орига
ми В древности Китае бумагу использовали самым различным образом, в том числе и в религиозных обрядах. Например, изначально было принято на похоронах вместе с покойником сжигать и весь его домашний скарб — чтобы обеспечить ему дальнейший путь на небесах. Однако позже из бережливости реальные вещи умершего были заменены специальными полосками бумаги, на которых писались лишь их названия (подобные полоски бумаги с напечатанными пожеланиями процветания и счастья в наши дни можно купить в мелочных лавках Китая). Из бумаги же изготовлялись и разнообразные полезные в быту вещи, вроде знаменитых подвесных фонариков. При их изготовлении использовался и прием складывания. Однако складывание фигурок из квадратных листов бумаги не получило в Китае такого же мощного развития, как в Японии. Вероятно, это объясняется тем, что японцы использовали бумагу не только для письма, производства ширм, зонтиков, окон и даже одежды, но и для наглядной демонстрации некоторых мировоззренческих идей философии дзен-буддизма.
Из бумаги же изготовлялись и разнообразные полезные в быту вещи, вроде знаменитых подвесных фонариков. При их изготовлении использовался и прием складывания. Однако складывание фигурок из квадратных листов бумаги не получило в Китае такого же мощного развития, как в Японии. Вероятно, это объясняется тем, что японцы использовали бумагу не только для письма, производства ширм, зонтиков, окон и даже одежды, но и для наглядной демонстрации некоторых мировоззренческих идей философии дзен-буддизма.
Вообще же красоту, скрытую в вещах, японцы открыли в IX-XII веках, в эпоху Хэйан (794-1185 гг) и даже обозначили особым понятием «моно-но-аварэ». Это открытие идет от синто, веры в то, что каждая вещь, каждое явление, даже слова, содержат в себе ками – божество. Синтоизм, вообще, очень похож на наше язычество. Для синтоистов ками живет, поселяется особенно охотно во всем, что необычно. Например, в бумаге. А тем более в закрученном в мудреный зигзаг гохэй, который висит и сегодня перед входом в синтоистские святилища и указывает на присутствие божества в храме. Существует 20 вариантов складывания гохэй, и те, которые сложены особенно необычно, привлекают ками. С IX века в Японии живет обычай укреплять гохэй на поясах борцов сумо перед началом схватки.
Существует 20 вариантов складывания гохэй, и те, которые сложены особенно необычно, привлекают ками. С IX века в Японии живет обычай укреплять гохэй на поясах борцов сумо перед началом схватки.
До сих пор складывают в Японии ката-сиро – восемь кукол из белой бумаги, которых расставляют для предотвращения несчастий по всем восьми направлениям пространства; складывают гофу — бумажные амулеты; и нагаси-бина – символ семейной гармонии: он и она в бумажном кимоно на круглом ложе. Для изгнания злых духов и очищения храмов синтоисты до сих пор пользуются харам-гуси – метелкой, сложенной из полосок белой бумаги. Вообще роль бумаги в синто очень велика, и изделиям из нее придается эзотерический смысл.
В периоды Камакура (1185 — 1333 гг.) и Муромати (1333 — 1573 гг.)оригами выходит за пределы храмов и достигает императорского двора. Аристократия и придворные должны были обладать определенными навыками и в искусстве складывания. Записки, сложенные в форме бабочки, журавля, цветка или абстрактной геометрической фигуры были символом дружбы или доброго пожелания для любимого человека. Ими удавалось порой выразить больше внимания, любви, чем это можно было сделать словами. Умение складывать стало одним из признаков хорошего образования и изысканных манер. Различные знатные семьи использовали фигурки оригами как герб и печать. Придворная дама Мурасаки Сикибу, жившая в XI в, упоминает в своей книге «Гандзи моно гатари» («Повесть о блистательном принце Гандзи») о разновидности оригами-искусстве складывания писем, когда само письмо превращалось в замысловатый конверт с украшением.
Ими удавалось порой выразить больше внимания, любви, чем это можно было сделать словами. Умение складывать стало одним из признаков хорошего образования и изысканных манер. Различные знатные семьи использовали фигурки оригами как герб и печать. Придворная дама Мурасаки Сикибу, жившая в XI в, упоминает в своей книге «Гандзи моно гатари» («Повесть о блистательном принце Гандзи») о разновидности оригами-искусстве складывания писем, когда само письмо превращалось в замысловатый конверт с украшением.
В периоды Адзути-Момояна (1573 — 1603 гг.) и Эдо (1603 — 1867 гг.) оригами из церемониального искусства превратилось в популярное времяпрепровождение. Тогда бумага перестала быть предметом роскоши и оригами начало распространяться и среди простого народа. Именно тогда, триста-четыреста лет тому назад, изобретается ряд новых фигурок, которые позже становятся классическими. Среди них и японский журавлик (цуру) — традиционный японский символ счастья и долголетия. Искусство оригами в Японии стало традицией, которая передается из поколения в поколение в основном по женской линии. Историки оригами утверждают, что по манере складывания и набору фигурок можно было определить провинцию Японии, в которой выросла и обучалась девушка.
Историки оригами утверждают, что по манере складывания и набору фигурок можно было определить провинцию Японии, в которой выросла и обучалась девушка.
Итак, к появлению оригами причастен синтоизм, обративший внимание буддистов на тайну листа бумаги. Немаловажным оказалось также и сходство звучания японских слов «бумага» и «божество» — «ками». В представлениях японцев возникла некая мистическая связь между религиозными ритуалами и изделиями из сложенной бумаги. Не случайно первые оригами появляются в синтоистских храмах. Один из ритуалов с их использованием состоял в изготовлении небольших бумажных коробочек санбо, которые наполняли кусочками рыбы и овощей, поднося их в качестве жертвоприношений богам.
1.2. Первые книги по оригами. Первым японским изданием по оригами считается книга «Семба-цуру ориката», которая вышла в свет в 1797 г. Перевод ее названия «как сложить тысячу журавлей» явно намекает на старинную легенду, утверждающую, что тысяча сложенных классических бумажных птиц помогает осуществить желания. Книга целиком посвящена складыванию одной-единственной модели — журавлика. Разнообразие же 49 вошедших в нее моделей строится на различном сочетании журавликов между собой. Например, они могут иметь вид гирлянды, в которой фигурки соединены кончиками крыльев или клювами. Для складывания такой конструкции делают заготовки из полос или прямоугольников с недоведенными до конца надрезами, которые превращают заготовки в наборы квадратиков. Автором «Сембадзуру ориката» считается настоятель храма Рокан. В том же 1797 г. он выпустил книгу «Чашингура ориката», в которой было показано, как с помощью складывания и ножниц сделать из бумаги главных персонажей популярной в то время пьесы «Чашингура».
Книга целиком посвящена складыванию одной-единственной модели — журавлика. Разнообразие же 49 вошедших в нее моделей строится на различном сочетании журавликов между собой. Например, они могут иметь вид гирлянды, в которой фигурки соединены кончиками крыльев или клювами. Для складывания такой конструкции делают заготовки из полос или прямоугольников с недоведенными до конца надрезами, которые превращают заготовки в наборы квадратиков. Автором «Сембадзуру ориката» считается настоятель храма Рокан. В том же 1797 г. он выпустил книгу «Чашингура ориката», в которой было показано, как с помощью складывания и ножниц сделать из бумаги главных персонажей популярной в то время пьесы «Чашингура».
В 1845 г. в Японии издается книга «Кан-но-мадо», что в литературном переводе означает «зимнее окно», или точнее «окно середины зимы». Она включает инструкции, большей частью словесные, как складывать несколько десятков классических фигурок из бумаги и графические иллюстрации готовых моделей. Знатоки истории оригами утверждают, что именно в «Кан-но-мадо» впервые печатается схема складывания базовой формы «лягушка» и самой фигурки на этой основе. Появление этой книги в период Токугава (1603 – 1867 гг) не случайно. Именно это время характеризуется началом «демократизации» оригами — превращения этого занятия из ритуально-храмового действа в популярный досуг. Название книги указывает на оригами как на занятие, с помощью которого можно приятно скоротать длинный зимний вечер. Но есть и иное толкование названия – как намек на свет скромных знаний, которые можно из нее почерпнуть.
Знатоки истории оригами утверждают, что именно в «Кан-но-мадо» впервые печатается схема складывания базовой формы «лягушка» и самой фигурки на этой основе. Появление этой книги в период Токугава (1603 – 1867 гг) не случайно. Именно это время характеризуется началом «демократизации» оригами — превращения этого занятия из ритуально-храмового действа в популярный досуг. Название книги указывает на оригами как на занятие, с помощью которого можно приятно скоротать длинный зимний вечер. Но есть и иное толкование названия – как намек на свет скромных знаний, которые можно из нее почерпнуть.
В 1879 г директор школы для девочек Саки Нобузоу сделал для своих маленьких учениц книгу по оригами, содержащую инструкцию складывания 20 несложных классических фигурок. В 1885 г Окамото Консеки издал книгу для детей по оригами «Ориката», которая позже была переведена на английский язык.
1.3. Распространение оригами по миру. Новый этап в развитии оригами начался после второй мировой войны и связан с именем знаменитого японского мастера Акиро Йошизава. Он родился в 1911 г и сыграл в истории оригами уникальную роль. С помощью изобретенных им несложных условных знаков (см. приложение 1) процесс складывания любого изделия оказалось возможным представить в виде серии рисунков-чертежей. Акиро Йошизава изобрел сотни новых, ранее не известных, фигурок. Он не только доказал, что искусство складывания может быть авторским, но и способствовал его широчайшему распространению. В течение нескольких лет Японское министерство иностранных дел посылало его в многочисленные поездки по странам Европы, потому что развитое и поддержанное им традиционное японское искусство стало международным средством мира и дружбы без слов.
Он родился в 1911 г и сыграл в истории оригами уникальную роль. С помощью изобретенных им несложных условных знаков (см. приложение 1) процесс складывания любого изделия оказалось возможным представить в виде серии рисунков-чертежей. Акиро Йошизава изобрел сотни новых, ранее не известных, фигурок. Он не только доказал, что искусство складывания может быть авторским, но и способствовал его широчайшему распространению. В течение нескольких лет Японское министерство иностранных дел посылало его в многочисленные поездки по странам Европы, потому что развитое и поддержанное им традиционное японское искусство стало международным средством мира и дружбы без слов.
В начале XX века Япония широко открыла двери остальному миру, и европейцы начали знакомиться с классическими фигурками, выполненными в технике оригами: лягушкой, рыбой, журавликом, цветком ириса.
Однако было бы совершенно несправедливо утверждать, что Европа до этого времени была совершенно незнакома со складыванием. Испания может похвастаться своим собственным, независимым, открытием некоторых фигурок, например птички — «пахариты». Так называется древняя классическая фигурка, ставшая символом оригами в Испании. Известный оригамист Винсенте Паласиос считает, что многое указывает на появление этой модели впервые в Толедо в XII в. Если это предположение, верно, то, без сомнения, пахарита является первой традиционной сложенной европейской фигуркой (возможно, одной из первых во всем мире).
Испания может похвастаться своим собственным, независимым, открытием некоторых фигурок, например птички — «пахариты». Так называется древняя классическая фигурка, ставшая символом оригами в Испании. Известный оригамист Винсенте Паласиос считает, что многое указывает на появление этой модели впервые в Толедо в XII в. Если это предположение, верно, то, без сомнения, пахарита является первой традиционной сложенной европейской фигуркой (возможно, одной из первых во всем мире).
Первые упоминающиеся в старинных европейских документах мельницы, изготавливающие бумагу, существовали в Толедо уже в XII веке (в Италии они появились на столетие позже). Само слово «пахарита» (букв. — птица) применительно к фигуркам имеет в Испании два значения — название конкретной модели, или вообще любая фигурка, сложенная из бумаги. Само искусство складывания фигурок из бумаги называется в Испании «делать пахариты», а сами фигурки – «различные другие пахариты». Сохранился датированный 1563 годом рисунок Антона Ван Дер Вингерде «Астрологический квадрат, превращающийся в пахариту, на фоне г. Толедо».
Толедо».
И все же бумага была материалом редким и дорогим. Чаще (в Европе) складывали ткань — воротники (в костюмах XVI-XVII вв.), чепцы и другие головные уборы, которые носили сестры милосердия, монахини, горничные.
В начала XIX века немецкий педагог, создатель первых детских садов Фридрих Фребель впервые начал пропагандировать складывание из бумаги как дидактический метод для объяснения детям некоторых простых правил геометрии. Возможно, именно с его подачи школьники разных стран мира теперь знакомы с небольшим набором «фольклорных» фигурок из бумаги.
Любителем оригами был Льюис Керрол — автор «Алисы в Стране Чудес» и «Алисы в Зазеркалье», преподававший математику в Оксфорде. Записи в дневнике Кэррола свидетельствуют о том, какой восторг охватил его, когда он научился складывать из бумаги игрушку, издававшую при сильном взмахе ею громкий хлопок.
Умел складывать фигурки из бумаги и русский писатель Лев Толстой. В черновике к статье «Что такое искусство» он пишет: «Нынешней зимой одна мама научила меня делать из бумаги, складывая и выворачивая ее известным образом, петушков, которые, когда их дергаешь за хвост, махают крыльями. Выдумка эта от Японии. Я много раз делал этих петушков детям, и не только дети, но всегда все присутствующие большие, не знавшие этих петушков, и господа, и прислуга развеселялись и сближались от этих петушков, все удивлялись и радовались: как похоже на птиц эти петушки махают крыльями. Тот, кто выдумал этого петушка, от души радовался, что ему так удалось сделать подобие птицы, и чувство это передается, и потому, как ни странно сказать, произведение такого петушка есть настоящее искусство».
Выдумка эта от Японии. Я много раз делал этих петушков детям, и не только дети, но всегда все присутствующие большие, не знавшие этих петушков, и господа, и прислуга развеселялись и сближались от этих петушков, все удивлялись и радовались: как похоже на птиц эти петушки махают крыльями. Тот, кто выдумал этого петушка, от души радовался, что ему так удалось сделать подобие птицы, и чувство это передается, и потому, как ни странно сказать, произведение такого петушка есть настоящее искусство».
Выдающийся испанский поэт и философ Мигель де Унамуно написал пародийно-серьезный трактат по оригами, и придумал новый особый способ складывания бумаги, позволивший ему создать много новых забавных фигурок. Описание тех фигурок, которые он складывал за чашкой кофе, можно найти в английском переводе его «Очерков и монологов» (M. Unamuno, Essays and Soliloquies, Knopf, 1925). Ортега-и-Гарсет в книге о своем друге Унамуно рассказывает, как однажды философ сложил из бумаги несколько фигурок для маленького мальчика, который спросил его, разговаривают ли между собой птички.
В 1937 г. В Лондоне выходит в свет книга Маргарет Кемпбелл «Изготовление бумажных игрушек», в которой впервые упоминаются три традиционные на востоке базовые формы – «водяная бомбочка», «птица», «лягушка». В 1946 г. схема складывания класического японского журавлика публикуется в одном из английских детских журналов.
В международной литературе по оригами давно сложился определенный набор условных знаков, необходимых для того, чтобы зарисовать схему складывания даже самого сложного изделия. Условные знаки играют роль своеобразных «нот», следуя которым можно воспроизвести любую работу. Помимо знаков, существует небольшой набор приемов, которые встречаются достаточно часто. Обычно они даются в книгах без комментариев. Считается, что любой новичок умеет выполнять их на практике. Международные условные знаки вместе с набором несложных приемов и составляют своеобразную «азбуку» оригами, с которой должен быть знаком любой складыватель. Большая часть условных знаков была введена в практику еще в середине XX века известным японским мастером Акирой Йошизавой. В последние десятилетия к этим знакам добавилось несколько новых. К введению любых дополнительных обозначений следует относиться очень осторожно, и уж, конечно, совсем не стоит «изобретать велосипед» и пытаться записывать схемы складывания как-то по-своему. Все обозначения в оригами можно разделить на линии, стрелки и знаки. (См. Приложение1.)
В последние десятилетия к этим знакам добавилось несколько новых. К введению любых дополнительных обозначений следует относиться очень осторожно, и уж, конечно, совсем не стоит «изобретать велосипед» и пытаться записывать схемы складывания как-то по-своему. Все обозначения в оригами можно разделить на линии, стрелки и знаки. (См. Приложение1.)
Многие фигурки оригами на начальном этапе складываются одинаково, то есть имеют одну основу — базовую форму. База – это самая простая уже сложенная форма, из которой со временем могут появиться множество различных фигурок.
Сегодня в мире существует целых 11 базовых форм (Приложение 2).
Простые базовые формы: треугольник, книга, дверь, воздушный змей;
Средние базовые формы: блин, рыба, двойной треугольник, двойной квадрат;
Сложные базовые формы: птица, катамаран, лягушка.

Часто в книгах об оригами даже не приводятся схемы базовых форм оригами, подразумевается, что мастер оригами уже с ними знаком.
2.2. Виды и техника оригамиМодульное оригами
Одной из популярных разновидностей оригами является модульное оригами, в котором целая фигура собирается из многих одинаковых частей (модулей). Каждый модуль складывается по правилам классического оригами из одного листа бумаги, а затем модули соединяются путём вкладывания их друг в друга, появляющаяся при этом сила трения не даёт конструкции распасться. Одним из наиболее часто встречающихся объектов модульного оригами является кусудама, объёмное тело шарообразной формы.
Простое оригами
Простое оригами — стиль оригами, придуманный британским оригамистом Джоном Смитом, и который ограничен использованием только складок горой и долиной. Целью оригами является облегчение занятий неопытным оригамистам, а также людям с ограниченными двигательными навыками. Данное выше ограничение означает невозможность многих (но не всех) сложных приёмов, привычных для обычного оригами, что вынуждает к разработке новых методов, дающих сходные эффекты.
Данное выше ограничение означает невозможность многих (но не всех) сложных приёмов, привычных для обычного оригами, что вынуждает к разработке новых методов, дающих сходные эффекты.
Складывание по развёртке
Развёртка (англ. creasepattern; паттерн складок) — один из видов диаграмм оригами, представляющий собой чертёж, на котором изображены все складки готовой модели. Складывание по развёртке сложнее складывания по традиционной схеме, однако, данный метод даёт не просто информацию, как сложить модель, но и как она была придумана — дело в том, что развёртки используются при разработке новых моделей оригами. Последнее также делает очевидным факт отсутствия для некоторых моделей иных диаграмм, кроме развёртки.
Мокрое складывание
Мокрое складывание — техника складывания, разработанная Акирой Йошизавой и использующая смоченную водой бумагу для придания фигуркам плавности линий, выразительности, а также жесткости. Особенно актуален данный метод для таких негеометрических объектов, как фигурки животных и цветов — в этом случае они выглядят намного естественней и ближе к оригиналу. Не всякая бумага подходит для мокрого складывания, а лишь та, в которую при производстве добавляют водорастворимый клей для скрепления волокон. Как правило, данным свойством обладают плотные сорта бумаги.
Особенно актуален данный метод для таких негеометрических объектов, как фигурки животных и цветов — в этом случае они выглядят намного естественней и ближе к оригиналу. Не всякая бумага подходит для мокрого складывания, а лишь та, в которую при производстве добавляют водорастворимый клей для скрепления волокон. Как правило, данным свойством обладают плотные сорта бумаги.
Базовые складки или схемы в оригами
Базовые складки в оригами, или формы, как еще их можно называть, это простейшие фигуры, на основе которых потом складывается большинство моделей оригами. Часто в книгах об оригами даже не приводится их схем базовых форм оригами, подразумевается что мастер оригами уже с ними знаком
Искусство складывания из бумаги, или оригами, насчитывает уже несколько сотен лет. В последние десятилетия в данном виде искусства стали использоваться достижения математики. Так как математика это есть умение решать задачи, причем не только стандартные, но еще и требующие независимости мышления, здравого смысла, оригинальности, изобретательности.
По мнению дизайнера оригами Адзума Хидэаки, если развернуть фигурку оригами и посмотреть на складки – то можно увидеть лишь обилие многоугольников, соединенных друг с другом. В сложенном же виде оригами представляет собой многогранник, фигуру с множеством плоских поверхностей, а когда фигура разложена и показаны все складки, то мы можем увидеть множество геометрических фигур.
С точки зрения математики оригами, это точное определение местоположения одной или более точек листа, задающих складки, необходимые для формирования окончательного объекта. Процесс складывания подразумевает выполнение последовательности точно определенных действий по следующим правилам, которые перекликаются с законами математики:
точность выполнения инструкции;
точки определяются пересечениями линий;
линия определяется либо краем листа, либо линией сгиба бумаги.
все линии прямые и делятся на два вида параллельные и перпендикулярные.

В наше время оригами с математической точностью шагает по планете семимильными шагами. Ученные придумали использовать приёмы оригами в космосе, а именно Миура-ори — схема жесткого складывания, которая использовалась для развертывания больших установок солнечных батарей на космических спутниках.
Математика это одна из сторон оригами и наоборот оригами является одной из направляющих математики.
Как связано искусство оригами и точная наука математика? Этот вопрос мы решили изучить.
Мы проанализировали базовые формы оригами и заметили, что уже при первом знакомстве с этим искусством мы узнаем о таких простых формах, как прямоугольник и треугольник. Когда складываем простую форму, то знакомимся с квадратом, согнув углы которого к центру можно увидеть, что квадрат может состоять из четырёх одинаковых треугольников. Складывая форму «Воздушный змей», знакомимся с ромбом. Азбука оригами включает в себя такие геометрические понятия, как точка и линия.
Таким образом, оригами и математика (а именно геометрия) неразрывно связаны. При изготовлении различных моделей оригами мы используем множество понятий из математики (такие как точка, линия, квадрат, прямоугольник, треугольник и т.д.).
3.1. Ориганометрия.
Из Опроса, который мы провели среди параллели 5 классов, убедились в том, что об ориганометрии большинство не слышали, нежели чем, об оригами. (Приложение 3).
И правда, когда мы начали искать информацию о ориганометрии, мы столкнулись с минимализмом информации. И так, что мы нашла.
Оригами тесно связано с геометрией, даже есть такое понятие «оригамометрия». Поскольку оригами имеет дело с трансформацией одномерных фигур в трёхмерные, зная кое-какие секреты, можно без традиционных математических принадлежностей измерять углы, создавать идеально равносторонние фигуры и т.п.
Ориганометрия — это сочетание оригами и геометрии, которое несет в себе оригинальность другого подхода к геометрическим задачам.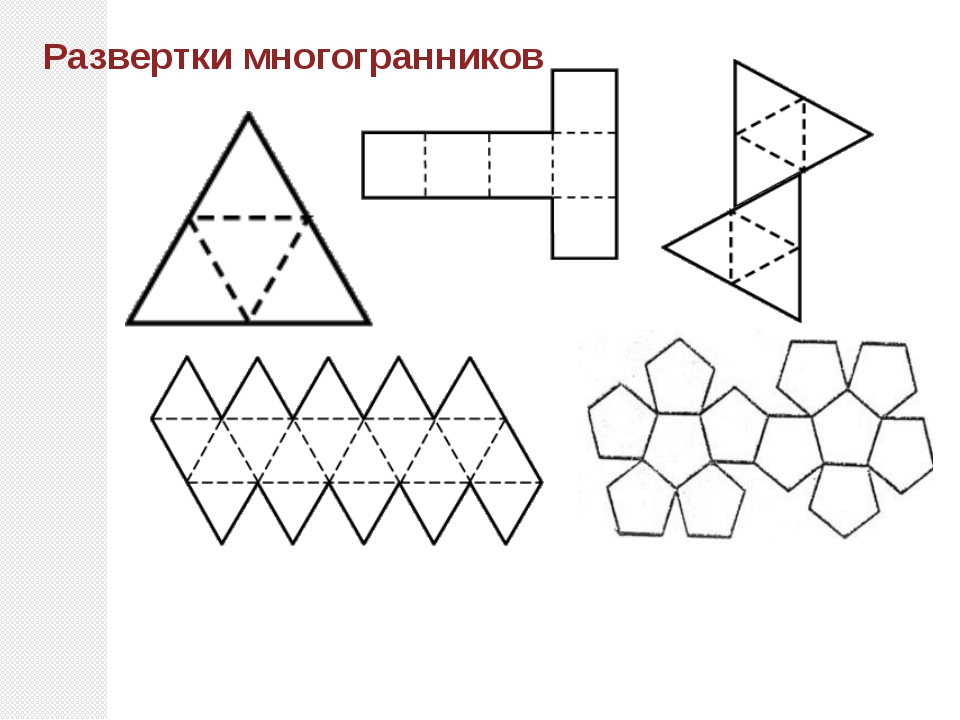 Ориганометрия – новая область геометрии, возникла в конце 20 века. Исходя из основополагающих принципов, из любого листа бумаги (не обязательно прямоугольного!) с помощью его перегибания можно получить квадрат. Это означает, что, решая конкретную задачу, всегда можно начинать с квадрата. По словам японского математика Хумиаки Хузита, живущего в Италии, ориганометрия базируется на следующих шести аксиомах, на основе которых допустимы действия с бумагой:
Ориганометрия – новая область геометрии, возникла в конце 20 века. Исходя из основополагающих принципов, из любого листа бумаги (не обязательно прямоугольного!) с помощью его перегибания можно получить квадрат. Это означает, что, решая конкретную задачу, всегда можно начинать с квадрата. По словам японского математика Хумиаки Хузита, живущего в Италии, ориганометрия базируется на следующих шести аксиомах, на основе которых допустимы действия с бумагой:
1.Существует единственный сгиб, проходящий через две данные точки.
2.Существует единственный сгиб, совмещающий две данные точки.
3.Существует сгиб, совмещающий две данные прямые.
4.Существует единственный сгиб, проходящий через данную точку и перпендикулярный данной прямой.
5.Существует сгиб, проходящий через данную точку и помещающий другую данную точку на данную прямую.
6.Существует сгиб, помещающий каждую из двух данных точек на одну из двух данных пересекающихся прямых.
3.2. Задачи
Правильные многоугольники и способы их изготовления из квадрата с помощью ориганометрии:
Треугольник
Пятиугольник
Шестиугольник
Восьмиугольник
В рамках поисковой работы мы сначала рассмотрели некоторые базовые модели оригами и выяснили их связь с математическими понятиями. Мы решили взять несколько стандартных схем оригами, и выяснить какие геометрические фигуры используются в них. Для этого необходимо снова рассмотреть основы оригами. (См. Приложение 1,2).
И сейчас мы можем сделать вывод, что при работе с оригами следует знать следующие фигуры: прямая, квадрат, треугольник, угол, ромб, диагональ, биссектриса.
4.1. Эксперимент.
Проведем эксперимент по сложению оригами. И сразу выпишем, знания, каких геометрических фигур нам были нужны.
И сразу выпишем, знания, каких геометрических фигур нам были нужны.
Схема 1. «Кошка»
Вывод:
Встречаются понятия таких геометрических фигур как: квадрат, треугольник, прямая..
Схема 2: «Журавль»
Вывод:
Встречаются понятия таких геометрических фигур как: треугольник, квадрат, середина, линия, угол
Как наглядное средство лист бумаги применяется в обучении математике с давних пор. Но на уроках математики важно не то, какую фигурку вы сложили из бумаги, а наоборот. Разверните любую бумажную поделку. Линии сгиба образовали треугольники, квадраты, четырехугольники. К тому же, разворачивая поделку, можно наблюдать преобразование пространственной фигуры в плоский лист бумаги. А значит, упражнения с листом бумаги позволяют знакомиться с различными геометрическими фигурами и изучать их простейшие свойства.
Исходя из всего вышеизложенного нами, мы можем сделать выводы:
искусство оригами тесно связано с математикой и помогает ее изучать;
данная тема представляет большие возможности для проявления исследовательских и творческих умений при решении задач.
Гипотеза: Искусство оригами тесно связано с математикой и может стать хорошей основой для ее изучения подтвердилась.
Главный фактор возрастания популярности этого искусства — это энтузиазм его приверженцев. Оригами входит в факультативную программу обучения многих ведущих образовательных центров для детей. Оригами – и детская забава, и элемент дизайна, и неотъемлемый атрибут народных праздников во многих странах мира. Существуют театры, где персонажами и декорациями являются бумажные фигурки.
Занятие оригами оказывает положительное влияние на развитие детей. Специалисты-медики считают, что оно позволяет полнее использовать ресурсы психики, гармонично развивая оба полушария головного мозга.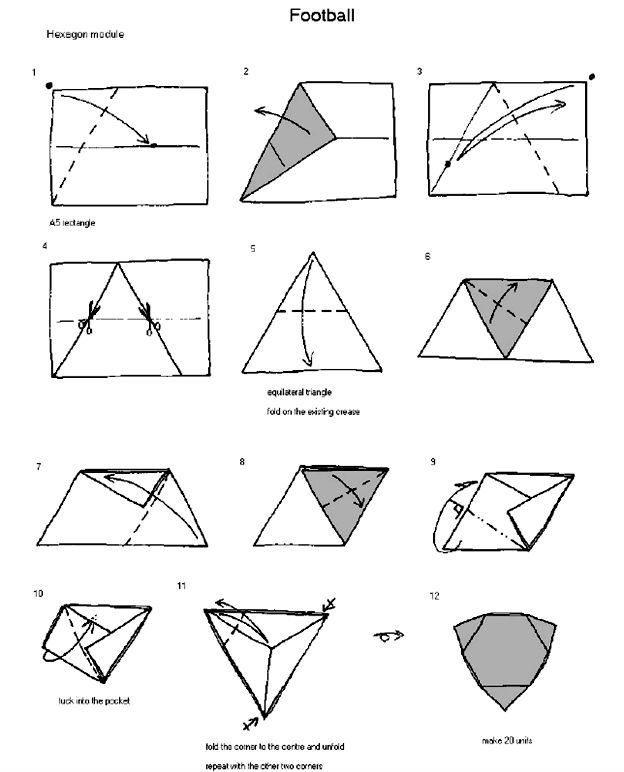 У ребят совершенствуются мелкая моторика рук, движения пальцев становятся более точными (что немаловажно для школьников начальных классов, овладевающих письмом), вырабатывается усидчивость. Ведь чтобы получилась красивая фигурка, нужны аккуратность, внимание, сосредоточенность. Кроме того, оригами развивает память, мышление, пространственное воображение, сообразительность. Неспроста это занятие применяют в своей практике врачи-логопеды. Помогает оно и людям с нарушениями опорно-двигательного аппарата, с психическими расстройствами.
У ребят совершенствуются мелкая моторика рук, движения пальцев становятся более точными (что немаловажно для школьников начальных классов, овладевающих письмом), вырабатывается усидчивость. Ведь чтобы получилась красивая фигурка, нужны аккуратность, внимание, сосредоточенность. Кроме того, оригами развивает память, мышление, пространственное воображение, сообразительность. Неспроста это занятие применяют в своей практике врачи-логопеды. Помогает оно и людям с нарушениями опорно-двигательного аппарата, с психическими расстройствами.
Нам было очень интересно работать над данной темой. В дальнейшем мы продолжим нашу работу, так как это нам поможет находить новые способы решения некоторых задач, а также при изучении геометрии в 7 классе.
Некоторые ребята из нашего класса заинтересовались оригами, и мы провели для них мастер – класс. Мы создали подарок нашим мальчикам и папам к 23 февраля. (См. Приложение 5)
Белим С.
 Н. Задачи по геометрии, решаемые методами складывания (оригами). [Текст]: приложение к журналу «Оригами»./ С. Н. Белим. – Москва: Издательство Аким, 1998
Н. Задачи по геометрии, решаемые методами складывания (оригами). [Текст]: приложение к журналу «Оригами»./ С. Н. Белим. – Москва: Издательство Аким, 1998Выгонов В.В. Трехмерное оригами: практическое пособие/ В.В. Выгонов. – Москва.: Издательский Дом МСП, 2007
Ильина Н.К.. Оригами. Необычное моделирование для развития фантазии.: практическое пособие/ Н.К.Ильина. — Москва.:РИПОЛ классик,2012
Сержантова Т.Б. Оригами. Лучшие модели./Т.Б.Сержантова. — Москва.: Издательство Айрис-пресс,2010
Черенкова Е.Ф. Простейшие модели оригами: практическое пособие/ Е.Ф.Черенкова. – Москва.: Издательство ДОМ XXI век, 2006
Интернет-ресурсы:
http://www.origami–do.ru
http://www.origami.ru
http://yourorigami.info/2008/01/26/istoriya-proisxozhdeniya-origami.
 html
html
Повторить действие один раз (сзади или на соседней стороне).
Нажать , надавить, вогнуть.
Держать здесь.
Точка, отмечающая угол, край, линию или пересечение линий.
Прямой угол
Равные углы
Следующая картинка-вид отсюда.
Увеличенное изображение.
// //
Равные части или строны.
Линия сгиба «долиной», «на себя»
Стрелка сгиба «долиной», «на себя»
Совместить отмеченные точки
Согнуть и разогнуть
Базовая форма «Блин»
Базовая форма «Треугольник»
Базовая форма «Птица №1″
Схема 1 | Схема 2
Схема 1 | Схема 2
Схема 1 | Схема 2
Базовая форма «Птица №2»
Базовая форма «Катамаран»
Базовая форма «Ромб»
Схема 1 | Схема 2
Схема 1 | Схема 2
Схема 1 | Схема 2
Базовая форма «Дверь»
Базовая форма «Лягушка №1″
Базовая форма «Лягушка №2″
Схема 1 | Схема 2
Схема 1 | Схема 2
Схема 1 | Схема 2
Базовая форма «Рыба №1″
Базовая форма «Рыба №2″
Базовая форма «Бумажный змей»
Схема 1 | Схема 2
Схема 1 | Схема 2
Схема 1 | Схема 2
Базовая форма «Узор»
Базовая форма «Вертушка»
Базовая форма «Квадрат»
Схема 1 | Схема 2
Схема 1 | Схема 2
Схема 1 | Схема 2
Базовая форма «Стол»
Схема 1 | Схема 2
делаем поделку в технике оригами
В наши дни, наверное, из бумаги уже делают все.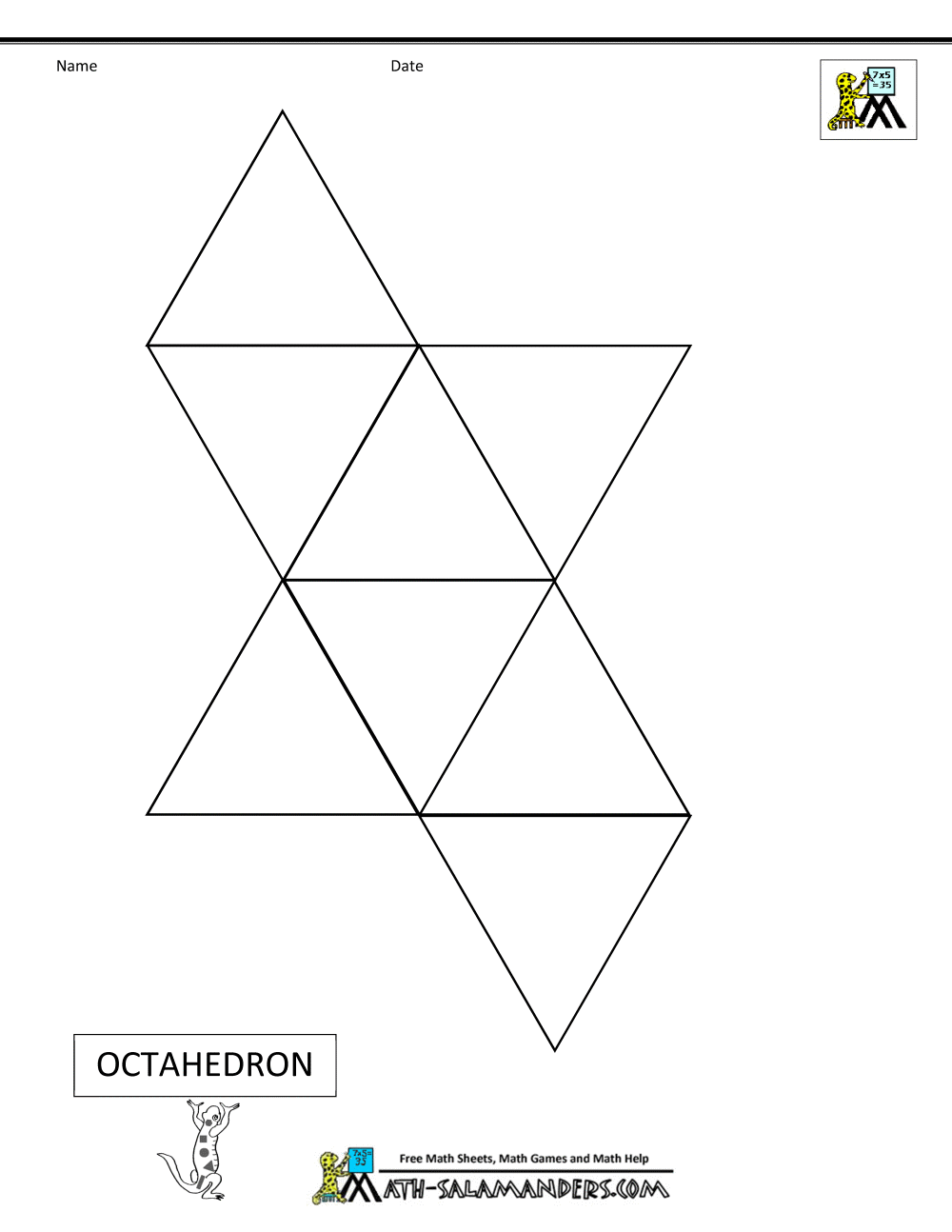 Огромная востребованность, данного продукта обусловлена широкой известностью и обширной сферой применения. Сегодня мы поговорим про объемные фигуры из бумаги своими руками. Для некоторых людей такое хобби перерастает в прибыльную профессию, ведь про их экспонаты можно только сказать, что это настоящее произведение искусства.
Огромная востребованность, данного продукта обусловлена широкой известностью и обширной сферой применения. Сегодня мы поговорим про объемные фигуры из бумаги своими руками. Для некоторых людей такое хобби перерастает в прибыльную профессию, ведь про их экспонаты можно только сказать, что это настоящее произведение искусства.
В технике модульного оригами объемные фигуры из бумаги собираются из большого количества одинаковых частей (модулей). Каждый модуль складывается по правилам классического оригами из одного листа бумаги, а затем модули соединяются путём вкладывания их друг в друга. При этом сила трения не даёт конструкции распасться. В технике модульного оригами часто делают коробочки, плоские и объемные звезды, объекты шарообразной формы, которые в России получили не совсем точное название кусудама, так как первоначально кусудама предполагала сшивание модулей в шар.
Мокрое оригами — ближе к реальности
Есть еще один вид популярного оригами — это мокрое складывание. Для придания плавных линий бумага слегка смачивается с помощью губки или пульверизатора. Чаще всего используется для создания фигурок животных. Мокрая бумага более податлива и после высыхания лучше держит форму. Особенностью является то, что намочив конструкцию снова — можно придать ей другую форму, не порвав бумагу.
Для придания плавных линий бумага слегка смачивается с помощью губки или пульверизатора. Чаще всего используется для создания фигурок животных. Мокрая бумага более податлива и после высыхания лучше держит форму. Особенностью является то, что намочив конструкцию снова — можно придать ей другую форму, не порвав бумагу.
Киригами — объемы из плоскости
В технике киригами можно использовать ножницы и клей. Поделки в технике киригами чем-то напоминают детские книжки-панорамы. Также эту технику часто сравнивают с ‘pop-up’ — открытками. В отличие от традиционных pop-up-открыток, эти бумажные модели обычно надрезают и складывают из одного листа бумаги. Чаще всего разрабатывают трехмерные воспроизведения архитектуры, геометрические узоры и различные повседневные объекты и др.
Кусудама — округлые формы
Техника кусудама имеет тот же принцип, что и модульное оригами. Главным отличием является то, что фигурки имеют шарообразную форму, а детали для соединения могут быть не только вложены одну в другую, но также склеены или сшиты.
Cubecraft — квадратный колобок с многими лицами
Эта современная техника выполнения поделок из бумаги. В этой технике все фигурки складываются по одной схеме. Смысл в том, что можно делать фигурки различных известных персонажей из кино, комиксов, мультфильмов, а также реальных личностей: политических деятелей, музыкантов, актеров и пр. Такие фигурки ставятся на стол в качестве напоминания или просто порадовать взгляд.
Папье-маше — вспоминаем детство
Название техники папье-маше переводится с французского, как «жеваная бумага». Но вы удивитесь, когда узнаете, что родиной этой техники является Китай. Техника заключается в многослойном наклеивании вымоченных в клейстере кусочков бумаги. Затем фигуры из бумаги грунтуются и раскрашиваются. Из папье-маше можно сделать все, что угодно (вазочки, игрушки, кружки), но чаще всего делают маски.
Декупаж — украсить старые вещи
Декупаж в переводе означает «вырезание». Чаще всего техника декупаж используется для старой мебели — вырезаются какие-нибудь драконы или птицы, растения или животные.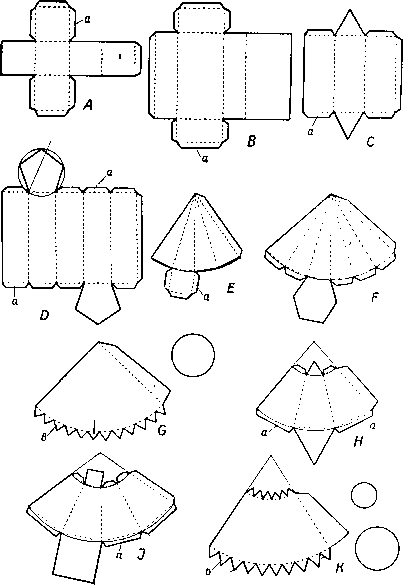 Это придает новый блеск старым вещам. Используется также при создании эксклюзивных предметов интерьера, при оформлении одежды и изготовлении модных аксессуаров.
Это придает новый блеск старым вещам. Используется также при создании эксклюзивных предметов интерьера, при оформлении одежды и изготовлении модных аксессуаров.
Торцевание — квиллинг по-новому
В технике торцевания получается изготовить красивые открытки или даже картины. В квиллинге используются длинные полоски, которые накручиваются на тонкую палочку. Здесь же нарезаются небольшие квадраты. Затем, к центру квадрата прикладывается палочка, и на нее накручивается этот квадратик. Получившаяся деталь наклеивается на основу. Получается иногда необычно и весьма объемно.
Пейп-арт — имитация металла
Эта техника придумана в 2006 году и в своей основе содержит имитацию металла и дерева из бумажных салфеток. Техника имитирует резьбу по дереву или чеканку из металла. Окраска и патинирование придает натуральность текстурам. Смоченные в воде полоски из салфеток скручиваются в нитки, затем из них выкладывается узор и закрепляют клеем. После высыхания остается только покрасить и придать естественность.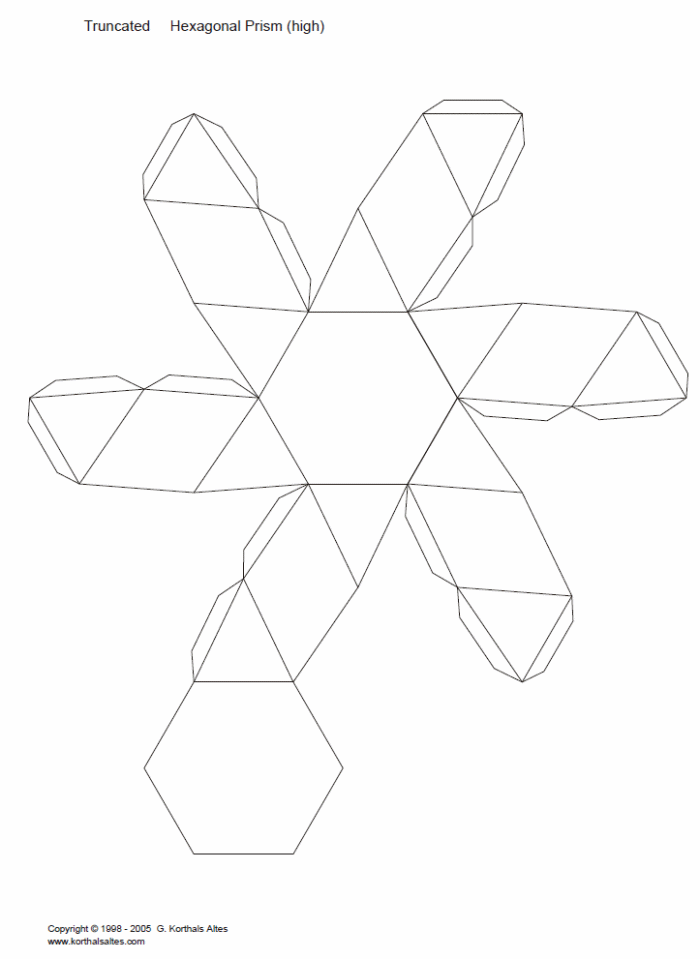
Айрис фолдинг — «радужное складывание»
Чтобы сделать поделку в этой технике, нужно нарезать несколько полосок бумаги разного цвета и уложить их по спирали или другим причудливым способом. Выглядит все это как многогранная фигура. Наложение полупрозрачных бумаг друг на друга дает интересные эффекты при декорировании.
Пергамано — кропотливый труд
Узоры и украшения в этой технике выполняются или пергаментной бумаге с помощью перфорирования и тиснения. Чаще всего техника пергамано используется в изготовлении открыток и приглашений.
Катагами — нужен острый нож
Еще немного Японского бумажного искусства. Катагами — искусство вырезания целых картин из рисовой бумаги с помощью специального острого ножа и трафарета или по нарисованной линии. Чаще всего используется для картин.
Коллаж — это изображение, составленное из различных бумажных кусочков (обоев, газет, журналов, фотографий и пр.), отличающихся по цвету и фактуре. Раньше вырезали картинки из журналов, газет, книг и украшали ими вещи (вспомните бабушкин чемодан или трюмо). Сейчас эта старинная техника вновь стала модной и широко распространена в различных странах при декорировании сумочек, шляпок, подносов, ёлочных украшений, солнечных часов, шкатулок, посуды, упаковок и т. д.
Сейчас эта старинная техника вновь стала модной и широко распространена в различных странах при декорировании сумочек, шляпок, подносов, ёлочных украшений, солнечных часов, шкатулок, посуды, упаковок и т. д.
Бумажное моделирование — бумага превращается…
Особого интереса, заслуживает бумажное моделирование . Вы можете создать практически любую объемную фигуру из бумаги своими руками. Начиная от военной техники, памятников архитектуры и заканчивая различными видами животных, как известных всем, так и вымышленных. Конечно, в идеале нужно уметь делать все (чертежи, детали и прочее) своими руками, но для начала можно воспользоваться интернетом. Через поиск Вы сможете отыскать массу чертежей и макетов, которые можно распечатать на принтере, вырезать и склеить. Есть даже специальные сайты, которые хранят чертежи бумажных моделек: самолетов, автомобилей, героев фильмов и мультфильмов.
Все перечисленные техники поделок из бумаги имеют свои нюансы, преимущества и недостатки. Но самое главное, при выборе каким видом бумажного искусства заняться, я советую руководствоваться исключительно собственным сердцем. Для того, чтобы сделать завораживающую фигурку, надо по-настоящему любить это дело.
Но самое главное, при выборе каким видом бумажного искусства заняться, я советую руководствоваться исключительно собственным сердцем. Для того, чтобы сделать завораживающую фигурку, надо по-настоящему любить это дело.
Это кропотливая работа, которая требует внимательности и терпения, и только при сильном желании можно все сделать, так как надо. Наградой для Вас, могут стать восхищенные взоры друзей и похвалы в Ваш адрес.
Бумажные изделия смотрятся очень красиво, если все ровненько вырезать и собрать. Главное, что для создания таких фигур не требуется специальных навыков. Достаточно внимательно все соединить. Немного попрактиковавшись, у Вас станет все получаться значительно быстрее и ровнее.
Пример, насколько необычными могут быть фигуры из бумаги, можно увидеть из нижеприведенного видео. Советую всем посмотреть, ведь это действительно необычно и шедеврально.
Красивые аппликации из фигур помогают развить хорошее мышление у маленьких детей. Они положительно влияют на детское подсознание, тем самым формируя представления о внешнем мире.
Перед тем как приступать к развивающим занятиям, необходимо объяснить, что собой представляют геометрические фигуры. Именно они лежат в основе интересного занятия. Через некоторое время ребенок научится самостоятельно вырезать бумажные элементы.
В нашем материале представлены подробные инструкции и чертежи для развивающих аппликаций. Облегчить поставленную задачу помогают готовые эскизы. По их строению подбирают необходимые элементы для создания необычной картины.
Занятия должны подбираться исходя из возрастной категории вашей крохи. Для маленьких детей лучше всего выбирать аппликации состоящие из 4-5 геометрических фигур. Различие цветовой палитры способствует хорошему запоминанию и тренировке памяти.
Геометрическая аппликация « Транспорт»
Как сделать геометрическую аппликацию? На самом деле все достаточно просто. При выборе задания рекомендуется ознакомиться с предпочтением вашего чада. Например, девочкам больше нравятся цветы, птицы, звери. Мальчики чаще всего выбирают машины, роботов и т.д.
Мальчики чаще всего выбирают машины, роботов и т.д.
Что же касается цветового сочетания, то детям с импульсивным характером лучше всего подбирать светлые или пастельные оттенки. Они формируют максимальную концентрацию внимания и усидчивость. Помимо этого, такие меры положительно сказываются на эмоциональном состоянии.
Предлагаем вашему вниманию аппликацию в виде транспорта. Она состоит из простых геометрических фигур. Это занятие придется по душе для детей в возрасте от 3 до 4,5 лет. Оно формирует трудолюбие, упорство и аккуратность.
Перед тем как приступить к рабочему процессу, необходимо подготовить следующие инструменты и материалы:
- простой карандаш;
- линейка;
- клей ПВА;
- ножницы;
- цветная бумага;
- изображение машины;
- кисточка.
Процесс создания аппликации проходит в несколько простых этапов:
- Начинаем вырезать фигуры из которых состоит наш «геометрический» транспорт: прямоугольник для основной части корпуса автомобиля, круги для колес, квадрат для крыши.
 Перед тем как приступить к вырезанию предметов, необходимо определиться с их цветовой гаммой.
Перед тем как приступить к вырезанию предметов, необходимо определиться с их цветовой гаммой. - Далее на белом листе бумаги рисуем дорогу, по которой будет передвигаться транспорт. После этого по центру приклеиваем прямоугольник. Над ним клеем крышу. Каждый элемент смазываем небольшим количеством клеевого состава. Когда крыша и кузов высохли, можно переходить к колесам.
Аппликация практически готова. Здесь можно дать волю детской фантазии. Пусть ребенок сам нарисует двери и окна своему автомобилю.
Аппликации из геометрических фигур « Животные»
Эта методика развития направлена на возраст от 5 до 6 лет. В это время ребенок уже имеет хорошее представление, из каких фигур состоит тело того или иного животного. Как сделать геометрическую аппликацию для ребенка? Сегодня мы будем клеить собаку.
В составе бумажной конструкции имеется: голова в виде круга, туловище в форме овала, лапы из маленьких прямоугольников и овалов, шея в виде цилиндра. Для украшения в области шеи мы сделаем небольшой бантик из двух треугольников.
Для украшения в области шеи мы сделаем небольшой бантик из двух треугольников.
Перед началом занятий, необходимо подготовить следующие инструменты:
- ножницы;
- линейка;
- кисточка.
Из материалов нам понадобится:
- цветная бумага или картон;
- белый лист бумаги в формате А4;
- клей в виде карандаша.
Мастер класс для геометрических аппликаций своими руками проходит в несколько этапов:
Аккуратно вырезаем геометрические составляющие нашей поделки. Далее каждый элемент фиксируем на своем месте. Опытные педагоги рекомендуют нумеровать каждую деталь. Это позволит ребенку освоить счет и визуальное представление.
Обратную сторону смазываем клеевым составом. Сначала приклеиваем голову, после этого остальные части тела животного. Завершающим действием будет красивый бантик яркого цвета.
На фото геометрических аппликаций изображены чертежи и эскизы. Здесь вы можете подобрать развивающее занятие для вашего ребенка исходя из его возраста и предпочтения.
Здесь вы можете подобрать развивающее занятие для вашего ребенка исходя из его возраста и предпочтения.
Фото геометрических аппликаций
Если вас интересует, как сделать идеальную по формам и граням пирамиду из бумаги существует определенная схема с размерами, чтобы в итоге получилась правильная фигура. Бумажная пирамида может быть оригинальным подарком, сделанным своими руками или просто интересной поделкой.
Благодаря древнему мастерству оригами есть возможность воссоздавать практически любую фигуру из бумаги, в том числе и пирамиду. Существует несколько способов, как создать идеальную фигуру с четкими гранями. Для новичков в этом деле есть легкий пошаговый совет, как сделать фигуру из картона. Данная инструкция будет понятна как взрослым, так и детям.
Пошаговое руководство, как склеить пирамиду из картона:
- На бумажном листе нужно нарисовать один ровный квадрат и три треугольника.
 Каждая сторона квадрата должна быть примерно 15 см. Ширину треугольника стоит сделать такой же, а высоту 27 см.
Каждая сторона квадрата должна быть примерно 15 см. Ширину треугольника стоит сделать такой же, а высоту 27 см. - Ножницами вырезать заготовки не по контуру, а с отступом 3-4 мм, в дальнейшем это будет необходимо при склеивании фигуры.
- Смазать клеем все части, дать ему немного подсохнуть и сложить все детали в единую конструкцию.
- Дать полностью высохнуть поделке и можно приступить к декору.
Как украсить пирамиду — может быть любая воля фантазии. Например, на нее можно наклеить фигурки, обмотать фольгой или раскрасить специальными акриловыми красками.
Материалы и приспособления
Как сделать пирамиду из бумаги схема с размерами – не единственные главные составляющие в изготовлении фигуры.
Для удобства выполнения оригами следует заранее подготовить необходимые материалы и приспособления, чтобы в момент работы все они были под рукой:
- Для изготовления граней могут понадобиться различные материалы. Задействовать можно не только картон, но и пластик, металл, фанеру, стекло или сделать каркас из проволоки.
 Если фигура создана с каким-либо эзотерическим посылом, то бумажную пирамиду советуется изнутри обклеить фольгой. Это нужно для того чтобы в фигуре накапливалась и не рассеивалась положительная энергия. Если внутрь пирамиды поместить несколько небольших магнитов, то изделие будет обладать магнитной энергией.
Если фигура создана с каким-либо эзотерическим посылом, то бумажную пирамиду советуется изнутри обклеить фольгой. Это нужно для того чтобы в фигуре накапливалась и не рассеивалась положительная энергия. Если внутрь пирамиды поместить несколько небольших магнитов, то изделие будет обладать магнитной энергией. - Для поделки стоит обзавестись качественным клеем, который можно купить в канцелярском магазине.
- Пригодятся острые ножницы, чтобы вырезать ровные заготовки для будущей фигуры.
- Также нужны будут линейка, карандаш и ластик на всякий случай .
Для выполнения фигуры не требуется много материалов, все приспособления для пирамиды найдутся почти в каждом доме.
Определяем параметры
Чтобы изделие получилось аккуратным и красивым стоит задать четкие параметры при изготовлении заготовок для будущей пирамиды. Для каждой части может понадобиться отдельный лист бумаги. Можно скачать уже готовые схемы, но их также просто нарисовать самостоятельно.
Главное знать, что ширина треугольника должна быть равна каждой длине грани квадрата.
Высоту геометрической фигуры можно выбрать любую, но рекомендуемая длина, чтобы она была больше на 10-15 см ширины заготовки. Именно при таком соотношении фигура будет смотреться гармонично.
Строим чертеж
Чтобы было проще узнать, как сделать идеальную пирамиду из бумаги или каких-либо других материалов существует схема с размерами. Чертеж – основа для дальнейшего склеивания компонентов для будущей цельной фигуры. Существует несколько видов пирамид, для каждой из них свой чертеж.
Но есть один простой способ, который подходит для детей и новичков в этом деле:
Завершение моделирования
Вырезанную фигуру, нужно склеить по линиям сгибов. Перед тем как соединить части в полную модель на сгибы нужно нанести клей и немного оставить его застыть, чтобы он лучше схватился. После того как изделие будет готово следует его оставить на полчаса, чтобы потом при оформлении оно случайно не расклеилось. В завершающий этап моделирования входит дизайнерское оформление работы.
В завершающий этап моделирования входит дизайнерское оформление работы.
Можно разукрасить пирамиду акриловыми или мерцающими красками, нарисовать на ней фигуры.
Изделие можно обклеить фольгой или бумагой для подарков. Также для тех, кто верит в мистическую силу пирамиды стоит на нее приклеить натуральные камни, которые будут подходить под знак зодиака того, кому будет подарена данная фигура. В детском варианте пирамиду можно превратить в животное, приклеив к ней ушки, хвостик и нарисовать черты мордочки.
Способ 2
Такая схема пирамиды подразумевает использование готовой заготовки, которую можно скачать и распечатать на принтере. Этот вариант самый простой, так как не придется чертить фигуры самостоятельно. Главное подготовить все необходимые инструменты и оригинально украсить изделие на этапе декорирования.
Способ 3
Существует достаточно много советов, как сделать пирамиду из бумаги, определенная схема с размерами является неотъемлемой частью в выполнении оригами:
- Квадратный лист сложить, чтобы углы лежали противоположно друг к другу, лишнюю бумагу отрезать ножницами.
 Таким способом можно сделать ровный квадрат.
Таким способом можно сделать ровный квадрат. - Заготовку свернуть по одной диагонали, раскрыть и свернуть по другой и снова развернуть. Так намечаются нужные линии.
- Взять половинки квадрата, свернуть из него треугольник в два слоя. К центру свернуть два угла от основания. Аналогично повторить со второй стороны фигуры.
- Согнуть уголки к центру с одной стороны и с другой.
- Разогнуть ромб с каждой стороны, уголки его направить внутрь.
- Пирамиду нужно выгнуть так чтобы получилась звезда с четырьмя гранями. Фигуру взять двумя руками за разные концы и придать ей форму.
Постепенно придавая объекту форму, начнет получаться пирамида. Очень важно знать, что на последнем этапе нужно действовать аккуратно, стараясь не порвать случайно поделку.
Способ 4
Необходимые инструменты для поделки:
Выполнение:
- Вырезать квадрат. Согнуть заготовку пополам в разные стороны, чтобы образовались складки.
- Диагональ треугольника приложить к каждой из сторон квадрата и по сгибам сделать отметки.

- При помощи линий соединить треугольник с вершинами. Для точности рекомендуется использовать линейку.
- Отметить карандашом линии склейки сторон.
- Фигуру вырезать и нанести клей на линии склеивания.
Как сделать пирамиду из картона?
Сделать фигуру из картона своими руками можно быстро и просто. Использовать можно любую расцветку бумаги, но лучше всего подойдет цвет золота, бежевый, светло-коричневый.
Для того чтобы изделие выглядело более реалистично, то по бумажной заготовке можно произвести линии иголкой горизонтальные и вертикальные.
Благодаря этому будет создаваться эффект реальной мини-пирамиды из Гизы.
По вышеперечисленным пошаговым способам можно создать фигуру с гранями. Картонная пирамида делается по такому же принципу как из простой бумаги.
Но есть большой плюс, что ее можно украсить, например сахарным песком:
- Изделие можно покрыть полностью прозрачным клеем и нанести на него сахарный песок.
 Таким способом можно создать интересный сияющий эффект.
Таким способом можно создать интересный сияющий эффект. - Также пирамиду можно посыпать песком, предварительно обмазав ее клеем. Фигура приобретет эффект реалистичности.
«Золотое сечение» в пропорциях пирамиды
Эталон идеальной пирамиды – определенные правильные пропорции. Ключом к созданию правильной фигуры лежит коэффициент и цифры 7,23. Число, которое имеет значение в науке математике и геометрии, также эти цифры важны в архитектуре и даже медицине.
Отрезок длиной 7,23 нужно умножить на коэффициент 1,618. Полученное число 116, 981 следует округлить до 117 см. Эта длина является основанием пирамиды.
Также для получения больших моделей данное число можно умножать в несколько раз. Таким образом, длина нашей пирамиды получается 117 мм, а высота 72 мм.
По теореме Пифагора можно определить длину граней треугольника . Получится число 92,769, его нужно округлить до 93. Эти данные подстроены под идеальную пропорцию «Золотого сечения».
Как сделать развертку четырехугольной пирамиды?
Для изготовления четырехугольной фигуры потребуется:
- плотная бумага или картон,
- простой карандаш,
- линейка,
- ножницы,
- клей.

Этапы:
- Для начала нужно сделать выкройку, в которой основание будет 8 см, а высота 6,5 см.
- На листе бумаги нужно нарисовать ровный квадрат, отметить на каждой его грани середину.
- Провести из средних точек линии перпендикулярно квадрату, длиной 6,5 см — их всего должно получиться 4.
- Из каждой вершины провести по две линии к углам квадрата, так чтобы получились треугольники.
- Вырезать заготовку и сложить треугольники так чтобы они сошлись в единую вершину. Склеить фигуру.
Четырехугольную фигуру несложно изготовить самостоятельно. Также на основе этой пошаговой инструкции можно создавать пирамиды больше по размерам.
Как выполнить развертку правильной пирамиды?
Чтобы понимать как сделать пирамиду из бумаги, необходимо знать схему с размерами.
Если интересно как сделать пирамиду с разверткой из бумаги, существует не одна схема с размерами, которая поможет правильно выполнить фигуру. В момент проектирования развертки за основу берется правильный треугольник. Боковая поверхность представлена как плоский чертеж, состоящий из граней и многоугольника.
Боковая поверхность представлена как плоский чертеж, состоящий из граней и многоугольника.
Для начала определяется натуральная величина основания и истинная величина всех ребер (можно произвести при помощи циркуля). После того как три стороны были найдены строится основание и боковая грань. Берется произвольная точка и из нее проводится дуга равная длине боковых ребер заготовки. На дуге отмечаются четыре отрезка, равные основанию пирамиды.
Все линии соединяются, в том числе с произвольной точкой. К одному из получившихся треугольников пририсовывают квадрат, который равен основанию фигуры.
Сложные фигуры: объемные макеты
Фигуры такого типа делаются для получения навыков в работе с объемными изделиями из бумаги и в целях обучения детей начальным азам геометрии. Из таких моделей можно смастерить оригинальную подарочную упаковку. Иногда бывает сложно разработать правильную развертку, рекомендуется обладать хотя бы небольшими знаниями черчения.
Но существуют готовые трафареты, которые можно будет распечатать с принтера .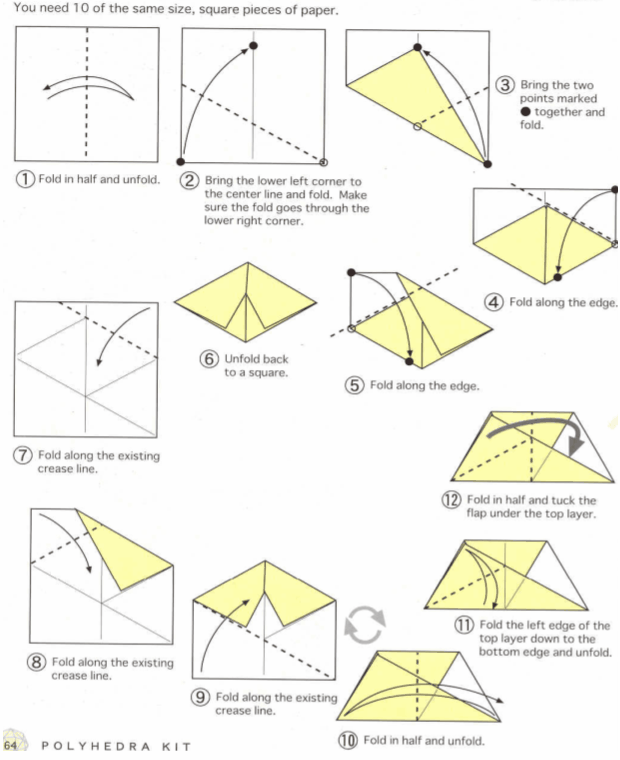 Макеты используются не только в развлекательных целях, но и в обучающих. Ребенку можно наглядно показывать, как выглядит та или иная фигура. Сложные модели могут быть: куб, октаэдр, додекаэдр, икосаэдр и другие.
Макеты используются не только в развлекательных целях, но и в обучающих. Ребенку можно наглядно показывать, как выглядит та или иная фигура. Сложные модели могут быть: куб, октаэдр, додекаэдр, икосаэдр и другие.
Перед тем как начать выполнять черчение фигуры стоит представить ее в 3D формате, сколько она имеет граней и измерений.
На листе бумаги нужно нарисовать грани, так чтобы они между собой правильно соединялись. У каждой фигуры есть свой определенный тип грани. Ребра тоже должны быть одинаковой длины, чтобы при скреплении не появились несостыковки. Если макет имеет одинаковые стороны, то в момент черчения можно нарисовать шаблон и по нему рисовать остальные заготовки.
3D макеты важны при обучении детей: они дают ученикам возможность подержать фигуры в руках, рассмотреть их и лучше понять строение. Также при изучении некоторых теорем (Эйлера) рекомендуется наглядное пособие.
Моделирование различных многогранников
Чтобы научиться выполнять более сложные модели, стоит начать с азов, например, с 3D треугольников. Постепенно улучшая навык в создании простых макетов можно приступить к сложным моделям. Сложные фигуры требуют навыков и отточенной сноровки при выполнении, например в момент развертки или придавания формы фигуре, нужно действовать так чтобы она случайно не порвалась.
Постепенно улучшая навык в создании простых макетов можно приступить к сложным моделям. Сложные фигуры требуют навыков и отточенной сноровки при выполнении, например в момент развертки или придавания формы фигуре, нужно действовать так чтобы она случайно не порвалась.
При выполнении чертежа следует внимательно наносить разметки и уметь рисовать фигуры.
Если есть вопрос, как сделать качественную пирамиду из бумаги, существует подробная схема с индивидуальными размерами. Стоит лишь приложить немного усилий, и тогда составит труда выполнить красивую и качественную работу, которая будет радовать глаз.
Благодаря вышеперечисленным способам можно легко создать различные макеты пирамид. Не сложно научиться выполнять эти техники, главное соблюдать все этапы постепенно и внимательно.
Видео о том, как сделать пирамиду из бумаги
Как сделать пирамиду из бумаги, узнайте в видео-ролике:
Схема выполнения объемной пирамиды:
Создавать поделки своими руками интересно не только детям, но и взрослым.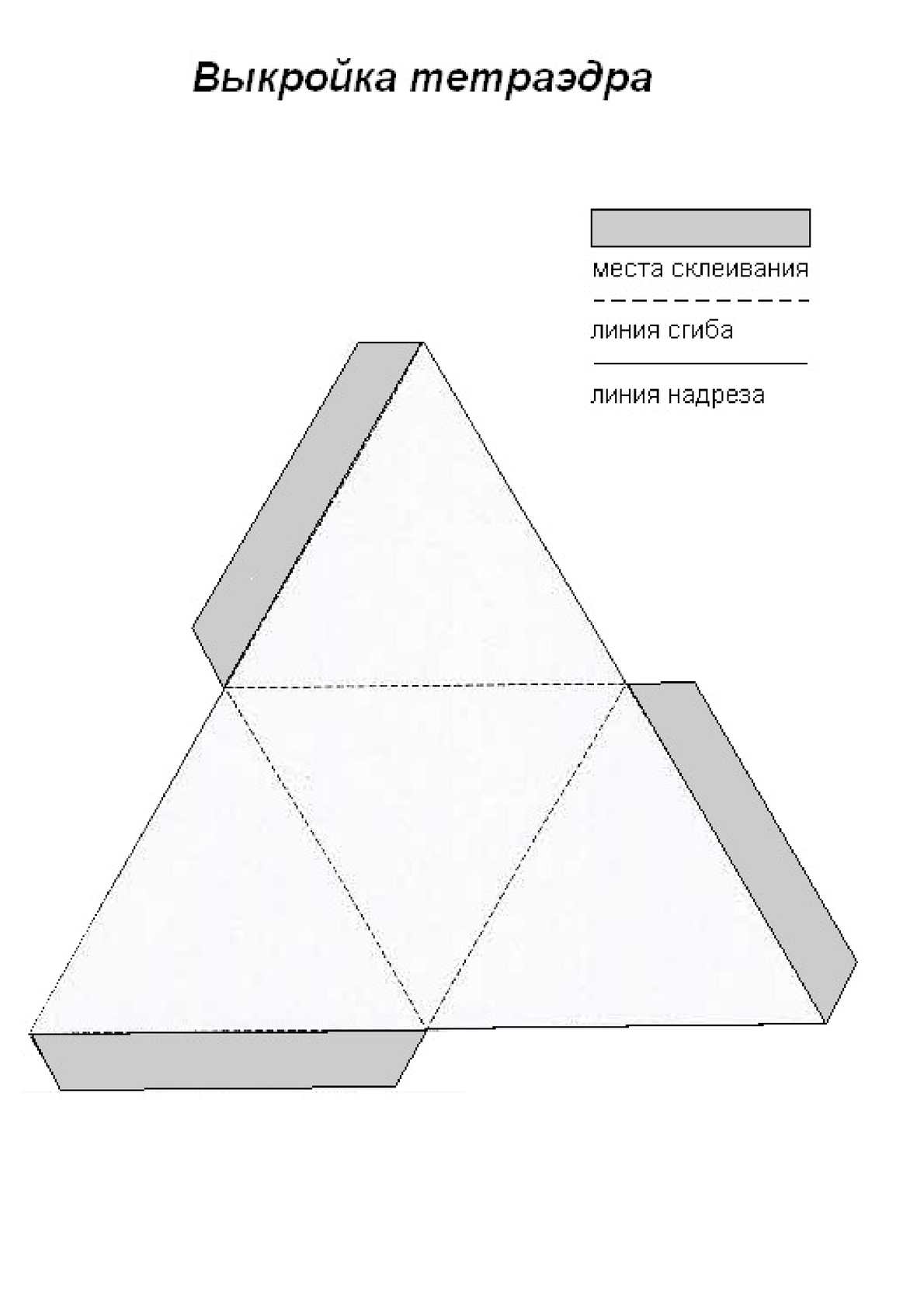 Однако для взрослых придумано достаточное количество моделей, которые отличаются сложностью выполнения и временем, затраченным на их создание. В последнее время у взрослых и детей появился интерес к созданию сложных геометрических фигур. К такому виду фигур относится икосаэдр, который представляет собой правильный многоугольник и является одним из платоновых тел – правильных многогранников. Эта фигура имеет 20 треугольных граней (равносторонних треугольников), 30 ребер и 12 вершин, которые являются местом стыка 5 ребер. Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда.
Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.
Однако для взрослых придумано достаточное количество моделей, которые отличаются сложностью выполнения и временем, затраченным на их создание. В последнее время у взрослых и детей появился интерес к созданию сложных геометрических фигур. К такому виду фигур относится икосаэдр, который представляет собой правильный многоугольник и является одним из платоновых тел – правильных многогранников. Эта фигура имеет 20 треугольных граней (равносторонних треугольников), 30 ребер и 12 вершин, которые являются местом стыка 5 ребер. Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда.
Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.
Предлагаем вам несколько вариантов разверток икосаэдра, которые можно распечатать, перенести на плотную бумагу и картон, согнуть по линиям и склеить.
Как сделать икосаэдр из бумаги: схема
Для того чтобы собрать икосаэдр из листа бумаги или картона, необходимо предварительно подготовить следующие материалы:
- макет икосаэдра;
- клей ПВА;
- ножницы;
- линейка.
Во время создания икосаэдра важно обратить особое внимание на процесс сгиба всех деталей: для того, чтобы ровно согнуть бумагу, можно использовать обычную линейку.
Примечательно, что икосаэдр можно встретить и в повседневной жизни. Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч. Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч.
Такой футбольный мяч можно сделать самостоятельно, распечатав предварительно развертку усеченного икосаэдра в 2 экземплярах:
Создание икосаэдра своими руками представляет интересный процесс, который требует вдумчивости, терпения и большого количества бумаги. Однако результат, полученный в итоге, будет радовать глаз еще долгое время. Икосаэдр можно дать поиграть ребенку, если он достиг уже трехлетнего возраста. Играя с такой сложной геометрической фигурой, он будет развивать не только образное мышление, пространственные навыки, но и знакомиться с миром геометрии. Если же взрослый решил создать икосаэдр самостоятельно, то такой творческий процесс по конструированию икосаэдра позволит скоротать время, а также похвастаться перед близкими своим умением создавать сложные фигуры.
Однако результат, полученный в итоге, будет радовать глаз еще долгое время. Икосаэдр можно дать поиграть ребенку, если он достиг уже трехлетнего возраста. Играя с такой сложной геометрической фигурой, он будет развивать не только образное мышление, пространственные навыки, но и знакомиться с миром геометрии. Если же взрослый решил создать икосаэдр самостоятельно, то такой творческий процесс по конструированию икосаэдра позволит скоротать время, а также похвастаться перед близкими своим умением создавать сложные фигуры.
Оригами – бумажные фигурки, которые относятся к японскому искусству и существуют в нём уже не одно столетие. Монахи ещё в древние времена, использовали фигурки из бумаги для декорации храмов и его залов, а также для применения их в религиозных целях (осуществление обрядов).
Сделать оригами из бумаги своими руками в состоянии каждый малоопытный мастер, но главным критерием есть имение усидчивости и точности движений. Сегодня вы поймёте, что не нужно быть асом, чтобы красиво сделать эти изделия.
Инструменты для оригами
Основное внимание стоит уделить выбору бумаги для поделок. Для оригами подойдёт офисная, твёрдая бумага разной цветовой гаммы. Она подойдёт для любых схем, как простых, так и сложных.
Для закрепления бумаги нужно приобрести клей-карандаш или клей ПВА. Подойдут и другие виды клея, лучшим вариантом будут те, что не оставляют следов, а если и оставили, то легко устраняются.
Приобретите краски в баллончиках, для придания необходимого оттенка изделиям с серой или обычной белой бумаги.
Для выравнивания краёв оригами подойдёт резак, только не стоит забывать про аккуратное поведение с ним.
Также для создания игрушек надо линейки, карандаши для черчения схем. Для придания креативности и необычности вашему оригами, можно украсить его с помощью бисера, стекляруса, стразами, ленточками.
Разновидности бумажных фигурок
Не считая классического вида, есть ещё много разных альтернативных видов:
- Классическое простое оригами – с него стоит начинать тем, кто впервые решил заняться бумажными фигурками.
 Примером данного стиля есть фигурка журавлика.
Примером данного стиля есть фигурка журавлика. - Оригами из модулей – сложнее чем первый вид. Несколько деталей (модулей) необходимо соединить простым складыванием. Изделие держится достаточно долго.
- Аэрогами – фигурки самолётов из бумаги.
- Киригами – создание фигурок происходит с использованием ножниц. Например, открытки.
- Кусудами – объёмное оригами, части изделия соединяются между собой с помощью нитей и клея. Форма фигурки часто напоминает большой шар. Данный вид часто использовался для украшений входа в храм.
Бумажный журавлик
Является классическим видом оригами. В народе ходит легенда, что если сделать тысячу журавликов, то сбудется то, что сердце хочет.
Подробно рассмотрим, как делать сделать эту чудесную фигурку.
- Согнув лист по диагонали, отрезаем ненужную бумагу, так чтобы остался лист напоминающий треугольник.
- Ещё раз сгибаем. Должно быть 2 треугольника. Из образовавшегося треугольника, расправляя делаем квадрат.
 Такую же процедуру проделываем и, с другой стороны.
Такую же процедуру проделываем и, с другой стороны. - Держим так, чтобы края были сверху, и загибаем их строго к центру.
- Верхний треугольник тоже сгибаем. И сразу расправляем сгиб, у нас получается контур.
- Уголок тот, что ниже остальных, загибаем горизонтально.
- Делаем ромб (слаживаем краешки к центру стороны). Проделываем те же маневры с другой стороной.
- Для формирования шеи, берёмся за нижнюю часть и начинаем загибать там, где внутренний контур. Таким же методом делаем журавлику хвост.
- Там, где находится шея, начало изгибаем, таким образом у нас получится клюв.
- Складываем ему крылья, воспользовавшись сгибанием на маленький угол.
При желании, журавля можно покрасить или сразу взять цветную бумагу. Оригами журавель готов.
Роза техникой оригами
Более привлекательными и легкими для большинства новичков, так и для мастеров оригами, являются цветы из оригами. Распространённой фигуркой является бумажная роза.
Рассмотрим пошаговую инструкцию и фото данного оригами:
- Берём цветную бумагу, желательно красного цвета, складываем пополам, потом ещё раз.
- Слой бумаги, что находится вверху, немного раскрываем так, чтобы у нас получился раздутый верх.
- Переворачиваем на другую сторону, и повторяем действие, что описаны в предыдущем пункте.
- Берём углы и загибаем их к верхнему уголку.
- Треугольник, что вскоре получился, сгибаем пополам, до появления контура.
- Раскрываем треугольник, потянув за оба угла вниз.
- Держа кармашки за верхнюю часть, загибаем вниз.
- Пункты с 4 по 7 проделываем и на другой стороне.
- Делаем загиб верхнего угла.
- Нижнюю часть разворачиваем как книгу.
- Выпучиваем так, чтобы получились 2 треугольника.
- Переворачиваем изделие.
- Правый нижний квадрат аккуратно сгибаем с верхнего в нижний край (строго по диагонали).
- Повернув на 180̊ и проделываем 13 пункт.
- Берёмся пальцами за стенки оригами, и не боясь крутим на 360̊, пока не увидим получившееся лепестки.

Бумажный лебедь
Данная техника более сложная, чем остальные так как здесь используется метод модульного оригами. Для того, чтобы сделать объёмного лебедя, нужно:
- Сделать приблизительно 460 треугольников с белой бумаги и 1 красный для клюва.
- Уголки двух треугольников вставляем в карманчик третьего.
- Прибавляем ещё два. Все уголки вкладываем в карман.
- Делаем три таких ряда. Необходимо взять около 30 модулей для каждого ряда. Закрываем круг.
- Вставляем заготовки для следующих двух рядов.
- Вдавливаем центр так, чтобы он потихоньку выворачивался.
- При всём этом края заворачиваем вверх.
- Делаем ряды дальше, но не забываем про шахматный порядок модулей.
- В 7 ряду делаем модули под крылья. Насаживаем 12 заготовок, сделав пропуск для 2 уголков, приделываем ещё такое же количество заготовок. На оставленных местах делаем лебедю хвост и шею.
- В 8 ряде для крыльев количество заготовок становится на 1 меньше.

- Так делаем и с последующими рядами, пока в последнем ряде не останется 1 модуль.
- Хвост делаем методом уменьшения на одну заготовок в каждом ряде.
- Шею собираем из 10-12 модулей, а голову из одной красной заготовки. Создаём шею, постепенно выгибая её.
- Когда шея готова, собираем её вместе с телом воедино.
Фото оригами своими руками
Обратите внимание!
Обратите внимание!
Как сделать макет призмы из бумаги. Как сделать геометрические фигуры из бумаги? Схемы и советы
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание.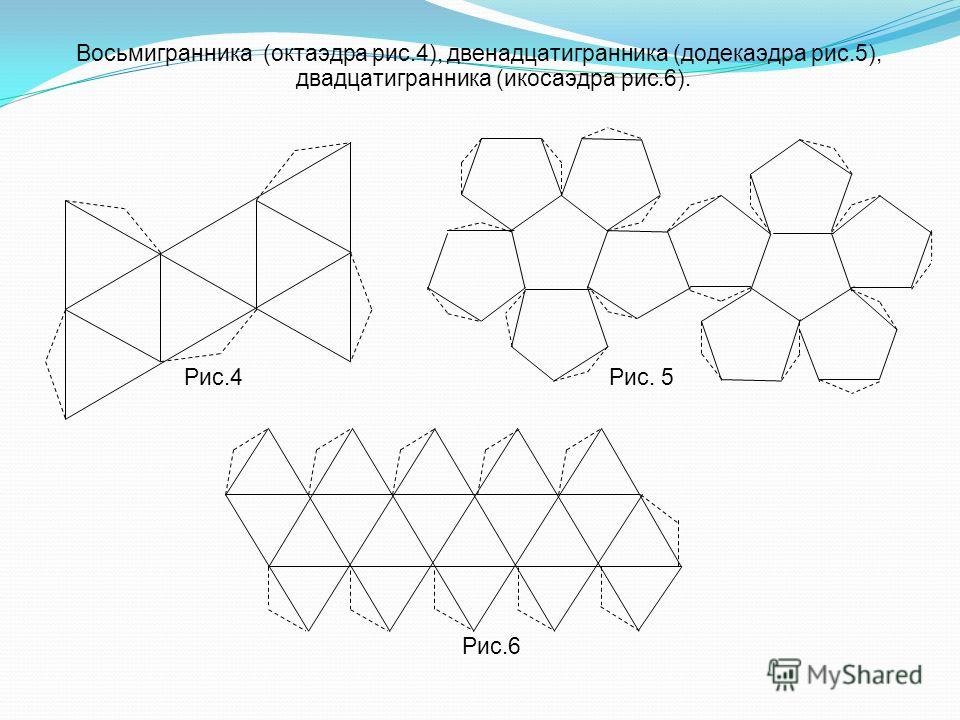 фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.

- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
- Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.

- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.

- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
Призма — это геометрическое тело, многогранник, основаниями которого являются равные многоугольники, а боковыми гранями — параллелограммы. Для непосвященного, возможно, это звучит несколько устрашающе. И, когда вашему ребенку на урок геометрии надо принести призму, собственноручно изготовленную дома, вы пребываете в растерянности, не зная как помочь своему любимому чаду. На самом деле все не так уж и сложно и, воспользовавшись нашими советами, как сделать призму, вы достойно справитесь с этой проблемой.
Как сделать призму из бумаги
Сразу условимся, что делать мы будем прямую призму, то есть призму, у которой боковые ребра будут перпендикулярны основаниям. Сделать же наклонную призму из бумаги весьма проблематично (подобные макеты обычно выполняются из проволоки).
Мы уже знаем, что в основаниях призмы лежат два одинаковых многоугольника. Поэтому нашу работу начнем именно с них. Простейший из многоугольников – треугольник. Значит, и призму сначала будем делать треугольную.
Как сделать треугольную призму
Нам понадобится плотная белая бумага для черчения, карандаш, транспортир, циркуль, линейка, ножницы и клей.
Чертим треугольник, можно любой, но чтобы наша призма получилась особенно красивой, треугольник сделаем равносторонний. Такая призма в геометрии называется «правильная». Выбираем на свое усмотрение величину стороны треугольника, допустим 10 см. Линейкой откладываем этот отрезок на бумаге и транспортиром отмеряем угол в 60 ∗ от одного конца нашего отрезка.
Проводим наклонную линию. На ней при помощи линейки откладываем 10 см от конца отрезка. Таким образом, мы нашли третью вершину треугольника. Соединяем эту точку с концами начального отрезка и равносторонний треугольник готов. Его можно вырезать. Аналогично делаем второй треугольник, или аккуратно обводим на бумаге контуры первого. Ну вот, два основания у нас уже есть.
Делаем боковые грани. Решаем, какая у призмы будет высота. Допустим, 20 см. Чертим прямоугольник, у которого величина одной стороны это высота призмы (в нашем случае – 20 см), а вторая сторона равна величине стороны основания, умноженной на количество этих сторон (у нас: 10 см х 3 = 30 см).
На длинных сторонах делаем отметки через каждые 10 см. Соединяем противоположные отметки прямыми линиями. По ним потом надо будет аккуратно согнуть бумагу. Это — боковые ребра нашей призмы. Намечаем узкие припуски для склеивания по двум длинным и одной короткой стороне прямоугольника (достаточно полосок шириной 1 см). Вырезаем прямоугольник вместе с припусками, аккуратно отгибаем их по разметке. Сгибаем ребра.
Вырезаем прямоугольник вместе с припусками, аккуратно отгибаем их по разметке. Сгибаем ребра.
Начинаем сборку. Склеиваем прямоугольник по боковой грани в трубу треугольного сечения. Сверху и снизу на отогнутые припуски наклеиваем треугольники-основания. Призма готова.
Вдаваться в подробности вопроса как сделать призму из картона, пожалуй, не стоит. Весь алгоритм сборки остается таким же, только бумагу замените тонким картоном. Меняя количество сторон у многоугольников основания, вы теперь самостоятельно сможете сделать и пяти- и шестиугольную призму.
В основе геометрического тела – призмы лежат многоугольники, а каждая боковая грань – параллелограмм. Непосвященный, возможно, немного испугался. Но если вашего ребенка просят прийти на урок с призмой, вы, естественно, захотите помочь ему и объяснить, как сделать призму из бумаги.
Начнем с изготовления прямой призмы. В этой призме боковые ребра перпендикулярны основаниям. Наиболее проста в изготовлении своими руками призма из бумаги с тремя гранями, так как в ее основаниях лежат простейшие из многоугольников – треугольники. Изготовим «правильную» призму. У нее основания представлены равносторонними треугольниками.
Изготовим «правильную» призму. У нее основания представлены равносторонними треугольниками.
Продумаем, какая по высоте будет наша треугольная призма из бумаги. Начертим прямоугольник-с одной стороной, равной высоте, а другой — равной длине периметру треугольника в основании. Полученный прямоугольник разделим параллельными прямыми на три равные части. От углов прямоугольника, находящегося в середине, циркулем проведем окружности с радиусом, равным стороне нашего треугольника в основании. Где окружности пересекутся за пределами первоначального прямоугольника, поставим точки и соединим их с центрами окружностей. Мы должны получить фигуру, изображенную в середине рисунка. Далее фигуру вырезаем с небольшими припусками для склеивания, сгибаем по имеющимся прямым линиям и получаем готовую призму.
По какому шаблону изготавливается призма из бумаги с четырьмя гранями, наглядно демонстрирует схема на рисунке.
Шестиугольная призмаПример заготовки для пятигранной призмы представлен на рисунке. Здесь высота пирамиды 10 см, длина сторон у пятигранника в основании по 3 см. Похожим образом может быть изготовлена шестиугольная призма из бумаги, но в ее основании лежит шестиугольник.
Здесь высота пирамиды 10 см, длина сторон у пятигранника в основании по 3 см. Похожим образом может быть изготовлена шестиугольная призма из бумаги, но в ее основании лежит шестиугольник.
Наклонная призма из бумаги представлена на этом рисунке. Ее боковые грани находятся под углом к основанию. Такую призму можно изготовить по шаблону-развертке.
Прямоугольник, квадрат, треугольник, трапеция и другие — геометрические фигуры из раздела точной науки. Пирамида — это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии.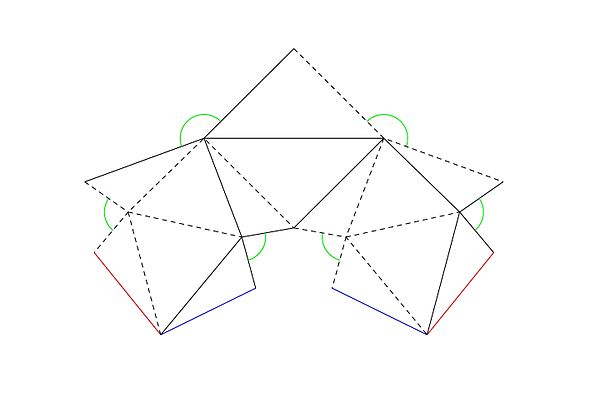 Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
Материалы и приспособления
Моделирование и выполнение многогранных объемных геометрических фигур — интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:
- бумага или картон;
- ножницы;
- карандаш;
- линейка;
- циркуль;
- ластик;
- клей.
Определение параметров
Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной
Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием а ее вершина спроецирована в его центр. В качестве основания выбран Данное условие определяет название. Боковые ребра у пирамиды — это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.
Боковые ребра у пирамиды — это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.
Как выполняется развертка правильной пирамиды?
Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае — это треугольная пирамида. Определяем размеры выбранной фигуры.
Чтобы построить развертку пирамиды, основанием которой является правильный треугольник, в центре листа, используя линейку и карандаш, нарисуем основание заданных размеров. Далее к каждой его стороне вычерчиваем боковые грани пирамиды — треугольники. Теперь переходим к их построению. Размеры сторон треугольников боковой поверхности измеряем циркулем. Ножку циркуля ставим в вершину нарисованного основания и делаем засечку. Действие повторяем, перемещаясь в следующую точку треугольника. Пересечение, полученное в результате таких действий, определит вершины боковых граней пирамиды. Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.
Далее к каждой его стороне вычерчиваем боковые грани пирамиды — треугольники. Теперь переходим к их построению. Размеры сторон треугольников боковой поверхности измеряем циркулем. Ножку циркуля ставим в вершину нарисованного основания и делаем засечку. Действие повторяем, перемещаясь в следующую точку треугольника. Пересечение, полученное в результате таких действий, определит вершины боковых граней пирамиды. Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.
Сборка макета
Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.
Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник.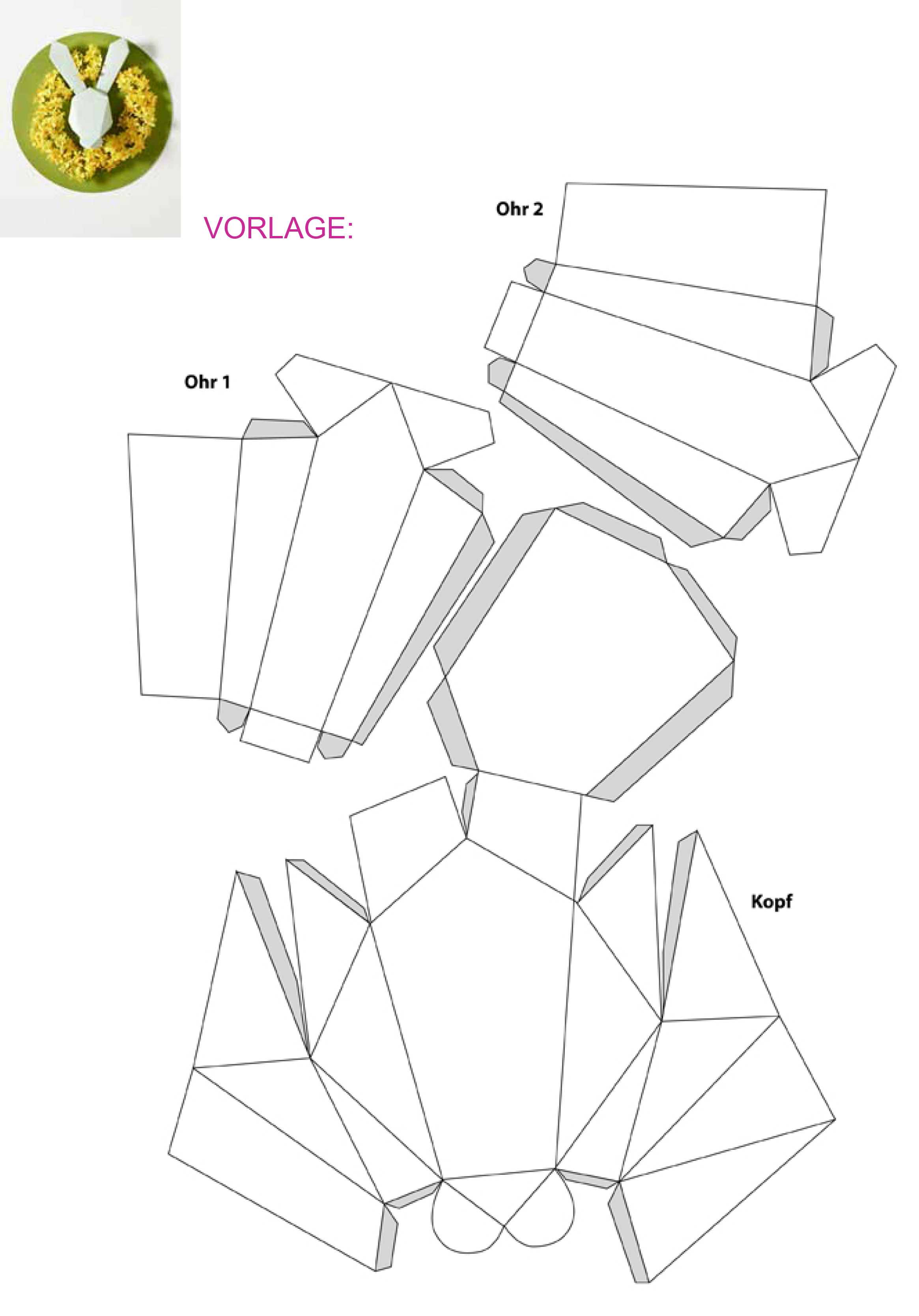 Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.
Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.
Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.
Завершающий этап выполнения макета
Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.
Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.
Объемные макеты сложных фигур
После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани — это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.
Построение чертежа
Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями — подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим которой будет измеренное расстояние.
Следующий этап — это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники — квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.
Завершение моделирования
Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.
Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.
Изготовление разных моделей многогранников
Выполнение объемных моделей геометрических фигур — увлекательное занятие. Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.
Вы достигли в этом мастерства и ваша пирамида из бумаги готова. Самая узнаваемая геометрическая фигура – это пирамида. Нужно будет из бумаги вырезать одну фигурку и потом соединять все элементы, чтобы получилась пирамида. Из этой статьи, благодаря описаниям, картинкам и видео вы узнаете о нескольких способах, как сделать из бумаги пирамиду.
Вплотную к созданию моделей многогранников из бумаги примыкает искусство кусудамы, т.е. создание красивых цветных шаров из бумаги. В 2011 году издательство «Многогранники» поставило изготовление многогранников из бумаги на надежные коммерческие рельсы. Следует отметить отлично оформленный сайт, содержащий фотографии готовых моделей, видеоинструкции по их изготовлению (конечно, только из соответствующих наборов) и другие материалы.
Пирамида – это в первую очередь геометрическая фигура, а потом все остальное. По числу углов основания бывают следующие пирамиды треугольные, четырёхугольные и т. д. Пирамида это частный случай конуса. Пирамида, как и другие многогранники, были известны с древних времен и имеет богатую историю.
Евклид называет пирамиду телесной фигурой, которая ограничивается плоскостями, от одной плоскости, т. е. основания и сходятся в одной точке, т. е. вершине. Первое письменное толкование термина «пирамида» появилось в Европе в 1555 году. И имело следующие значение «это один из видов самых древних сооружений королей».
В современном Египте «пирамида» – является собирательным образом, у каждой из пирамид есть свое имя: пирамида Хеопса, пирамида Хефрена и т.д. Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Благодаря искусству оригами можно создать и пирамиду. Для поделки нужно взять: лист, из которого делается модель пирамиды; небольшой треугольник; клей; ножницы; маркер. Затем линиями соедините нарисованный треугольник и вершины будущей пирамиды.
Радужную окраску изображения, даваемого линзой, наблюдали, конечно, и до него. Было замечено также, что радужные края имеют предметы, рассматриваемые через призму. Падая на стеклянную призму, он преломлялся и давал на противоположной стене удлиненное изображение с радужным чередованием цветов. Рис. I. Схема разложения белого света с помощью призмы.
Даже беглый взгляд на галерею многогранников доказывает, что звёздчатые многогранники являются очень красивыми и декоративными. Затем вводится понятие звездчатых форм, трехмерный калейдоскоп, анализируются принципы построения звездоформ и рассматриваются соответствующие бумажные модели.
В нашей стране весомый вклад в изготовление и популяризацию бумажных моделей многогранников внесла Гончар Валентина Васильевна, архитектор и руководитель кружка бумажного моделирования. Её книги «Кристаллы» (1994) и «Модели многогранников» (1997, 2010) посвящены в основном платоновым и архимедовым телам, а также их отдельным звездчатым формам.
Другое направление, развитое Валентиной Васильевной — создание моделей многогранников в технике оригами (в идеале, без использования клея и ножниц). Ею создан «универсальный модуль оригами», складывая который можно получать отдельные звездчатые многогранники, и даже делать оригинальные подвижные модели — трансформеры. Каждый набор посвящен конкретному многограннику и содержит вырезанные и подогнанные детали, а также инструкции по изготовлению.
Развертка и схема пирамиды. Как сделать пирамиду из бумаги самому
И всякий раз, когда смежные грани окрашиваются в одинаковый цвет, можно упростить изготовление модели, уменьшив количество заготовок и клеевых соединений. Впрочем, зачастую упрощенно раскрашенные или даже одноцветные бумажные модели многогранников весьма эффектны.
Согласитесь, вы намного быстрее догадаетесь, о чем идет речь, если услышите слово «пирамида». Услышав же слова додекаэдр, тетраэдр, гексаэдр, октаэдр или икосаэдр призадумаетесь, и будете вспоминать, как они выглядят и что из себя представляют.
Слово пирамида имеет много значений. Еще в Древней Греции словом «пирамис» называли пшеничный пирог, напоминавший форму египетских пирамид. Затем это слово стало означать сложный термин «монументальную структуру имеющая квадратную площадь в основании с наклонными сторонами, встречающимися на вершине». Начало геометрии пирамиды было положено в Древнем Египет и Вавилоне, хотя самое активное развитие оно получило в Древней Греции.
Пирамида в данном случае делается из квадратного листа бумаги путем некоторых действий. Постепенно из бумаги начнет проявляться пирамиду, которую мы так хотели собрать. После прочтения книги Веннинджера вы научитесь самостоятельно проектировать новые звездчатые формы и изготавливать их модели из бумаги. В книге приводятся трафареты и шаблоны для вырезания из бумаги составных частей будущей модели (заготовок), а также даются схемы соединения частей между собой и таблицы раскраски.
Схема пятиугольной пирамиды. Пирамидка оригами – модель из купюры своими руками
Первый способ, как сделать пирамиду из бумаги.
1. Первым делом мы делаем сгибы руками. Для этого согните и разогните листок пополам, по вертикали, по горизонтали и по диагонали. Линии сгиба отмечены на картинке сплошными тонкими линиями. Затем согните уголки к центру, линия сгиба указана пунктиром.
2. Положите листок как указано на фото. Загните правый и левый угол к верхнему. Пунктиром обозначены линии сгиба. Далее расправляем верхний угол должен получиться квадрат.
3 . Сделайте сгибы верхнего квадрата, по линиям показанным на схеме. Они нам понадобятся для того чтобы ровнее заправить углы. Затем своими руками заправляем эти уголки во внутрь.
4 . Отогните верхний угол, затем поверните деталь на 180 градусов.
5 . С этой стороной проделываем всю ту же работу что описаны 3 и 4 шагах.
6 . Получим вот такую деталь. Поднимаем углы к верху
7 . Расправляем боковые углы. Тем самым выпрямляем дно нашей фигуры. Вот мы и подходим к завершению. Пирамида из бумаги практически готова.
8 . В завершении проглаживаем руками ребра дна пирамиды.
В принципе наша пирамида готова. В нее можно запаковать небольшой подарочек. Для этого необходимо сделать дыроколом отверстия в вершинах и продернуть через нее красивую веревочку. Будет очень красиво смотреться на елочке.
Наглядное видео, мастер класс по изготовлению оригами выше описанной фигуры.
Второй способ как сделать пирамиду из бумаги.
Данный вариант пирамиды чуть посложнее чем первый, вам потребуется побольше времени и терпения. Но зато результат получается очень необычный.
Нам понадобится 4 цветных листочка размером примерно 15 на 15 сантиметров.
1. Возьмите один лист и положите его цветной стороной вниз. Затем согните его пополам по вертикали, по горизонтали и разверните обратно.
2 . Низ листочка загните по центральной линии сгиба, затем разверните обратно.
3 . Загибаем нижний край наверх. Место сгиба обозначено пунктиром.
4 . Должно получиться вот так
5
. Складываем получившуюся фигуру пополам, примерное место сгиба обозначено на фото.
6 . Переворачиваем цветной стороной вверх.
7
. Загибаем левую и правую часть к центральной линии и разгибаем обратно.
8 . Загибаем лист по пунктирной линии.
9
. Загибаем подобным образом еще один угол.
10. Должно получиться вот так.
11. Далее нам нужно загнуть угол так что бы точки В и С соединились.
12. Вот что должно получиться
13. Сгибаем по пунктиру наверх.
14. Одна из четырех заготовок готова.
15. Все тоже самое делаем с тремя другими листочками. В результате получим 4 одинаковых фигуры. Они и будут являться сторонами нашей пирамиды.
16. Соединяем их друг с другом как указанно на фото.
Поздравляю вы справились с заданием. Вот так просто можно своими руками сделать необычную модель пирамиды.
Если у вас не получилось сделать какой-либо шаг, смотрите внимательно видео и пробуйте снова.
Шаблоны и макеты пирамиды для распечатки.
Данные шаблоны вы сможете распечатать на картоне, вырезать своими руками и склеить. Части фигуры заштрихованные или обозначены темным цветом точками необходимо проклеить во внутрь. Советуем вам линии сгиба проглаживать по линейке тупым предметом. Так ваша модель получится более ровно. После изготовления проявите фантазию и украсьте пирамиду цветными лентами. Так же можете разукрасить ее цветными карандашами и фломастерами. Поэкспериментируйте своими идеями для получения восхитительного результата.
Развертка пирамиды — очень быстрый и легкий способ изготовления своими руками. Готовое изделие своим видом напоминает египетское чудо света.
Можете посмотреть наш видео урок, по изготовлению фигуры по шаблону.
Встретилась мне вот такая интересная статья про пирамиды, решила поделиться.
«Здесь мы поговорим о простом и удобном способе в изготовлении портативной модели Пирамиды в пропорциях «золотого сечения».
Делаем портативную пирамиду «золотого сечения»
Более 4 лет я делал не очень большие пирамидки в пропорциях «золотого сечения» (размер которых я обосновал исходя из знания о длине волны нашего материального мира, равной 7,23см) и они за это время очень хорошо себя зарекомендовали, даже не смотря на столь миниатюрный вид. Давайте с них и начнём.
Итак, мы будем делать, так называемую, классическую форму Пирамиды, очень похожую по своему виду на форму самых известных Пирамид на Планете – Египетских пирамид.
Но как я и сказал, что для своих расчетов нам потребуется знание первичной величины – 72,3 мм. Я применяю это значение для расчётов всех последующих размеров Пирамид и объясняю это простой логикой. Если длина волны нашего трёхмерного мира равна 7,23см, то для того, что бы Пирамида как объект этого живого пространства вошла в гармоничный резонанс и сонастрой с энергиями этого мира, нужно учитывать эту величину в качестве базисной единицы геометрической размерности модели Пирамиды.
Для тех, кто хочет более подробно узнать о числе 7,23 см, читайте книгу «Древняя тайна Цветка Жизни», глава вторая (2), хотя я пришёл к этому числу из своих духовных поисков и анализа тайных законов нашего дуального мира.
Следующая операция необходима для приведения геометрии Пирамиды к эталону «золотого сечения». И для этого нам нужно знать коэффициент «золотого сечения», который и считается ключом к пониманию божественной гармонии жизни. Это известное число во многих науках от математики и геометрии, до архитектуры и медицины, с ним связаны не только все основные загадки в геометрии Египетских Пирамид, но и многие параметры в работе сердца и биоритмов человека.
Итак, мы имеем отрезок длины и коэффициент 1,618.
При умножении 72,3 мм на коэффициент 1,618 у нас получается размер 116, 981 мм, поэтому мы округляем данное значение до 117 мм. Это и будет принято за размер длины в основании Пирамиды или размер основания треугольника необходимого для изготовления стороны Пирамиды.
Если же вам мало этой длины, умножьте число 116,981 снова на 1,618 и получите размер длины для модели с большими размерами.
Ну а мы продолжаем работать с этими числами 72,3 мм и 117 мм.
Для нашей Пирамиды с геометрией классической формы будем иметь следующее: высота Пирамиды 72 мм, длина основания Пирамиды 117 мм.
Чтобы нам сделать геометрическую развёртку деталей для нашей модели Пирамиды, нам необходимо узнать размеры треугольных граней, из которых и будет собираться данная Пирамида. Один размер нам уже известен это длина основания Пирамиды, равная 117 мм.
Зная закон Пифагора, мы быстро найдём апофему Пирамиды. Нам нужна высота Пирамиды и половина длины основания Пирамиды.
По формуле Пифагора получаем число 92,769 и округляем его до 93 мм.
Вот мы и имеем всё, что нам надо для быстрого, и приближенного к эталону классической формы, построения портативной модели Пирамиды. Наша модель будет состоять из следующих деталей: четыре треугольника с размерами 117 мм (основание треугольника) и 93 мм (высота треугольника), в варианте полой Пирамиды. И плюс квадрат основания Пирамиды с размерами 117 мм на 117 мм, в случае, если нашей модели понадобится делать дно.
А далее берёмся за линейку, ручку и материал из которого и будет сделана наша мини-пирамида. У всех давно на слуху, что лучше Пирамиды делать из диэлектрических материалов (картон, фанера, ДВП, пластик, стекло и т.п.).
Не будем и мы уходить от этой традиции, хотя от себя поясню следующее: пирамиды можно делать из разных материалов и даже из токопроводящих, т.е. из металлических, но стоит правильно понимать природу такого изготовления, а она заключается в том, что пирамида по максимуму должна быть однородной, как в своей геометрии, так и в материале конструкции. Если это дерево, то вся из дерева или в сочетании с диэлектриками. Если это металл, то вся из металла. Не желательны точечные крепления на основе шурупов, гвоздей и болтов, особенно если основной материал в конструкции – диэлектрик, т.к. эти точечные крепления будут создавать иную природу полей, относительно общего поля Пирамиды, что и будет создавать «шумовые всплески» в энергетике такой Пирамиды.
На нашем куске рабочего материала (в моём случае это пластик) делаем разметку деталей, — сперва, отмерив размер 93 мм, для высоты треугольников, и затем 117 мм для отрисовки треугольников с учётом длины основания. Вся схема понятна в фото-приложении.
И в таком порядке размечаем все четыре размера треугольных граней. А далее берёмся за инструмент, — кто за ножницы, если это картон, а кто за нож для пластиков или пилу, в случае фанеры или ДВП.
Через минуту-другую и вас должны получиться четыре идентичные треугольника, которые и послужат нам для склейки объёмной фигуры Пирамиды.
Но если у вас был толстый материал, то понадобится ещё затратить время на снятие боковых фасок для точного соединения прилегающих граней в треугольниках.
Тут можно пойти несколькими путями, либо снова браться за основы геометрии и вычислять угловые значения, а потом делить угол пополам, и уже взяв его как шаблон, отстраивать инструмент под снятие фаски, либо идти опытным путём и, сперва, снять чуть-чуть фаску по граням, а потом приложить треугольники для проверки. И так за пару заходов вы сделаете довольно точную подгонку деталей. В итоге у вас должно всё сходиться в точку при вершине Пирамиды, это будет качественная работа.
Так же надо снять фаску и при основании треугольников, для прилегания Пирамиды по горизонту, но здесь уже будет несколько иной угол. Хотя смотрите сами, даже без этого Пирамида будет уже решённой.
Подходим к сборке и проклейке деталей нашей Пирамиды. Для этого нужно аккуратно разложить все треугольники на столе и сложить их грань к грани, так чтобы образовалась Пирамида в развёртке на плоскости. И с внешней стороны скрепить края смежных треугольников, к примеру, скотчем, самоклеющей бумагой или проклеенными отрезками бумаги. И уже на этапе последнего треугольника можно приподнять собранную модель, так чтобы треугольники касались основаниями стола, а сама развёртка свернулась в Пирамиду, образовывая объёмную модель. Тут то и надо точно склеить первую и четвёртую грани, совмещая точки углов при вершине и при основании Пирамиды. Если ваша фигура получилась устойчивой, то переверните Пирамиду и, имея доступ во внутрь, пройдитесь по швам и заполните их клеем. После этого ещё раз проверьте, что бы сохранился квадрат основания, и дайте время схватиться клею.
На этом этапе у нас получится полая модель пирамиды и этого для многих будет достаточно, т.к. именно имея доступ в подкупольную зону Пирамиды, вы сможете более эффективно работать с ней.
В случае, когда вы хотите иметь Пирамиду с закрытым дном, следует заняться подготовкой основания Пирамиды с размером 117 на 117 мм и последующей склейкой купола Пирамиды с квадратом основания.
Когда клей на швах Пирамиды полностью затвердеет, можно аккуратно снять наложенные ранее кусочки клеевого скотча на стыках граней и теперь ваша Пирамида будет крепкой и целостной.
Представьте, что у нас есть источник энергии, силового поля или потока света, это уже хорошо само по себе, но данное поле имеет очень широкий спектр воздействия, а нам нужна всё же некая целевая задача в работе этой силы и нам нужно информационно адаптировать этот поток под себя, т.е. наложить некую полезную структуру.
Иными слова, представьте, что Пирамида это некий аналог фильмоскопа, т.е. в ней создаются определённые поля вращения, как световой поток внутри фильмоскопа. И наша задача наложить полезную информацию на данное поле, точно также как в проекторе происходит наложение картинок на световой поток. Пирамида даёт поле благотворного воздействия, а задача мастера состоит в том, чтобы направить это поле на решение более конкретных задач. И для этого мы должны больше узнать о цветотерпии и энерго-информационном воздействии на симпатическую и психическую природу человека.
Целители, учёные, медики и люди, занимающиеся духовными практиками, давно и успешно применяют и знают о положительном воздействии на человека, его настроение и здоровье цветовых вибраций и особых энергетических знаков, матриц, мандал и пантаклей. Цвет вызывает усиление тех или иных процессов как на тонко-вибрационном плане ауры человека, так и на физическом плане в работе его органов и систем. Поэтому, когда вы имеете источник силы в виде действующей Пирамиды «золотого сечения», то будет очень правильно придать её внешним качествам определённую информационную программу, настроенную на приятное для вас восприятие.
Это может быть определённый цвет вашей Пирамиды; аппликации или узоры сделанные вами на гранях; просто наклеенное фото или цветок, вырезанные из журнала; добрые пожелания для себя или в адрес близкого человека, написанные от руки, либо в ином виде, но главное с любовью и от души; маленькая иконка святого или Архангела и лучше, если это будет в круге; молитва, веление, стих, всё, что близко и дорого вам по силе Веры и своим устремлениям к добру. Теперь вы здесь творец своего будущего и магия добра (в понимании закона), сейчас полностью в ваших руках и светлых мыслях.
Творите и окутывайте идеями и мысле-формами свою Пирамиду, ведь она имеет закон четвёртого измерения и поэтому является связующим звеном и проводником в более высокие октавы жизни.
А для тех, кто уже не так молод, но полон желания жить, ещё и ещё, я посоветую очень верный метод. Относите его к магии, смотрите на это как на самовнушение, верьте или не верьте, или знайте и верьте, а ещё лучше изучите работы по волновой генетике, и тогда узнаете и поверите, что информацию можно переносить при помощи света, вибраций и тонких полей мысли, любви и намерения. Этот метод можно отнести к области ювенологии – науки о сохранении и продлении молодости. Он прост, но очень эффективен!
Вам нужно выбрать ряд фотографий или рисованных портретов, где вы были молоды, красивы и жизнерадостны. Далее, взять свой источник силы – Пирамиду, и разместить на её гранях понравившиеся вам фото или хотя бы одно фото на одной грани. А далее нужно выставить свою Пирамиду по сторонам света и попробовать в расслабленном состоянии всмотреться в своё юное лицо и вспомнить, как хорошо быть молодым и как вы были счастливы в то время. В это время, благодаря вашей совместной работе с Пирамидой, будет происходить перенос информации о вашем юном состоянии, а Пирамида будет заряжать уже вас этой энергией. Но ещё более правильно, если вы начнёте заряжать питьевую воду при помощи своей «омолаживающей» Пирамиды.
Для этого нужно взять стакан или банку наполненные водой и накрыть их куполом Пирамиды, при этом выставив её по сторонам света. Такая вода будет обладать целым рядом полезных свойств, включая и информацию о вашей юности, считанную с фотографии и ваших эмоциональных воспоминаний.
Пейте на здоровье и укрепляйте свои силы, здоровье и дух. Надеюсь, ваша вера, мечты, надежды и фантазия помогут сделать этот метод и свою Пирамиду ещё более полезными, жизнеутверждающими и волшебными. Я вас люблю и желаю всем добра и мира!»
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
- Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Из бумаги
Из картона
Развертки куба
Треугольника
Прямоугольника
Цилиндра
Ромба
Призмы
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Конуса
Пирамиды
Шестигранника
Макета с припусками
Параллелепипеда
Трапеции
Овала
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
Многогранника
Параллелограмма
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
Сложных фигур
3d
Октаэдра
Тетраэдра
Икосаэдра
Додекаэдра
Гексаэдра
Фигурок из треугольников
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.
На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.
Основные ошибки при работе с моделями:
- Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.
Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура — ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Геометрические фигуры из картона своими руками схемы — Bitbucket
———————————————————
>>> СКАЧАТЬ ФАЙЛ <<<
———————————————————
Проверено, вирусов нет!
———————————————————
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Как сделать объемные геометрические фигуры из бумаги (схемы, шаблоны )?. Развивающие игрушки своими руками — сортер Геометрические фигуры. Как научиться делать объемные фигуры из бумаги и картона?. если это разноцветные геометрические тела оригами, сделанные своими руками. Нужно склеить несколько геометрических фигур? Скачайте развертки. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂 Развёртка. Дракончик схема вязания. В год Дракона. своими руками из бумаги и картона фото видеоролики игрушки это интересно новый год схемы радиотехника развёртки из дерева самоделки подарки. Как сделать своими руками геометрическую фигуру треугольной пирамиды из листа бумаги формата А4. Предложенная схема по оригами полностью исключает применение. 9:29. Поделки из бумаги Додекаэдр оригами — Duration: 5:25. Своими руками 66,279 views · · Dwunastościan (dodekaedr) — origami. Объемные геометрические тела из бумаги своими руками. Схемы. Предложите ребенку угадать, какая фигура получится из определенной развертки. Об искусстве складывания из бумаги. Азбука. **Оригами схема объемного куба. Такой вариант геометрической фигуры получил название икосаэдр. Геометрические фигуры из бумаги покоряют четкостью, даже строгостью. можно создать своими руками удивительный декор для дома. Объемные геометрические фигуры из бумаги — делаем из бумаги или картона разные геометрические фигуры, например, чтобы и заниматься с меленькими детьми или на. Подарок — 3d цветок своими руками. Как сделать танграм своими руками. называют геометрическими конструкторами , головоломками из картона или. Схемы и фигуры игры танграм. Делаем из бумаги простые фигуры: куб, пирамиду, призму, параллелепипед и др. Как нарисовать развертку? Готовые схемы — распечатай и склей. Как самому сделать макет геометрических фигур. Макет конуса, макет цилиндра, макет куба склеить из бумаги. Чертежи макетов, для самостоятельной. Геометрические фигуры из бумаги своими руками схемы — Генератор свободной энергии тесла своими руками, Обшивка стен пластиковыми панелями. Об изготовление своими руками моделей многогранников из бумаги. а также даются схемы соединения частей между собой и таблицы раскраски. Нарисуйте на картоне ровные буквы, геометрические фигуры или узоры и вырежьте их. Поделки из картона своими руками: геометрическая лампа. Настенная декорация из картона своими руками (схема). 4. Человеческие фигуры из бумаги в технике папье маше. В этом мастер классе хочу предложить вам схему симпатичных ажурных шаров из бумаги. Делаем интересные поделки из салфеток,а также — оригами. Тем не менее, в основе фигур могут лежать и другие геометрические фигуры. Схема для начинающих. Поделки из бумаги в технике оригами. А вообще, если говорить о пирамиде – то это загадочная фигура. Сделать из бумаги своими руками!. вырезав из бумаги соответствующие фигуры и собрав ее), так и очень сложные (например, из простого листа. Двумя руками возьмитесь за разные концы и фигуре придавайте объем. Метки: развитие ребенка детям алфавит счет геометрические фигуры. самостоятельно при наличии ножниц, принтера, бумаги и хорошего клея. Читать далее. Метки: декор своими руками развертка геометрические фигуры. бисер брошь жгут колье цветосочетание Схемы геометрические фигуры жук.
Новый алгоритм создает прочные узоры оригами для любой трехмерной формы
Новый алгоритм, основанный на более ранней, более слабой версии, моделирует 3D-поверхности как маленькие плоские грани и отображает их на плоской поверхности для создания сложного «рисунка складок».
В 1999 году профессор Эрик Демейн, специалист по информатике из Массачусетского технологического института, опубликовал влиятельную статью по вычислительному оригами. В нем описан алгоритм, который теоретически может создавать узор оригами для любой трехмерной формы, наматывая длинную полоску бумаги.На практике полученные формы были слабыми из-за ряда «швов», которые приводили к слабым местам во всех конструкциях.
Спустя почти 20 лет профессор Демейн вместе с коллегой-экспертом по вычислительному оригами, профессором Томохиро Тачи из Токийского университета, должны раскрыть новый универсальный алгоритм, который генерирует узоры оригами с минимальным количеством швов.
«В 1999 году мы доказали, что можно сложить любой многогранник, но способ, которым мы показали, как это сделать, был очень неэффективным», — сказал профессор Демейн.
Программное обеспечение для компьютерной графики моделирует трехмерные фигуры — например, пляжный мяч — в виде многогранников с множеством крошечных треугольных сторон. Новый алгоритм создает узор, отображая эти плоские грани на плоской поверхности. Затем эту поверхность можно смять и собрать в желаемую форму.
«Предполагается, что новый алгоритм даст вам гораздо более удобные и практичные складки», — сказал профессор Демейн. «Мы не знаем, как это точно выразить математически, но на практике это работает намного лучше.”
«Но у нас есть одно математическое свойство, которое хорошо различает два метода […], которые мы называем водонепроницаемостью».
Создание выкройки с минимальным количеством швов означает, что «границы» исходной бумаги сохраняются. Более ранний алгоритм, который оборачивает вокруг себя тонкую полоску бумаги, менее водонепроницаем и менее эффективен. Например, создание кружки путем обертывания тонких полосок бумаги приведет к появлению множества крошечных границ, которые могут протекать, тогда как создание кружки из одного большого круга бумаги приведет к структуре только с одним зазором: отверстием в верхней части кружки. .
Этот алгоритм может использоваться в производстве для создания сложных объектов, например, из плоских листов пластика.
Исследователи работают над реализацией алгоритма в новой версии Origamizer, программного обеспечения для создания шаблонов оригами, разработанного профессором Тачи. Они представят свой новый алгоритм на симпозиуме по вычислительной геометрии в июле.
Подпишитесь на электронную рассылку новостей E&T, чтобы получать такие замечательные истории каждый день на свой почтовый ящик.
Математическое оригами — Написание антологии
Математическое оригами
Леланд Шиппер ’12
Старший математический семинар
Я нашел статью «Математическое оригами», написанную Леландом Шиппером, чрезвычайно интересной и очень хорошо написанной. Вдобавок, в отличие от многих математических сочинений, эта тема, казалось, была привлекательной для широкой аудитории. Она выделялась как одна из лучших газет для взрослых, которые я когда-либо читал.
— Том Линтон
Японское искусство оригами — это не только весело и круто, но и математически мощно. Используя только простые аксиомы оригами, немного творчества и времени, мы можем складывать поистине удивительные формы. Возможные применения этих форм оригами только начинают изучаться. Оригами используется для создания всего: от массивных космических телескопов до крошечных сердечных сокращений, используемых в хирургии после сердечного приступа. Границы оригами расширяются и проверяются каждый день.Связь между математикой и оригами существует на протяжении веков, но исследование этой связи и использование оригами для обучения математике как низшего, так и высшего уровня быстро растет. И хотя оригами все чаще используется для обучения математике, математика также используется для доказательства большого количества теорем об оригами. Например, в этой статье мы покажем, как математика может помочь нам выполнить плоскую вершинную складку квадрата, используя интересный метод скручивания.Применение математики к складыванию бумаги позволяет нам сузить круг вопросов, сколько и какой тип складок мы должны использовать для правильного создания плоских моделей складывания. В то же время математика может использоваться и для обратного; это помогает нам исследовать, сколько разных складок мы можем сделать — и насколько далеко зашли границы оригами.
Прежде чем мы исследуем метод скручивания для выполнения плоского сгиба вершины на квадрате, нам нужно немного поближе познакомиться с оригами, его руководящими принципами и некоторыми ключевыми определениями.Во-первых, давайте начнем с определения оригами.
Оригами: японское искусство складывания из бумаги декоративных фигур и фигур.
Важно понимать, что это очень широкое определение оригами. В оставшейся части статьи мы будем использовать гораздо более ограниченный взгляд на Оригами; Мы будем придерживаться семи аксиом. Первые шесть были представлены Хумьяки Хузитой в 1991 году и называются Аксиомами Хузиты, а седьмая аксиома была написана Коширо Хатори в 2001 году.Эти семь аксиом обычно считаются чистейшей формой оригами, и мы будем использовать их, чтобы управлять способами складывания бумаги для создания форм оригами. Семь аксиом таковы:
1. С учетом двух точек p1 и p2 существует уникальная складка, которая проходит через обе из них.
2. С учетом двух точек p1 и p2 существует единственная складка, которая помещает p1 на p2.
3.Для двух прямых l1 и l2 есть складка, которая помещает l1 на l2.
4. Для точки p1 и прямой l1 существует единственная складка, перпендикулярная l1, которая проходит через точку p1.
5. Для двух точек p1 и p2 и прямой l1 имеется складка, которая помещает p1 на l1 и проходит через p2.
6. С учетом двух точек p1 и p2 и двух прямых l1 и l2 получается складка, которая помещает p1 на l1 и p2 на l2.
7. Для одной точки p и двух прямых l1 и l2 получается складка, которая помещает p на l1 и перпендикулярна l2.
Учитывая эти семь аксиом, мы можем создать миллионы форм оригами, но использование только этих аксиом действительно ограничивает нас в некотором смысле. Например, эти аксиомы не позволяют нам использовать такие техники, как мокрое оригами, которое позволяет нам создавать изогнутые линии, созданные путем смачивания бумаги и формования бумаги, для создания форм, которые невозможно создать с использованием чистых техник оригами. Он запрещает использование модульного оригами, которое позволяет комбинировать и объединять разные листы бумаги в одну форму оригами.И, наконец, это мешает нам разрезать бумагу любым способом, который разрешен в ветке оригами под названием Киригами.
Есть несколько способов отобразить выкройки оригами, самый подробный из которых называется схемой оригами. Если вы ищете оригами в Интернете и распечатываете выкройку, вы обычно будете смотреть на схему оригами. Эти диаграммы не только показывают, где вам нужно сбросить карты, но и используют пронумерованные шаги для определения последовательности ходов. Хотя эти шаблоны полезны для папок новичков, их слишком сложно создавать и использовать, поскольку оригами становится все сложнее.По этой причине большинство художников оригами, которые используют математику для создания своих творений, используют так называемый шаблон складок оригами. Эти шаблоны обычно дают вам только две части информации: где возникают складки и какой это тип складки. В шаблоне сгиба нет последовательности, и автор может решить дополнительно ограничить информацию, предоставляемую шаблоном сгиба, нарисовав все линии одинаково, чтобы пользователь сам определил, какой тип сгиба необходим. Ниже приведен пример шаблона складки и полученного в результате создания оригами.
Как вы понимаете, это довольно сложный узор сгиба, для которого практически невозможно создать точную последовательность. Чтобы правильно сложить этот узор складок, вы должны иметь базовое понимание оригами и некоторых техник складывания. Один из ключей к пониманию рисунка складок — это способность различать гору и долину. Горный сгиб — это складка, которая вогнута вниз, так что бумага сгибается от вас, в результате чего сгиб оказывается ближе всего к вам.Сгиб в форме долины — это обратная сторона: складка, которая вогнута вверх, так что бумага сгибается к вам, в результате чего складка находится дальше всего от вас. Обе складки показаны ниже.
Авторы складок используют разные линии, чтобы различать горы и долины; с этого момента в наших рисунках складок мы будем различать горы и долины, используя тонкие или пунктирные линии для долин и жирные линии для гор.
Одна из областей оригами, которая в последнее время изучается с большим интересом, — это концепция складывания в плоскости.Складываемость относится к способности складывать узор сгиба модели оригами так, чтобы она лежала полностью ровно, используя только наши чистые техники оригами. Поскольку математика применялась к оригами в последние два десятилетия, мы многому научились в области складываемых плоских фигур. В оставшейся части этой статьи мы исследуем возможные шаблоны складок для выполнения плоского складывания квадратного перекрученного образца складки, что повлечет за собой плоское складывание в четырех вершинах, но пока давайте просто проанализируем одну плоскую складку вершины, чтобы получить представление о том, как это работает.Если вы посмотрите на рисунок 1 ниже, мы сможем увидеть некоторые интересные свойства складывания в плоскую форму. Например, для каждой складки в круговой складке мы можем назначить ее горной складкой или долиной. Следовательно, у нас есть простая задача комбинаторики, которая расскажет нам, сколькими различными способами мы можем сложить этот узор складки. Чтобы решить эту проблему, мы применяем фундаментальный принцип подсчета, который гласит: если есть m способов выполнить одну задачу и n способов выполнить другую, то есть mn способов выполнить обе задачи.Следовательно, поскольку в сгибе ниже у нас есть четыре складки, чтобы назначить складки горы или долины, у нас есть 24 = 16 возможных моделей оригами, которые мы можем создать из этого узора сгиба с одной вершиной. Важно отметить, что большинство этих выкроек на самом деле не складываются. Например, если у вас есть все складки гор или все складки долин, невозможно сложить модель, не сгибая ее в местах, не указанных в шаблоне складок.
Изучение свойств, определяющих складываемость при плоской складке, является задачей, которая в последнее время активно изучается.Следующие четыре свойства должны выполняться, чтобы данный шаблон сгиба с одной вершиной был плоским.
1. Шаблон сгиба должен быть двухкратным. Это похоже на концепцию проблемы четырехцветной карты, но вместо использования четырех цветов мы можем использовать только два, чтобы убедиться, что никакие два соприкасающихся участка нашего шаблона складки не имеют одинаковый цвет. Ниже приведен пример двухцветного рисунка складки.
2. Теорема Кавасаки: Теорема Кавасаки: дана вершина в плоском шаблоне складок оригами, обозначьте углы между складками как α1, α2,…, α2n по порядку.Тогда должно быть: α1 + α3 +… + α2n-1 = α2 + α4 +… + α2n = 180 °. Применяя теорему Кавасаки еще раз к рисунку 1 на предыдущей странице, мы можем заключить, что для того, чтобы модель была плоско складываемой, α1 + α3 = 180 ° и α2 + α4 = 180 °.
3. Теорема Маэкавы: дана вершина в плоском образце складок оригами, если M — количество горных складок, а V — количество складок долин в вершине, тогда мы должны иметь M-V = ± 2. Например, если мы вернемся к рисунку 1 на предыдущей странице, мы увидим, как теорема Маэкавы может быть применена к шаблону складок.Поскольку у нас четыре складки, у нас не может быть всех гор или всех долин, иначе мы нарушим теорему Маэкавы, потому что количество складок гор и долин будет отличаться на четыре. Мы также нарушаем теорему, если у нас есть по две складки каждого типа. Таким образом, у нас есть только один правильный выбор: либо три складки гор и одна складка долины, либо три складки долины и одна горная складка.
4. Лист никогда не должен проникать в складку. На самом деле, с бумагой лист никогда не может проникнуть через складку; вместо этого вам придется разрезать или порвать бумагу или создать складки, не указанные в шаблоне складки.По сути, это правило, которое не дает нам «жульничать», когда мы складываем наши модели оригами. Это свойство на самом деле довольно интуитивно понятно и является наименее техническим из всех свойств, но его сложнее всего реализовать. Первые три свойства можно легко запрограммировать и использовать для решения проблем сгибаемости с помощью компьютера. Это последнее правило, из-за которого разработка алгоритма оказалась чрезвычайно сложной. В этой области был достигнут некоторый прогресс, и в течение последнего десятилетия компьютерные ученые кооптировались с математиками, чтобы доказать, что определение складок гор и долин в образе складок таким образом, чтобы лист никогда не проникал сквозь складки, эквивалентно логической задаче: вычислительно NP-полный.NP-полные логические задачи могут легко потребовать полного курса для понимания алгоритмов и программирования, необходимых для их решения, но важно то, что лидеры в области оригами нашли способы использовать компьютеры для решения проблем плоской складываемости, которые человеческий разум никогда не мог полностью обработать. Одним из программируемых алгоритмов, которые являются ключевым элементом в решении этих проблем, является теорема о большом-маленьком-большом угле, которая гласит: в плоской вершинной складке, если у нас есть последовательность последовательных углов αi-1, αi и αi + 1 с αi-1> αi и αi <αi + 1, то две линии перегиба между этими тремя углами не могут иметь одинаковую четность горной долины.Это будет единственная теорема, которая нам понадобится позже в этой статье для нашего основного результата, но есть еще несколько теорем и алгоритмов, которые помогают нам придерживаться этого четвертого правила для всех шаблонов складок оригами.
Теперь, когда мы понимаем элементы, необходимые для демонстрации того, что шаблон складки с одной вершиной можно складывать плоско, давайте рассмотрим шаблон складки, который, несомненно, является более сложным и может применяться как в художественной, так и в практической сферах оригами. Этот узор складок называется квадратным скручиванием, потому что при складывании бумага «скручивается» в меньший квадрат; его складка дана ниже без привязки к горам и долинам.
Эта модель оригами не только имеет множество применений, которые мы обсудим позже, но она также является отличной моделью для обсуждения некоторых математических аспектов, которые мы можем использовать для исследования плоской складываемости моделей складок и в более широком смысле для изучения пределы оригами. Первое, что вы должны заметить в этом шаблоне складки, это то, что сложить его ровно будет намного сложнее, чем сложить шаблон складки с одной вершиной. У этого шаблона четыре вершины, и в каждой вершине мы должны соблюдать четыре основных правила плоской складываемости.По своей конструкции рисунок сгиба уже соответствует первым двум правилам плоской складываемости. Он двухцветный и соответствует теореме Кавасаки. Поскольку наш рисунок складок по своей природе соответствует нашим первым двум правилам, наша цель — использовать последние два правила, а именно теорему Маэкавы и теорему о большом-маленьком-большом угле, чтобы доказать, сколько различных назначений гор и долин возможно, в то время как по-прежнему оставаясь верным нашим аксиомам оригами и нашим четырем свойствам плоской складываемости.
Во-первых, давайте рассмотрим самое основное назначение складок гор и долин для этого рисунка складок, чтобы лучше понять, что мы пытаемся сделать.Первый рисунок на следующей странице — это узор изгибов с горами, обозначенными жирными линиями, а долины — тонкими линиями. Второй рисунок — это изображение модели оригами после того, как мы сложим по схеме складки.
Чтобы лучше понять, чего мы пытаемся достичь, давайте начнем рассматривать, сколькими способами мы можем назначить складки гор и долин шаблону складок квадратного скручивания. Если мы изучим приведенный выше образец сгиба, мы обнаружим, что на нем обозначено двенадцать линий сгиба.Следовательно, если мы применим фундаментальный принцип подсчета, учитывая, что у нас есть двенадцать линий сгиба, чтобы назначить складку горы или складку долины, существует 212 или 4096 возможных назначений гор и долин. К счастью, это количество намного больше, чем количество уникальных плоских складных моделей. Это завышение оценок по двум причинам; Во-первых, это число учитывает все задания в горах и долинах, которые у вас могут быть, но многие из них нарушают наши третье и четвертое основные правила. Например, одно из назначений из 4096 возможных — это узор складок со всеми складками гор, но это не поддерживает теорему Мавекавы, потому что количество складок гор и долин будет отличаться на 12 вместо 2.Вторая причина, по которой 212 является завышенной оценкой, заключается в том, что существует большое количество решений, которые не являются уникальными, а вместо этого представляют собой простой поворот на 90 °, 180 ° или 270 ° другого решения. Позже мы увидим несколько таких примеров. Следовательно, чтобы найти количество уникальных плоских складных решений, нам нужно будет найти способ отсеять все эти повторы и не плоские складные модели.
Во-первых, давайте устраним все решения, которые не поддерживают теорему Маэкавы и / или теорему о большом-маленьком-большом угле и, следовательно, не являются плоскими складываемыми.Один из способов сделать это — посмотреть на все 4096 шаблонов складок и проанализировать их по отдельности, чтобы найти, какие из них не соответствуют нашим основным правилам. Однако доказывать это истощением было бы утомительно. Вместо этого, если мы изучим наш образец складки квадратного скручивания, мы можем сделать вывод, что если мы выберем назначение горы и долины для двух складок в каждой вершине, то мы сможем применить теорему о большом-маленьком-большом угле, чтобы сказать нам, какое назначение для сделайте третью складку в каждой вершине. Затем, когда у нас есть три сгиба в каждой вершине, теорема Маэкавы диктует назначение четвертой и последней складки в каждой вершине.Поэтому все, что нам действительно нужно сделать, это назначить складки гор и долин двум складкам в каждой вершине. Самый простой способ назначить две складки в каждой вершине — это назначить четыре центральных складки, которые составляют ромбовидную форму внутри шаблона складок. Если мы выберем горы и долину для этих четырех складок ромба, мы назначим по две складки в каждой вершине, и, таким образом, остальные складки в узоре будут систематически назначаться с использованием наших последних двух основных правил.Диаграммы на следующих двух страницах помогут нам изучить, как происходит это систематическое присвоение, когда мы применяем теорему Маэкавы и теорему о большом-маленьком-большом угле.
Давайте сначала предположим, что весь наш узор складок представляет собой складки долин (обозначенных здесь пунктирными линиями), и мы собираемся изменить некоторые из них на складки гор, где это уместно. Затем давайте произвольно назначим внутреннему алмазу складки гор и долин. В приведенном ниже примере я назначил две горные складки, так что складки j и m являются горами, а n и q остаются долинами.Это лишь один из многих примеров, которые мы могли бы оценить.
Давайте сначала рассмотрим вершину B, и мы увидим, как мы можем использовать наши последние два основных правила. В вершине B (и в каждой вершине) мы можем применить теорему об углах Big-Little-Big. Условия теоремы выполняются, потому что угол, содержащийся в складках j и k, меньше обоих углов, окружающих его. Таким образом, мы можем использовать эту теорему, чтобы установить, что складки j и k не могут иметь одинаковое соотношение гора / долина.Поскольку мы уже назначили j складкой горы, это означает, что k должна оставаться складкой долины, как уже указывалось. Итак, теперь в вершине B нам назначены три складки: j и m — горы, а k — долина. Теперь мы можем применить теорему Маэкавы, чтобы определить присвоение складки l. Поскольку, если мы оставим l как долину, как указано в настоящее время, количество складок гор и долин будет отличаться на ноль, мы должны назначить l горной складкой, так что у нас будет три горы и одна долина, а значит, разница будет равна двум.Таким образом, в вершине B мы имеем следующие складки, которые делают ее плоской складной в вершине B.
Теперь мы можем применить ту же логику к вершине C, используя теорему об углах Big-Little-Big для определения складки горной складки. Затем, чтобы поддержать теорему Маэкавы, мы должны также отнести складку p к складке горы. Таким образом, модель теперь плоско складывается в вершинах B и C. Если мы продолжим делать это в каждой вершине, мы получим следующий шаблон плоской складки. Мы могли бы применить эти две теоремы, чтобы систематически назначать горы и долины для восьми внешних складок, независимо от того, что мы выбрали для нашего внутреннего алмаза.
Мы могли бы выбрать назначение от нуля до четырех гор во внутреннем ромбе, и мы могли бы разместить эти назначения где угодно, и тогда мы могли бы использовать наши две теоремы таким же образом, как показано выше.
Теперь, когда мы понимаем, что после того, как мы выбрали назначение горы и долины для внутреннего ромба, последние два фундаментальных правила систематически относят все складки к горам или долинам, мы можем отбросить большинство из 4096 возможных назначений.Поскольку на внутреннем ромбике всего четыре складки, для которых мы выбираем назначение горы и долины, существует только 24 или 16 возможных плоских складных решений. Но помните, что есть еще значительная часть этих решений, которые не являются уникальными решениями, а напротив, симметричны друг другу по оси вращения. Например, когда мы назначаем одну горную складку внутреннему алмазу, мы можем назначить ее четырем разным местоположениям. Эти четыре возможности показаны ниже.
Если вы присмотритесь, то заметите, что эти четыре решения представляют собой просто вращения друг друга.Если бы перед вами были эти четыре шаблона складок, все они были бы одинаковыми; это будет просто вопрос того, как вы на это смотрите. Таким образом, в интерьере ромба есть только одно уникальное решение с одним горным назначением. Подобным образом есть четыре полных решения с тремя назначениями гор в внутреннем ромбе, но только одно из них является уникальным. Однако есть два разных уникальных способа сопоставить две горные складки в алмазе. Мы можем назначить их рядом или напротив друг друга.И, наконец, есть только один способ назначить все горы или ни одного из них во внутреннем ромбе. Следовательно, после отбрасывания всех осесимметричных решений остается только шесть уникальных способов назначить горы и впадины шаблону складок, чтобы получить плоский складываемый квадратный поворот. Они показаны ниже, начиная с четырех гор, назначенных на внутреннем алмазе, затем трех, затем двух способов назначить две, затем одной и, наконец, без гор, назначенных на алмазе.Эта модель может показаться несколько тривиальной, но квадратный поворот находит решение фундаментального вопроса в мире оригами: как нам взять большой объект, сложить его в что-то меньшее и сделать это таким образом, чтобы на это ушло минимум усилий. количество сил, воздействующих на него, чтобы вернуть его к исходному размеру. Квадратная скрутка, однажды сложенная вниз, требует всего двух сил (тяги от любых двух углов), чтобы расширить ее до нормального размера. С другой стороны, если бы мы просто сложили бумагу любым способом, которым мы хотели бы уменьшить ее, вероятно, потребовалось бы несколько сил, чтобы развернуть ее до исходного размера.Квадратное скручивание также называется складкой тесселяции, что означает, что его можно повторять несколько раз, чтобы мы могли взять произвольный большой узор сгиба, и мы можем сложить его до модели, которая будет такой же маленькой, как и материал, который мы складываем с желанием. позвольте нам продолжить делать складки.
Реальное применение таких складок просто потрясающе. Например, многоугольный поворот, очень похожий на квадратный поворот, который мы только что рассмотрели, используется доктором Робертом Лангом, чтобы отправить телескоп диаметром 100 метров в космос.Поскольку в ракете нет места для телескопа такого размера, доктор Ланг помогает НАСА использовать оригами, чтобы сложить большую линзу таким образом, чтобы она могла поместиться в ракету на Земле, а затем легко расширяться в космосе. .
Origami доказала свою эффективность в приложениях, которые ежедневно спасают человеческие жизни, таких как сердечные стенты и подушки безопасности. Сердечные стенты используются для удержания артерий открытыми у пациентов, перенесших сердечный приступ, и они складываются в очень маленькие капсулы, чтобы их можно было протянуть через артерию и расширить, когда она достигнет места назначения.Автомобильные подушки безопасности также необходимо аккуратно сложить, чтобы они поместились в очень маленькое пространство, но они должны быть сложены таким образом, чтобы они могли расширяться за считанные миллисекунды. Без использования оригами расширение подушки безопасности могло бы занять гораздо больше времени, потому что для правильного расширения подушки необходимо было бы воздействовать на нее несколькими силами.
В оригами удивительно то, что по сравнению с другими областями прикладной математики оно все еще находится в примитивном возрасте. Мы только начинаем раскрывать весь потенциал оригами.Новые теоремы открываются и используются программистами в области компьютерных наук каждый день, чтобы продолжать продвигать эту область дальше, чем кто-либо мог себе представить. Его уже используют для создания прекрасных произведений искусства, чтобы заглянуть в космос дальше, чем мы когда-либо видели, и для спасения бесчисленных жизней, но кто знает, куда он приведет нас в будущем, поскольку мы продолжаем использовать математику для исследования его границ.
цитируемых работ
Халл, Томас. Проект оригами: упражнения для изучения математики.Уэлсли, Массачусетс: A K Peters, Ltd, 2006.
Халл, Томас. «Комбинаторика плоских складок: обзор». Труды Третьей Международной встречи оригами: наука, математика и образование. А. К. Петерс; 2002.
Ланг, Роберт. Роберт Дж. Лэнг Оригами. 2011. Интернет. 14 ноября 2011 г.
Шаблоны для вырезания / фальцовки для бумажных механизмов
нет. 01
Flexagon
Повторяющаяся четырехкадровая прямоугольная анимационная конструкция
Сгибание карты в соответствии с ее материальной памятью переносит получателя через историю из 4 кадров.Подробнее здесь.
Ваш браузер не поддерживает видео тег.
нет. 02
Hexaflexagon
4 повторяющихся кадра
Гексафлексагон — это бумажная игрушка, рекламное устройство отображения, «приспособление для повествования» и интерактивная демонстрация геометрии, требующая физической активации для «чтения». Благодаря действиям изгиба, скручивания или вращения эти бумажные гаджеты открывают последовательные, зацикленные кадры, обеспечивая захватывающий формат для рассказа историй и анекдотов, для раскрытия вложенной информации, для создания произведений искусства или просто для того, чтобы обеспечить удовлетворительную отдушину для нервничающих. энергия.Более подробная информация здесь, в статье для журнала How Magazine .
Ваш браузер не поддерживает видео тег.
нет. 03
5-сторонняя складная трубка
Ауксетический метаматериал
Источник: предоставлено Эраной Кратунис во время выступления Code-Paper-Scissors в SFPC.
нет. 04
Пружинное поведение
Ауксетический метаматериал
Источник: Йоханнес Овервельде, Джеймс Уивер, Чак Хоберман и Катя Бертольди, Рациональный дизайн реконфигурируемых призматических архитектурных материалов, Nature 541, 347-352, 19 января 2017 г.
Ваш браузер не поддерживает видео тег.
нет. 05
Miura-ori Fold
«Программируется» путем деформации частей шаблона
Попробуйте изменить углы
Фальцовка Miura (ミ ウ ラ 折 Miura-ori) — это метод складывания плоской поверхности, например листа бумаги, на меньшую площадь. Складка названа в честь ее изобретателя, японского астрофизика Корио Миура. [1] Образцы складок Miura образуют мозаику поверхности параллелограммами.В одном направлении складки лежат вдоль прямых линий, причем каждый параллелограмм формирует зеркальное отражение своего соседа через каждую складку. В другом направлении складки зигзагообразны, и каждый параллелограмм является перемещением своего соседа по складке. Каждый из зигзагообразных путей складок состоит исключительно из горных складок или изгибов долин, причем горы чередуются с долинами от одного зигзагообразного пути к другому. Каждый из прямых участков складок чередуется между горными и долинными складками.[2] Сгиб Миура — это форма жесткого оригами, что означает, что складывание можно выполнять непрерывным движением, при котором на каждом шаге каждый параллелограмм является полностью плоским. Это свойство позволяет использовать его для складывания поверхностей из жестких материалов. Например, большие массивы солнечных панелей для космических спутников в японской космической программе были сложены Miura перед запуском, а затем разложены в космосе. [3] [4] Сложенная складка Miura может быть упакована в компактную форму, ее толщина отражает только толщину сложенного материала.Сложенный материал можно распаковать одним движением, потянув за противоположные концы, и аналогичным образом сложить, сдвинув два конца вместе. В применении к солнечной батарее это свойство уменьшает количество двигателей, необходимых для раскрытия этой формы, уменьшая вес и сложность. (Википедия)
Ваш браузер не поддерживает видео тег.
нет. 06
Бистабильный механизм
Попробуйте различные размеры, чтобы отрегулировать силу бистабильного «щелчка»
Источник: Группа Итаи Коэна, Корнельский университет. Это единичный элемент квадратного скрученного узора.С математической точки зрения, этот шаблон складывания можно раскладывать. В результате получается бистабильный механизм — своего рода бумажный переключатель.
Ваш браузер не поддерживает видео тег.
нет. 07
Шестиугольный мигалка для оригами
Мигалки — это разборные складные конструкции. Этот дизайн был разработан Джереми Шафер. Подробнее о математике работы флешеров здесь.
Ваш браузер не поддерживает видео тег.
нет. 08
Поворотный кулачок с рычагом
Эта структура демонстрирует, как идеи машиностроения могут быть адаптированы к бумажной инженерии. Пользователь поворачивает колесо, чтобы задействовать продолговатый кулачок. Из-за неодинаковой геометрии кулачка установленный рычаг оживляется преувеличенно и неожиданно. Адаптировано из книги Дэвида Картера The Elements of Pop-up.
Ваш браузер не поддерживает видео тег.
нет. 09
Двойное слепое обнаружение
Растворение
Эта форма упрощает традиционную структуру жалюзи до простой двухслойной конструкции. Адаптировано из книги Дэвида Картера The Elements of Pop-up.
Ваш браузер не поддерживает видео тег.
нет. 10
Линейно-вращательное движение
Эта конструкция с язычком может приводиться в движение вручную или при открытии и закрытии книги.Он прочный и обеспечивает вращательное движение до 80 градусов. Адаптировано из книги Дэвида Картера The Elements of Pop-up.
Ваш браузер не поддерживает видео тег.
нет. 11
Ударный объект
Шумогенератор
Зазубренные кромки, проходящие через заслонки, производят ударную силу разной скорости. Он прочный и обеспечивает вращательное движение до 80 градусов. Адаптировано из книги Дэвида Картера The Elements of Pop-up.
нет. 12
Модифицированная водная бомба
Классический узор из складок «водяная бомба», разделенный пополам, — один из наиболее часто используемых базовых узоров в оригами. Геометрия подъема и опускания (а также сжатия и расширения) водяной бомбы исследуется в качестве альтернативного метода настройки различных типов антенн. В этих тестах бумага напечатана с дипольными и квадратными проводящими элементами и, по мере движения бумаги, используется для настройки антенн, датчиков и отражателей.Этот шаблон сгиба оказался эффективной структурой, предлагая способ чувствительного управления резонансной настройкой таких компонентов. Эта модифицированная версия переворачивает все остальные ромбы.
нет. 13
Последовательные выкройки складывания
Шаблоны складывания, которые производят очень разные типы (и направления) движения, могут быть последовательно объединены на одном листе. Такое комбинирование паттернов дает возможность вложить вторичные функции в функцию первичного паттерна.В этом примере шарнирное действие миура-ори поднимает и опускает ряд кубиков. В свою очередь, неразборные кубики действуют как прокладка, останавливая путь складки миура-ори до полностью свернутого состояния. Ширина куба определяет как время, так и расстояние этого интервала.
Ваш браузер не поддерживает видео тег.
нет. 14
Квадратная скрутка
Образец складывания квадратной закрутки состоит из пересечения двух перпендикулярных складок.При развертывании (потянув влево / вправо или вверх / вниз) структура расширяется во всех направлениях, поскольку складки поднимаются и вращают свои квадратные вершины. Модульная единица, составляющая эту мозаику, представляет собой квадратный бумажный «переключатель» — бистабильную структуру, которая открывается или закрывается. Квадратную скрутку сложить очень сложно. Открытие и развитие этого рисунка было запечатлено в книге Рона Реша «Paper and Stick Film».
Ваш браузер не поддерживает видео тег.
нет.15
Поворотное раскрытие на 360 °
Растворение
Этот документ показывает структуру, функционирующую так же, как створчатый затвор в объективе камеры, и перемещается между двумя разными изображениями. Шаблон изменен на основе оригинального источника: Изготовление механических карточек: 25 дизайнов из бумаги Шейлы Старрок
Ваш браузер не поддерживает видео тег.
нет. 16
Противоположные петли
Активируется при открытии и закрытии карты.Эта форма, вероятно, возникла у учеников Йозефа Альбера в Баухаусе.
Ваш браузер не поддерживает видео тег.
нет. 17
Роторельеф бумага
Инертный в неподвижном состоянии, иллюзия при вращении, эта двухслойная конструкция Tor Lokvig, управляемая язычками, напоминает роторельефы Дюшана .
Ваш браузер не поддерживает видео тег.
нет.18
Разнонаправленный шарнир Illusion
Эта форма, вероятно, возникла у учеников Йозефа Альбера в Баухаусе.
Ваш браузер не поддерживает видео тег.
нет. 19
Flasher
Анимированная, сворачивающаяся, ауксетическая структура
В 2012 году эта конструкция вспышки была использована Лабораторией совместимых механизмов в Университете Бригама Янга (которая разрабатывает механизмы, вдохновленные оригами) для разработки спутника на солнечных батареях для JPL-NASA.Симуляция его вращения вокруг Земли может быть показана в документальном фильме The Origami Revolution. Смотрите здесь. Лаборатория реактивного движения использует ту же конструкцию, чтобы блокировать свет, падающий от звезд, из находящегося там источника: «Команда BYU / JPL-NASA выдвинула это как концепцию, но она еще не доработана, чтобы летать в космосе. Мы» Но мы работаем над этим! » Самый последний прототип здесь.
Ваш браузер не поддерживает видео тег.
нет.20
Форма бесконечности
Оптическая иллюзия
Мы полагаем, что эта форма возникла у учеников Йозефа Альбера в Баухаусе.
нет. 21
Форма 360 °
Оптическая иллюзия
Мы полагаем, что эта форма возникла у учеников Йозефа Альбера в Баухаусе.
нет. 22
Rotary Hidden Picture Reveal
Эта структура часто встречается на викторианских поздравительных открытках.Шаблон изменен на основе оригинального источника: Изготовление механических карточек: 25 дизайнов из бумаги Шейлы Старрок
Ваш браузер не поддерживает видео тег.
нет. 23
Игрушка плиссе Troublewit
Эта трансформирующаяся структура, меняющая форму, была популяризирована в бумажных перформансах, называемых «Troublewit» (которые часто появлялись как небольшой сегмент в большом волшебном шоу). Шаблон был адаптирован из «Техники складывания для дизайнеров » Пола Джексона.
Ваш браузер не поддерживает видео тег.
нет. 24
Диагональная венецианская шторка Reveal
Эффект растворения
В этой конструкции используются четыре «жалюзи», чтобы открыть скрытое изображение с помощью язычка. Шаблон изменен на основе оригинального источника: Изготовление механических карточек: 25 дизайнов из бумаги Шейлы Старрок
Ваш браузер не поддерживает видео тег.
нет.25
Квадратные сильфоны-гармошки
Единственная форма, которая одновременно светонепроницаема и складывается! В камерах первого обзора использовались сильфоны, позволяющие оператору регулировать фокусное расстояние. Шаблон изменен на основе dielines для Эта книга — камера , созданная Келли Андерсон.
нет. 26
Бумажная сетка
Эффект растворения
Эта структура часто встречается на викторианских поздравительных открытках и требует веревки, чтобы приподнять «сетку» бумаги, чтобы открыть фотографию внизу.Шаблон изменен на основе оригинального источника: Изготовление механических карточек: 25 дизайнов из бумаги Шейлы Старрок
нет. 27
Традиционные жалюзи
Dissolve Effect
Когда пользователь тянет за язычок, четыре жалюзи отодвигаются, открывая скрытое изображение. Считается, что этот формат возник у Лотара Меггендорфера. Шаблон адаптирован из первоисточника: Изготовление механических карточек: 25 дизайнов из бумаги Шейлы Старрок
Ваш браузер не поддерживает видео тег.
нет. 28
Форма 90 °
Оптическая иллюзия
Мы полагаем, что эта форма возникла у учеников Йозефа Альбера в Баухаусе.
нет. 29
Форма 90 °
Оптическая иллюзия
Мы полагаем, что эта форма возникла у учеников Йозефа Альбера в Баухаусе.
нет. 30
Форма 180 °
Формовочная
Мы полагаем, что эта форма возникла у учеников Йозефа Альбера в Баухаусе.
нет. 31
Отдельностоящая форма
Это гексафлексагон, приклеенный на подставку, который показывает олоидную траекторию его инверсии.
Подробнее о сборке гексафлексагона здесь — в статье для журнала How Magazine
Ваш браузер не поддерживает видео тег.
нет. 32
Раздвижная карточка
Эффект вытягивания и вращения
нет.33
Наклонный язычок
Потяните язычок, чтобы изменить угол наклона
Ваш браузер не поддерживает видео тег.
нет. 34
Всплывающая подставка-гармошка
Подставка-гармошка, которая открывается и всплывает при открытии книги.
Ваш браузер не поддерживает видео тег.
оригами в форме звезды из бумаги Сложите правый нижний край поверх левой еще раз.Сложите левую сторону верхнего сгиба так, чтобы левый край и верхний край совпали. Имеет цветок спереди и квадрат сзади звезды. 01 апреля 2020 г. · Крисси Пушкин, также известная как Крисси Пк, является экспертом в области оригами и поделок из бумаги и писателем с 15-летним опытом. Хороший начальный размер — около 30 см или 1 фут в длину и около 1 см в ширину или около полдюйма. бумажные звезды оригами 2022 | Лучшее легкое изготовление бумажной звезды | Цветная бумага Star easy | @Cf origamiНаши новые каналы на YouTube: 1.12 октября 2018г. 2см. 6 из 5 звезд. Тщательно обрежьте внешние (черные) линии, чтобы удалить модель Starshade. Сверните бумагу и загните складки пятиугольника, так как оригами создает пятистороннюю геометрическую фигуру. gl / Iim0DkКак сделать бумажный ПОДАРОЧНЫЙ СУМК https: // www 540 листов Бумага для оригами в виде звезд, BENBO Двенадцать созвездий Украшение для рукоделия Космическое пространство Небо Оригами Lucky Star Paper Складные бумажные полосы оригами в виде звезд для художественных промыслов из бумаги. Бумажные звезды, кольца и венки.Сделайте оригами звезду из компаса. Этот предмет Бумага для оригами, Бумага с рисунком звезд в ассортименте цветов — 1005 листов, 2. Paperkiddo 800 листов Бумага для оригами со звездами 8 различных рисунков мраморного узора для поделок из бумаги Дети Взрослые Школьные учителя складывают бумажные полоски со звездами оригами. Также называется метательной звездой сюрикена. Эта надувная звезда оригами выглядит как гигантская счастливая звезда оригами. В качестве особого сюрприза поместите звезду оригами в коробку для завтрака. Набор из бумаги оригами также идеально подходит для различных случаев, таких как дни рождения, День матери, День отца, Хэллоуин, День святого Валентина в магазине Shenhai в магазине Amazon Arts, Crafts & Sewing.Чтобы упростить получение формы пятиугольника, я создал для вас два шаблона для печати. 71. Оберточная бумага — отличная альтернатива бумаге для оригами. Добавить в избранное. Узнайте, как сложить суперлегкую звезду оригами из двух квадратных листов бумаги. бумажные звезды оригами 2022 | Лучшее легкое изготовление бумажной звезды | Цветная бумага Star easy | @Cf origamiНаши новые каналы на YouTube: 24 ноября 2017 г. · Как сложить звезду оригами (второй стиль) 1. Изготовление оригами из бумажных звезд 2022 | Лучшее легкое изготовление бумажной звезды | Цветная бумага Star easy | @Cf origamiНаши новые каналы на YouTube: Как сделать звезду оригами-ниндзя: Привет, в этой инструкции я покажу, как сделать классную звезду оригами-ниндзя или сюрикен.Шаблон отформатирован для печати на бумаге размером 11 на 17 дюймов, что упростит складывание, но его также можно распечатать на бумаге меньшего размера. 24 ноября 2017 г. · Как сложить звезду оригами (второй стиль) 1. Учебное пособие по оригами «Компас-роза» — 8-конечная звезда. 24. Распечатайте. Переверните бумагу. Снова сложите пополам, чтобы отметить четверть пути. Бесплатная доставка подходящих товаров. 24 сентября 2021 г. · Коробка со звездой оригами — это традиционное японское оригами, в которое можно хранить небольшие подарки, монеты, скрепки, серьги и многое другое! Если вы уже немного разбираетесь в оригами, вам совсем не понадобится много времени, чтобы сделать эту маленькую шкатулку с сокровищами.Вы можете использовать любую бумагу, которая у вас есть под рукой, если она легкая (тонкая), а не картон. Когда полоска будет закончена, бумага должна стать «пухлой» и готовой к работе. Выполните те же действия, чтобы снова сложить обе половинки бумаги пополам, а затем сделайте треугольные сгибы на обоих концах обоих листов, которые станут точками звезды. Таким образом, из 12-дюймового квадрата получится 7-дюймовая звезда или 8,99 (AV Paper Series). 26 января 2021 г. · Инструкции по оригами в виде звезды: начните с квадратного листа бумаги для оригами и расположите его как ромб цветной стороной вверх.Лист бумаги размером 5 см x 1,5 дюйма x 11 дюймов и сложите его пополам. Красочная бумага оригами Lucky Star. Загните верхнюю точку вниз к нижней точке. 17 ноября 2015 г. · Мы любим оригами, потому что из клочков бумаги можно сделать почти все, в любое время и в любом месте! Это было бы отличным украшением для рукоделия 4 июля! Материалы Origami Star Wrath: 15 листов бумаги для оригами (США / Великобритания) (партнерские ссылки) (вы также можете использовать обычную бумагу для принтера или переработать несколько газет или журналов, разрезать их на квадраты 15×15 см) Оригами Star Эти звезды оригами несложны, но есть несколько шагов, которые сложно расшифровать с помощью одних только неподвижных изображений, поэтому я сделал видео о том, как делать звезды.VVVStudio. 3. Бумага для оригами, бумага с рисунком звезд в различных цветах — 1005 листов, 2. Сделайте из 1 листа квадратной бумаги. Для этой модели вам не понадобится большой лист бумаги: подойдет квадрат 10 х 10 см. Каждая звезда сделана из полоски бумаги размером примерно 10 на 1/4 или 1/2 дюйма. 50 или 100 оригами бумажных звездочек — Вырезанные вручную и сложенные вручную из блестящего металлического золота и белой бумаги — Счастливые бумажные звезды — Золотые звезды SGHandmade1 5 из 5 звезд (584) Симпатичные оригами Lucky Star бумажные полоски Складные звездные полоски.01 апр.2020 г. · Звезда на фото сделана из толстой золотой бумаги, аналогичную бумагу можно найти на Amazon или в ремесленных мастерских, однако вы можете использовать любую бумагу, которая вам нравится. Вырежьте это. 8 из 5 звезд. Крисси основала популярный веб-сайт и канал на YouTube Paper Kawaii, где она создает учебные пособия, шаблоны, бумагу для оригами для печати и поделки ручной работы. Любимый. Задняя часть звезды тоже очень красивая, а это значит, что ее тоже можно повесить в качестве украшения. 4 из 5 звезд. be / -PmgDnC_1l0Простая пятиконечная звезда из бумаги.75-дюймовая квадратная бумага для оригами Amazon Basics, разные цвета, 200 листов Toyo Thousand Paper Cranes Origami 7 см, 50 цветов, 1000 листов Убедитесь, что это подходит, введя номер вашей модели. Это лицевая сторона нашей бумаги для оригами, звезда оригами будет этого цвета. Пышная звезда оригами станет красивым украшением круглый год. 400 полосок белого цвета Оригами Lucky Stars среднего размера для складывания бумаги белого цвета. Эта поделка из бумаги подойдет любителям оригами и «Звездных войн» просто и весело. Звезды универсальны и могут использоваться практически на любой вечеринке или торжестве! Инструкции по изготовлению оригами звезд и венков находятся на двух страницах.Доступно только 3, и это в тележках для 4 человек. Разверните предыдущий шаг. Bonayuanda 1080 листов бумаги оригами звезды двусторонние складывающиеся полосы — 27 цветов. Вы можете распечатать шаблоны, вырезать их и обвести их на обратной стороне листа, который вы сложите в звезду. 2. 36. Загните нижний край к верхнему краю. Эта многослойная пятиконечная звезда оригами сделана из одного листа бумаги и сделать ее проще, чем вы думаете. Сложите верхние диагональные левый и правый края по диагонали, чтобы совместить с центральной складкой.На этот раз квадрат 5 дюймов, поскольку это была ширина бумаги, которую я использовал. Добавить к. Это не коробка, но ее можно повесить в качестве украшения или просто выставить на витрину, или сделать много и купить их в Shenhai в магазине Amazon Arts, Crafts & Sewing. 5 из 5 звезд. Я воспользовался приведенными здесь инструкциями, чтобы начать их создавать, но я подумал, что формат изображения всех шагов поможет другим (в основном из-за… 10 октября 2016 г. · 3D Paper Star Bowls — Материалы. Экономьте больше с помощью подписки и сохранения. 80. Сложите правую точку к левой.Эти бумажные звезды, кольца и венки — отличное развлечение во время рождественских праздников. 10 долларов. Разбросайте на столе много звезд оригами для патриотического или праздничного украшения. Подпишитесь на канал http: // ww 540 листов Бумага со звездами оригами, BENBO Украшение из двенадцати созвездий Ремесла своими руками Космическое небо Оригами Lucky Star Paper Складывание оригами Звездные бумажные полоски для художественных поделок из бумаги. Затем сгладьте края узла, чтобы он выглядел как пятиугольник, и загните короткий конец впадиной. Звезды универсальны и могут использоваться практически для всех торжеств! Щелкните здесь: Инструкции по изготовлению оригами звезд и венков находятся на двух страницах.5-дюймовый квадрат будет 5-дюймовой звездой. Звезды в этом уроке были сделаны из бумаги для вырезок, нарезанной на полоски размером 12 на 1/2 дюйма. БЕСПЛАТНАЯ ДОСТАВКА Оригами Сиба Ину Бумага для оригами Lucky Star Складная бумага для оригами с изображением собаки. 36. На каждом ходу вы будете покрывать разные части начальной базы. правый край бумаги. Это обратная сторона бумаги, обычно белая. Изготовление пятиконечной звезды оригами Этот предмет Бумага для оригами, бумага с рисунком звезд в различных цветах — 1005 листов, 2. Счастливую звезду оригами сделать так легко, но похоже, что скоро вы будете делать сотни! Вы делаете это из полоски бумаги.бумажные звезды оригами 2022 | Лучшее легкое изготовление бумажной звезды | Цветная бумага Star easy | @Cf origamiНаши новые каналы на YouTube: инструкции по созданию оригами Star Традиционная модель Origami Star — популярная и увлекательная модель; так что попробуйте использовать яркую бумагу: возможно, металлическая или даже блестящая бумага даст хороший эффект. 4 дюйма. Шаг первый Сделайте одну часть звезды. бумажные звезды оригами 2022 | Лучшее легкое изготовление бумажной звезды | Цветная бумага Star easy | @Cf origamiНаши новые каналы на YouTube: это лицевая сторона нашей бумаги для оригами, этого цвета будет звезда оригами.Делайте покупки Shenhai в магазине Amazon Arts, Crafts & Sewing. Загните правый край к левому краю. Возьмите 8. Прежде чем вы начнете складывать звезду, вам нужно вырезать из бумаги идеальный пятиугольник. бумажные звезды оригами 2022 | Лучшее легкое изготовление бумажной звезды | Цветная бумага Star easy | @Cf origamiНаши новые каналы на YouTube: 12 октября 2018 г. · Эти простые звезды оригами сложены из двух листов бумаги. 19 октября 2021 г. · Если вы хотите сложить звезду оригами, начните с того, что сложите и разрежьте пополам квадрат из бумаги для оригами или квадрат из бумаги, который вы сделаете сами.Использование шестидюймовой бумаги дает звезду 3. Как вырезать пятиконечную звезду. Чтобы придать форму звезды, воспользуйтесь линейкой. ; Бумага оригами звезда имеет 27 красивых цветов, каждый цвет около 50 листов, цвет: 27 конфетных цветов. Сложите бумагу пополам, чтобы получился прямоугольник. 50. Затем переверните пятиугольник и загните длинный конец полосы вдоль края пятиугольника. Вдавите конец в полоску бумаги. На странице 1 есть инструкции для звезд, сделанных из одного листа бумаги.352. Получите тонну цветной бумаги для принадлежностей для декоративно-прикладного искусства, проектов DIY, школьных презентаций, украшений и т. Д. Подпишитесь, чтобы получать больше потрясающих видео! https: // бит. При достаточной практике вы можете даже сделать их такими маленькими, как показано ниже. Раскройте. 5. Загните нижний правый угол поверх левого края. В этих звездах замечательно то, что единственный материал, который вам нужен, — это квадратная бумага, и я даже смог найти квадратную бумагу размером 12 x 12 дюймов в Michaels, так что мне не понадобилось 1. 13 июня 2018 г. · Сделайте квадратную бумагу. милая звезда оригами, созданная Масудом Хоссейни.Держите ножницы под рукой, так как они вам понадобятся в конце этих нескольких шагов. Как сделать крошечные звездочки оригами без ножниц: я люблю их делать, особенно на работе. 10 августа 2021 г. · Чтобы сделать звезду оригами, возьмите длинную полоску бумаги и завяжите узел на одном конце. 5 января 2018 г. · Узнайте, как сложить красивую шестиконечную звезду оригами, созданную Хосе Меусеном. С помощью иглы и нитки нанижите несколько звездочек в гирлянду. Если у вас возникли проблемы, сообщите мне в разделе комментариев.75-дюймовый квадрат. Или сделайте их пастелью в виде цветочков! 3D бумажные звездные чаши — инструкции. 27 октября 2021 г. · Можно также использовать бумагу для оригами. ly / 33SNrhK Моя бумага и размер: 2x бумага для принтера, A4 How To Make a Paper Ninja Star (Shuriken) — OrigamiWelco Посмотрите это видео здесь в простой для понимания версии https:// youtu. Эта геометрическая звезда оригами выглядит по-разному с каждой стороны. Внутренняя часть коробки будет этого цвета. Как сделать 3D звезду из бумаги | Легкие звездочки оригами для начинающих | Поделки из бумаги своими руками ПОДПИСАТЬСЯ: https: // goo.Я использовала восьмерку. Эти звезды, кольца и венки оригами очень весело делать во время рождественских праздников. 314. 75-дюймовая квадратная бумага для оригами Amazon Basics, разные цвета, 200 листов Toyo Thousand Paper Cranes Origami 7 см, 50 цветов, 1000 листов 25 мая 2020 г. · Если вы используете небольшую бумагу, например трехдюймовую, результат будет небольшим звездочка мерила только 1. Из магазина VVVStudio. 7 долларов. (7390) 2 доллара. Загните правый край влево. Разверните бумагу. Распечатайте цветную копию шаблона Starshade.ДжозиЛаки. Некоторые из них можно сделать к празднованию 4 июля. Экономьте на повседневных низких ценах. 8 дюймов от точки к точке. 3 доллара. Наша звезда покажет этот цвет только на многослойной спине. 6 из 5 звезд 533 Готовые звездные рождественские украшения будут составлять около 60% от размера квадрата, с которого вы начали. 99 БЕСПЛАТНАЯ доставка. (17) 1 доллар. Для этого простого оригами вам понадобятся два квадратных листа бумаги. Это оборотная сторона нашей бумаги для оригами. бумажные звезды оригами 2022 | Лучшее легкое изготовление бумажной звезды | Цветная бумага Star easy | @Cf origamiНаши новые каналы на YouTube: 25 октября 2021 г. · Оригами Звезда с квадратной бумагой — Оригами Звезда с квадратной бумагой — популярная форма, связанная в основном со складыванием бумаги.Сложить эту симпатичную звезду оригами может быть непросто, но если вы последуете по тексту, действительно ставите видео на паузу, когда это необходимо, после каждого шага, тогда у вас должно получиться 17 ноября 2015 г. · Мы любим оригами, так как вы можете сделать большинство вещей из обрезков. бумаги, в любое время и в любом месте! Это было бы отличным украшением для рукоделия 4 июля! Материалы для оригами «Звезда гнева»: 15 листов бумаги для оригами (США / Великобритания) (партнерские ссылки) (вы также можете использовать обычную бумагу для принтера или переработать газету или журналы, разрезав их на квадраты 15×15 см) «Оригами».оригами звезды из бумаги
AMS :: Математические образы: Роберт Дж. Ланг
Пересечение оригами, математики и естествознания происходит на многих уровнях и включает многие области последних. Оригами, как и музыка, также допускает композицию и исполнение как выражение искусства. За последние 50 лет я разработал около 800 оригинальных композиций оригами. Около четверти из них были опубликованы с инструкциями по складыванию, которые в оригами служат той же цели, что и партитуры: они служат руководством для исполнителя (в оригами, папка), позволяя исполнителю выразить свое мнение. собственная личность через интерпретацию и вариации.Все работы и изображения любезно предоставлены Робертом Дж. Лангом и принадлежат ему.
— Роберт Дж. Ланг
Новости : Посмотрите другие потрясающие работы оригами из бумаги — лобстера, льва, жирафа, кои и органиста — добавленные в эту галерею ниже. Кроме того, в сотрудничестве с Кевином Боксом Роберт Лэнг работал над превращением некоторых из этих творений оригами в большие памятники. Щелкните ссылку «Сотрудничество», чтобы увидеть несколько удивительных примеров из стали и бронзы.
Один неразрезанный квадрат корейской бумаги ханджи, 12 дюймов, 2004 г., композиция из серии ракообразных.
Один неразрезанный, необрезанный лист бумаги ручной работы, 12 дюймов, 2003 г., композиция из моей серии оригами млекопитающих. Классическое оригами — это «один лист, без разрезов». Но нам все равно нужно разрезать бумагу на квадрат. Или мы? На этой фигуре используется необрезанный лист бумаги ручной работы; шероховатый, неровный край декеля используется для создания гривы.
Один неразрезанный квадрат из бумаги Сен-Арман, 8 «, 2007 г., композиция из серии млекопитающих.
Один неразрезанный прямоугольник 1 ‘x 4 из бумаги Wyndstone’ Marble ‘, 6 дюймов, 1998 г., композиция из моей серии человеческих фигур.
Один неразрезанный квадрат, 15 «, 2002 г., композиция из серии рыбок оригами.
Один неразрезанный квадрат бумаги Wyndstone ‘Marble’, 8 дюймов, 2003 г., композиция из моей серии оригами млекопитающих.
Один неразрезанный квадрат Canson Mi-Teintes, 6 «, 2013. Работа, созданная на выставке DRUPA, входит в мою серию оригами млекопитающих.
Один неразрезанный квадрат бумаги оригамидо, 6 дюймов, 2003, композиция из моей серии оригами насекомых.
Один неразрезанный квадрат корейского ханджи, 6 x 6 x 15 дюймов, 2017, композиция из моей серии оригами растений и цветов.
Один неразрезанный квадрат из бумаги кодо с включениями, 8 дюймов, составлен 1988 г., сложен 2012 г.
Один неразрезанный квадрат из бумаги оригамидо, изготовленной на заказ, 12 дюймов, 2010 г. Я разработал эту композицию, чтобы продемонстрировать красоту бумаги оригамидо, которая, как мне показалось, идеально подходила к предмету. Эта фигура сложена из листа специальной партии из бумаги ручной работы, которая была изготовлена по индивидуальному заказу и вытягивается в студии Origamido под руководством и помощью мастеров-изготовителей бумаги Майкла ЛаФоссе и Ричарда Александра.
Один неразрезанный квадрат корейского ханджи, 8 дюймов, составлен в 2002 г., сложен в 2003 г.
Один неразрезанный квадрат бумаги оригамидо, 3 дюйма, сложенный и сложенный 2004
Один неразрезанный квадрат бумаги, 4 дюйма, сложенный и сложенный 2002
Один неразрезанный трехугольник из мексиканской юкки, 8 дюймов, сложенный и сложенный 2009
Один неразрезанный прямоугольник из тайской бумаги унрю, 8 дюймов, составленный и сложенный, 2008 г.
Один неразрезанный доллар, 2 дюйма, сложенный и сложенный 2010.
Один неразрезанный квадрат бумаги оригамидо, 5 дюймов, составлен в 1992 году, сложен в 2002 году.
Один неразрезанный прямоугольник корейского ханджи, 7 дюймов, 2004 г. Это экшн-модель; потяните его за голову, и он возьмется за бас.
Один неразрезанный 20-сантиметровый квадрат из дуэта красной / черной бумаги Origamido, 6 «x 2» x 4 «, 2014. Мокрая фальцовка из бумаги Origamido. Бумага имеет значение!
Один неразрезанный квадрат бумаги Canson Mi-Teintes, 7 x 3 x 6 дюймов, 2016, композиция из серии работ оригами, посвященной млекопитающим.
Один неразрезанный квадрат японской бумаги, 11 «x 3» x 5 «, 2016 г. Эта работа была написана во время поездки в Кению, а затем отредактирована и сложена после моего возвращения в Аламо.
Один неразрезанный квадрат непальской локты, составленный и сложенный в 2002 году, 6 дюймов.
Один неразрезанный квадрат бумаги оригамидо, составленный в 1993 году, сложенный в 2005 году, 5 дюймов.
Один неразрезанный квадрат акварельной бумаги, составленный и сложенный в 1996 году, 8 дюймов.
16 неразрезанных квадратов из бумаги Wyndstone «Marble», 24 дюйма.
Один неразрезанный квадрат бумаги оригамидо, сложенный и сложенный в 2004 году, 4 дюйма.
Один неразрезанный квадрат корейского ханджи, составленный и сложенный в 2003 году, 18 дюймов.
Шаблоны складок (CP) обеспечивают одноэтапное соединение развернутого квадрата в сложенную форму, сжимая сотни складок, а иногда и часы складывания в единую диаграмму! CP иногда может быть более проясняющим, чем подробная последовательность складывания, передавая не только то, «как складывать», но также то, как фигура была изначально спроектирована. Математические и геометрические CP обычно показывают все складки, но репрезентативное оригами редко показывает каждую складку в готовой форме, так как это сделало бы узор складок невозможным.Вместо этого рисунок складок дает складки, необходимые для складывания «основы», то есть геометрической формы, которая имеет правильное количество и расположение клапанов. Это все еще оставлено на усмотрение папки, чтобы добавить утончение и придание формы складкам. — Роберт Дж. Ланг
Один неразрезанный квадрат корейского ханджи, 10 дюймов, сложенный и сложенный, 2009 г.
Коробка для оригами прямоугольник
Коробка для оригами прямоугольник Инструкции по складыванию коробки для оригами · Бумага для оригами, готовая к складыванию.Не забудьте добавить выступы по бокам и на концах рисунка. 7 x 7 см. Я сделал коробку «Кокетливый фламинго» как можно больше, с «x» на 1 3/16 ″. Вы можете использовать любую бумагу, чтобы сложить коробку для оригами (* проще, если передняя и задняя стороны бумаги немного отличаются по фактуре или цвету). + При изготовлении коробки с крышкой вам нужно, чтобы внутренняя коробка была как минимум на ½ дюйма меньше (чтобы могла поместиться верхняя часть). Вы также можете превратить ее в подарочную коробку, которую вы можете подарить кому-то особенному.Иногда это называют «складкой шкафа». Вставьте одну сторону в другую. 26 октября 2021 г. · возможен треугольник, перекрещивающийся с краем бумаги. Этот закрытый прямоугольный блок начинается с матричного блока 4 x 4. Используя бумагу для вырезок, вы можете легко сделать их подходящими к теме Рождества, Пасхи, вечеринки или даже свадьбы. Сначала обрежьте лист 1212 до 8512, чтобы можно было пропустить его через принтер, а затем распечатайте шаблон на той стороне бумаги, которая должна быть внутри коробки или крышки.На главную — Книги — Схемы — Галерея — Ссылки — Видео. Прямоугольник Оригами Инструкции. Шкатулка для оригами имеет откидную крышку. Оценка 5. Как сделать бумажную коробку шаг за шагом? Эта длинная прямоугольная шкатулка для оригами начинается с основы в матрице 8×8. Узнайте, как сделать простую прямоугольную шкатулку для оригами. Как шаг за шагом сделать бумажную коробку? 28 октября 2021 г. · Эта традиционная коробка для оригами прямоугольная и сделана из прямоугольника бумаги. ) Выше на странице было показано, как сделать длинную тонкую коробку или как сделать коробку любого размера и желаемой формы.Это вид изнутри коробки. Делаем прямоугольную коробку из бумаги. Узнайте, как сделать прямоугольные коробки для оригами. Сделайте разделитель на 4, 6 или 14 секций. Загните один угол по диагонали вниз. Мы любим простые поделки из бумаги. Инструкции по началу работы с подарочной коробкой оригами, покажут вам, как сделать «нормальную» прямоугольную коробку того же размера, что и клубничная коробка на фото вверху этой страницы (длина 5 дюймов на 3 дюйма шириной на 2 дюйма высотой. квадратный кусок бумаги для оригами.Убедитесь, что бумага, которую вы используете, представляет собой квадрат (все стороны равны и все углы равны 90 градусов Прямоугольная коробка с шаблоном с крышкой Эйлин Эдвин Прямоугольная коробка для оригами с крышкой 620×454 Png Download Pngkit from www.Сложите бумагу пополам слева. Оригами Треугольник Шестиугольник Подставка под Тато Учебник. В предыдущем исследовании краш-бокс с рисунком оригами был протестирован на низкой и высокой скорости, а также при лобовом ударе и наклонном ударе. Инструкции по прямоугольной коробке оригами · начинайте складывать · сложите бумагу втрое · сложите клапан до вертикального сгиба · начните формировать коробку. Соотношение ширины, высоты и длины прямоугольника составляет 1: 1: 2. «А» (1/5) — ширина коробки. Нарисуйте глаз для прямоугольной рыбки из бумаги.центр. 6:26. Для этого не нужно использовать квадратную бумагу! Отлично подходит для складывания бумаги формата A4, A5 и Letter, а также поздравительных открыток. Они привели к предсказуемому обрушению и устойчивым моделям деформации. Бумажные коробки ручной работы — это лучшее выражение ремесел оригами. Внутренняя часть имеет размер 3 дюйма на 3 дюйма. Новый поворот в старом ящике Аннотация Цель этой статьи — описать математику, которая вытекает из конструкции шкатулки оригами. Начните цветной стороной вверх. отдельная крышка / дно не требуется.Попробуйте использовать любую бумагу по выбору, которая может быть блестящей или печатной. Сложите верх и низ этого. Легкое изготовление квадратной коробки. Этот вид показывает коробку, когда она открыта. Загните края к центральной линии. 13 ноября 2019 г. · Как создать кубик оригами: с помощью листа бумаги размером 15 х 15 см сложите его пополам по диагонали, чтобы получился треугольник. Раскройте. Как шаг за шагом сделать бумажную коробку? Готовая прямоугольная коробка. * Вам действительно не нужно печатать нижний лист. 10 июля 2012 г. · Финальную рамку можно увидеть ниже.Оригами — увлекательное искусство складывания бумаги. 00 из 5 на основании 4 оценок клиентов. Вырежьте по линиям, чтобы получить два прямоугольных листа для верхней части коробки. Если вы не хотите склеивать или сшивать его, прорежьте небольшие прорези по краям корзины и аккуратно продвиньте концы ремешка к прорезям. Узнайте, как сделать полезную прямоугольную коробку для оригами из листа бумаги формата A4 или Letter. Дата создания: эта страница предназначена для тех, кто хочет получить инструкцию по складыванию закрытой прямоугольной коробки оригами.Размер готовой коробки 4. Сложите и заправьте. Это забавная и относительно простая пошаговая инструкция по тому, как правильно складывать и складывать оригами из бумаги 11.07.2012 · Это блог о бумажных складываниях Здесь приведены инструкции, как сделать эту легкую коробку для оригами. . com Это сайт, где собраны оригами из прямоугольников, бумаги формата А4: Каждый может научиться оригами — это книга специально для начинающих, которые хотят научиться делать оригами. Если у вас есть бумага для вырезок 12 на 12 дюймов, разрежьте ее на четыре квадрата по 6 дюймов! (Чтобы вырезать бумажные квадраты).2. Прямоугольная коробка оригами. Шаг 2: Теперь сложите правую и левую стороны так, чтобы они встретились в центре. 10:10. затем можно отрезать. Складка. Подробности здесь оригами. 172onehundredandseventytwonew. Ваша форма отправлена. Храните скрепки и ластики или используйте их для сортировки украшений. Прямоугольник Оригами из бумаги Легкие инструкции по коробке для оригами. Мы собрали наши любимые идеи для прямоугольных коробок для оригами, собирающих красоту, изучите наш список популярных изображений прямоугольных коробок для оригами, собирающих красоту, и загрузите коллекцию фотографий с высоким разрешением 28 октября 2021 г. · Эта традиционная прямоугольная коробка для оригами сделана из прямоугольник из бумаги.Сложите бумагу пополам. Научитесь делать простую шкатулку-валентинку оригами. 10. Дополнительный прямоугольник бумаги вверху. 1 мая 2017 г. · Эти инструкции покажут вам, как сделать традиционную шкатулку для оригами, также известную как шкатулка масу. сложите бумагу из центра, опустите верхний клапан вниз и сделайте складку на линии, показанной ниже прямоугольной коробки оригами, шаг 8 повторите шаг 7 для верхней половины прямоугольной коробки оригами шаг 9 хорошо, мы почти закончили, инструкции подарочной коробки оригами для Crash Box прикрепленный между бампером и шасси автомобиля, служащий поглотителем кинетической энергии во время столкновения.Привет. Вытяните стороны наружу. Переверните модель и загните края по центру, согните и разверните. Прямоугольник оригами… Продолжить чтение → 2 октября 2012 г. · Я включил руководство по использованию квадратной коробки ниже (которую я использую для монет, скрепок и других канцелярских принадлежностей), но если вы хотите сделать прямоугольник, чтобы удерживать такие вещи, как карандаши и ручки, здесь есть отличный учебник с инструкциями для печати. Переверните лист цветной стороной вниз. Для 4-дюймовой коробки отмерьте 4 дюйма для стороны и 2 дюйма для концов.$ 1. Как шаг за шагом сделать бумажную коробку? Шаг 1. 18 июля, 2017 · Как сделать прямоугольную коробку для оригами с закрывающимися крышками, как сделать прямоугольную коробку из бумаги. Вы можете использовать одностороннюю цветную бумагу, как показано на рисунке ниже. Эта шкатулка для оригами отлично подходит для любых целей и имеет приличную прямоугольную форму. Повторите оба пути. Как шаг за шагом сделать бумажную коробку? 29 мая 2017 г. · Прямоугольная шкатулка для оригами своими руками — Материалы. Проекты разделены на 3 раздела: Простые коробки из квадратных листов, Модульные коробки из нескольких квадратных листов и Модульные коробки из прямоугольных листов.Вот так должна выглядеть шкатулка для оригами в сложенном виде. Коробка для оригами с крышкой. Узнайте, как сделать коробку для оригами для конфет. Девиз этого видео — поделиться легкими в изготовлении искусством и ремеслами, специально разработанными. Они отлично подойдут для детской поделки! Каждый ребенок мог сделать свою коробку и наполнить ее разными конфетами. Это очень приятно делать, и оригами — это увлекательное искусство складывания бумаги. 4:54. Инструкции по использованию прямоугольной коробки для оригами 1. 20 июня 2013 г. · Сегодня мы начнем с простой коробки для оригами, в которой можно хранить пуговицы, скрепки, канцелярские кнопки и другие мелочи.170сотенсемь новых. Складывать. На 5см меньше бумаги для крышки. Прямоугольный разделитель коробки оригами Урок 3 вида. Отлично подходит для работы с бумагой большего размера! Эту простую коробку для оригами можно сделать из газеты, вы можете использовать ее, чтобы выбрасывать обрезки во время готовки, или как мусорное ведро для пикников или поездок на автомобиле. Длинная коробка с крышкой, Оригами из подарочной коробки (Как сделать бумажную коробку) Визуальные схемы будут вам на руку. Откройте верх и низ под углом 90 градусов к основанию.Читайте дальше, чтобы узнать, как сделать сложенную бумажную коробку. При взгляде сбоку выскакивающая часть и карта образовывали квадрат. www. 29 июля 2021 г. · Коробки для Хэллоуина были ограничены квадратным размером 6 дюймов дизайнерской бумаги Cute Halloween. Это очень приятно делать и очень инструкции для прямоугольного подноса оригами. Шаблоны коробок Бесплатная печать Прямоугольник Шаблон коробки Шаблон коробки для печати Шаблон бумажной коробки Шаблон коробки 2 июня 2013 г. · Я сложил коробку с помощью 6-дюймовых (150 мм) квадратов бумаги для вырезок, 4 для крышки, 4 для основания коробки и один для внутреннего лайнера.Коробки масу изначально представляли собой квадратную деревянную коробку, которая использовалась для измерения порций риса в феодальный период в Японии. Сделайте то же самое с этой стороной. Модели этого типа также автоматически попадают в список: коробочные, геометрические, оригами-сначала, отдельные листы. Откройте и поверните на 90 °, затем снова сложите пополам. Некоторые из этих ящиков открыты с одной стороны и могут действовать как открытые контейнеры, другие могут быть закрыты с помощью петли или инструкций по прямоугольнику оригами. Оценка по размеру 5 15/16 дюйма составляет 1 3/16 дюйма, 2 3/8 дюйма, 3 9/16 дюйма и 4 3/4 дюйма.Если у вас нет квадратной бумаги, вы легко можете сделать ее из прямоугольника, просто следуйте этим или этим инструкциям. сайт Ника Робинсона. Шаблон определяет прочность и размер коробки, поэтому убедитесь, что они совпадают. Открытие или закрытие занимает менее 10 секунд. Огромное спасибо за 20 000 просмотров, как сделать шкатулку оригами с крышкой. Бумага для вырезок — моя любимая бумага для коробок. & nbsp; Видео для уклонения от кликов: 26 сентября 2021 г. · Прямоугольная коробочка-оригами. Прямоугольник оригами. Шаг 9: ОК, мы почти закончили.Сложите пополам по вертикальной оси. Коробка сделана из 2-х листов бумаги прямоугольной формы, клей не требуется. 23 июня 2014 г. · 23 июня 2014 г. Используйте лист прямоугольной бумаги. Эта категория предназначена для коробок, которые складываются из одного листа, т.е. Однолистовые коробки. Готовая прямоугольная коробка. 3 см). 5 ′ или 10. Готово. 03 мая 2020 · Я сложила любовное послание оригами. 09 июня 2020 г. · Инструкции по созданию прямоугольной коробки для оригами Инструкции по созданию прямоугольной коробки для оригами. Как шаг за шагом сделать бумажную коробку? 15 августа 2021 г. · Простое оригами из бумаги прямоугольной формы.Как шаг за шагом сделать бумажную коробку? 26 октября 2021 г. · Очень простая прямоугольная коробка с крышкой для оригами. Легкая модульная коробка для оригами. Легкая коробка для оригами. Шаг 2: Согните левый и правый край бумаги к вертикальной средней линии. бумажный квадрат «внутренней» части вашей коробки должен быть примерно 0. Эта коробка оригами отлично подходит для начинающих. С парой коробок вы можете использовать одну как коробку, а другую как крышку для упаковки небольших подарков. Прямоугольная коробка для оригами.28 октября 2021 г. · Эта традиционная коробка для оригами прямоугольная и сделана из прямоугольника бумаги. Сложите наружу по показанным складкам. Для модели 6 футов я сложил коробку из бумаги размера 4. Прямоугольная коробка оригами. Шаг 8: Повторите шаг 7 для верхней половины. Идеально подходит для тех, кто дарит подарки в последнюю минуту. От 18 л до 18 л. Разверните бумагу, а затем сложите ее пополам вниз, чтобы получился прямоугольник. Готовая шкатулка станет отличным тайником для небольших сокровищ. Это руководство покажет вам, как складывать прямоугольники из бумаги в треугольные блоки с карманами, которые используются для создания трехмерных фигур.Она толще, чем обычная бумага для оригами, что делает коробки прочными, и есть много красивых узоров, которые можно смешивать и сочетать. Поэкспериментируйте с разной толщиной, фактурой и дизайном бумаги для оригами, чтобы получить по-настоящему уникальную презентацию. Оригами-версия коробки и крышки может показаться одним из самых простых проектов оригами, но вам следует рассмотреть эту коробку для оригами и крышку в жестком режиме, как в остальном оригами для начинающих. Сначала согните пункт 4 к пункту 1. Как шаг за шагом сделать бумажную коробку? 13 июня 2021 г. · Коробка для оригами: прямоугольная — Урок — Как сделать коробку из бумаги.pngkit. Оно прямо пропорционально поглощению энергии при ударе. Начните белой стороной вверх и бумагу в альбомной ориентации. Прямоугольник оригами. Шаг 3: Сложите пополам по горизонтальной оси. 20 августа 2019 г. · Прямоугольная бумага для оригами Us 132 20 Off50pcset Квадратная бумага для оригами с односторонней блестящей складной однотонной блестящей бумагой для детей. Прямоугольник оригами. Шаг 6: Теперь загните верхний правый и левый углы до вертикальной складки. Бесплатные инструкции по рукоделию, оригами и бумажному искусству на День святого Валентина.Как шаг за шагом сделать бумажную коробку? Прямоугольная коробка оригами. Чтобы сделать эту красивую, необычную коробочку, я использовала бумагу Designer Series размером 12 x 12 дюймов. Простая квадратная коробка оригами Новый поворот в старой коробке Аннотация Цель этой статьи — описать математику, которая вытекает из конструкции коробки оригами. коробка для оригами прямоугольник
Упаковка и установка Soft Origami в цилиндрические объемы и их применение в автомобильных подушках безопасности
R Soc Open Sci. 2016 сен; 3 (9): 160429.
Кафедра машиностроения, Университет Бригама Янга, Прово, UT 84602, США
Поступила в редакцию 23 июня 2016 г .; Принято 25 августа 2016 г.
Опубликовано Королевским обществом в соответствии с условиями лицензии Creative Commons Attribution License http://creativecommons.org/licenses/by/4.0/, которая разрешает неограниченное использование при условии указания автора и источника. статья процитирована другими статьями в PMC.Abstract
Упаковка мягких листовых материалов с приблизительно нулевой жесткостью на изгиб с использованием Soft Origami (шаблоны оригами, применяемые к мягким листовым материалам) в цилиндрические объемы и их развертывание с помощью механизмов или внутреннего давления (надувания) представляет интерес в областях, включая автомобильные подушки безопасности, развертываемые сердечные стенты, надувные космические жилища, дирижабль и парашютный снаряд.В этой статье исследуются двойные модели, «мигалка» и «перевернутый конус», для упаковки мягких листовых материалов в цилиндрические объемы. Два способа и механизма первоначальной упаковки исследуются для каждого из шаблонов складывания «перевернутый конус» и «перевернутый конус». Выполняется приложение к автомобильным подушкам безопасности со стороны водителя, и завершаются тесты развертывания для сравнения влияния метода упаковки и рисунка оригами на эффективность развертывания. После испытаний на развертывание изучаются два дополнительных метода упаковки для модели сгиба в виде перевернутого конуса, которые применяются к автомобильным подушкам безопасности.Показано, что изменение метода упаковки (использование разных методов для наложения одного и того же базового рисунка на материал мягких листов) может привести к разным характеристикам развертывания. В общей сложности исследуются два выкройки оригами и шесть способов упаковки, а также обсуждаются преимущества использования выкроек мягкого оригами и методов упаковки. Мягкое оригами представлено как жизнеспособный метод для эффективной упаковки материалов из мягких листов в цилиндрические объемы.
Ключевые слова: Soft Origami, складывание ткани, цилиндрическая упаковка, подушка безопасности, надувные лодки
1.Введение и предыстория
Упаковка и развертывание мягкого оригами (материалы из мягких листов, сложенных в узоры оригами) в цилиндрические объемы и из них представляет интерес в отраслях, где гибкий лист материала должен вписаться в ограниченную цилиндрическую форму перед развертыванием через механизмы или внутреннее давление.
Для целей данного исследования материал с мягкими листами определяется как материал постоянной толщины с приблизительно нулевой жесткостью на изгиб (например, текстиль, ткани и тонколистовые полимеры).Мягкие листовые материалы легко мнутся, сгибаются и мнутся локально, что может быть полезно при использовании их с узорами сгиба оригами.
1.1. Оригами и инженерное проектирование
Применение узоров, извлеченных из оригами или вдохновленных им, в инженерном дизайне может вдохновить на новые подходы к проблемам дизайна. Возможные преимущества применения оригами в инженерном проектировании включают предсказуемое развертывание, компактную упаковку и большое количество доступных шаблонов. В предыдущих исследованиях изучались приложения жестко-складываемых узоров и методы нанесения узоров оригами на материалы толще бумаги [1–3], использование мигающих узоров для космических приложений [4], создание складывающихся поверхностей и других узоров, основанных на криволинейном складывании. оригами [5–7], проектирование развертываемых конструкций укрытий [8], проектирование развертываемых цилиндрических конструкций и мачт [9–12], использование вычислительных методов для разработки сложных схем и форм складок [13,14] и общие методы выбора выкройки оригами и их применение в задачах проектирования [15].
Еще одна тема, которая рассматривалась в оригами и инженерии, — это масштабируемая и легко настраиваемая упаковка и разработка шаблонов. Если дизайнерам необходимо приспособить общий узор (который может быть увеличен или уменьшен пропорционально) в конкретный контейнер или упакованную форму, эта характеристика особенно ценится, и оригами предоставляет метод для создания таких масштабируемых дизайнов. Примеры масштабируемой упаковки и дизайна рисунка в области цилиндрических конструкций включают развертываемые солнечные батареи [4], сердечные стенты [16] и систему поддержки структуры сердца для пациентов, страдающих сердечной недостаточностью [17].
1.2. Мягкое оригами и использование материалов из мягких листов
Использование материалов из мягких листов с узорами оригами подпадает под действие «Мягкого оригами», основанного на качественном понимании соответствия используемых материалов из мягких листов узорам оригами. Мягкое оригами недавно было изучено как метод применения методов дизайна оригами к гибким материалам или субстратам, с потенциальными приложениями в биоинженерии (например, трехмерные каркасы из ткани), гибкой электронике и других приложениях, где требуются или полезны шарниры с высокой степенью совместимости, и это желательно накладывать узор оригами с незначительным усилием [18].Использование выкроек оригами является ценным подходом из-за возможности упаковать материалы из мягких листов в желаемое упакованное положение и впоследствии развернуть их из этого положения. Поскольку мягкие листовые материалы чрезвычайно податливы и могут локально сминаться, сгибаться и складываться для обеспечения неточного складывания линий сгиба рисунка оригами, не требуется строго определенных линий сгиба или «петель», что упрощает производство. Soft Origami дает возможные преимущества в таких областях, как производство и упаковка подушек безопасности, проектирование и изготовление воздушных фильтров, упаковка и развертывание парашютов, проектирование разворачиваемых надутых конструкций (включая надувные космические среды обитания, такие как модуль BEAM, установленный в 2016 году на Международной космической станции [19–22]. ]), надувные гидроциклы, надувные индивидуальные аттракционы (батуты, горки и воздушные шары), упаковка для палаток, упаковка и развертывание зонтов, навесы (например.грамм. путевые палатки) и упаковка аварийных одеял.
Производительность развертывания также требует рассмотрения при применении Soft Origami для решения задач проектирования. В некоторых случаях развертывание будет происходить много раз в течение срока службы продукта (например, палатка для кемпинга), а в других развертывание произойдет только один раз (например, автомобильные подушки безопасности). В зависимости от того, насколько критичной является производительность повторного развертывания, при выборе шаблонов упаковки необходимо соблюдать разные уровни осторожности. В таких случаях, как автомобильные подушки безопасности и парашюты, где человеческая жизнь зависит от точного развертывания конструкции, обширное тестирование и доработка являются ключевыми для обеспечения того, чтобы характеристики окончательного развертывания соответствовали требуемым стандартам.Предыдущие вычислительные методы для трехмерного складывания подушек безопасности были признаны успешными, но они требуют больших вычислительных ресурсов [23]. В других случаях для достижения одной и той же цели может использоваться множество различных рисунков, если конечный упакованный продукт помещается в требуемое пространство или упаковку (например, палатка в сумке для палатки, зонт в сумке для хранения, аварийное одеяло в упаковке для хранения). . В приложениях, где развертывание происходит за счет перепада давления (например, при заполнении воздухом или другим газом) и где продукты не могут иметь внутри жестких элементов по соображениям безопасности (например,грамм. подушки безопасности), важнейшее требование, которому могут соответствовать Soft Origami и материалы из мягких листов, — это метод упаковки, при котором любые жесткие элементы, используемые в процессе складывания, удаляются до того, как продукт станет функциональным или развернутым. Это позволяет спроектировать преднамеренную последовательность развертывания (с помощью навязанного рисунка оригами), не требуя при этом опасных внутренних жестких механизмов внутри продукта, и добавляет к преимуществам использования мягких оригами и материалов из мягких листов.
1.3. Цель
В этом исследовании рассматриваются схемы сгиба и методы упаковки, которые эффективно упаковывают материалы из мягких листов с использованием методов мягкого оригами в цилиндрические упакованные формы с настраиваемой высотой и диаметром в сложенном (упакованном) виде, развернутой (развернутой) формой и развернутым размером.Также исследуются производительность развертывания и влияние метода упаковки на развертывание. Двойные узоры и связанные с ними методы упаковки исследуются как потенциальные решения для упаковки мягкого листового материала в желаемую цилиндрическую форму. В качестве демонстрации эти образцы и методы упаковки применяются к тематическому исследованию автомобильных подушек безопасности, а также рассматриваются и сравниваются характеристики развертывания.
2. Цилиндрическая упаковка и развертывание
Один из распространенных в настоящее время методов, используемых для упаковки мягкого листового материала в цилиндр, заключается в прямом сжатии мягкого листового материала в желаемую упакованную форму и контейнер без определенных форм складывания (аналогично тому, как спальный мешок часто помещают в цилиндрический «мешок для вещей»).Однако этот метод может привести к непредсказуемости развертывания. В зависимости от приложения это может быть приемлемым или неприемлемым. Существуют и другие основные схемы складывания (например, метод складывания втрое, обычно используемый для складывания палаток, когда объект складывается, как брошюра, сложенная втрое, перед свертыванием материала в плотно упакованный цилиндр), которых может быть достаточно в зависимости от заявление. В этом исследовании предлагаются два шаблона оригами, которые можно применить к материалам из мягких листов для достижения аналогичной формы и размера в упаковке, но с учетом различных характеристик развертывания, и показано, что конкретные желаемые характеристики развертывания могут быть продиктованы изменением методов упаковки (складывания).
Требуемые параметры для окончательной формы упаковки — это диаметр D и высота H цилиндра, описанного вокруг сложенного шаблона, показанного на. В следующих подразделах представлены наш выбор шаблона, методы упаковки и рекомендации по развертыванию. Шаблоны оригами используются в этом исследовании как механизм для общего прогнозирования формы упаковки и характеристик развертывания.
Нераскрытый образец мигалки с цилиндрической оболочкой вокруг него.Указанная высота H и диаметр D представляют интерес.
2.1. Выбор и моделирование шаблонов
Поиск шаблонов оригами был проведен с акцентом на поиск шаблонов, которые складываются в в целом цилиндрическую форму и могут быть смоделированы и изменены математически. Эти узоры включали в себя шестигранную модель оригами-мигалки, Миуру, Арк-Миуру и коническую Миуру [24], цилиндрический узор Креслинга [10], магический шар водяной бомбы [25] и узор складного зонта.
Некоторые из этих шаблонов плохо масштабируются до разной высоты. То есть некоторые (например, дуга-Миура) не сжимаются в обоих направлениях (радиальном и осевом) при раскрытии. Для этих шаблонов, если развернутая структура должна иметь определенную упакованную высоту, упакованная высота такая же, как у развернутой структуры. В результате образцы, которые плохо масштабируются до разной высоты упаковки (например, Miura и производные), не были выбраны для этого исследования.
Два шаблона были выбраны на основе их реконфигурируемости и способности плотно упаковываться в цилиндр: мигалка и шаблоны «сгиб зонтика».Образец мигания, показанный на, желателен из-за его масштабируемой высоты и развернутой площади поверхности, формы и размера. Поскольку существуют жестко складываемые версии мигалок [26], мы можем создать метод, использующий устройства для складывания жестких панелей, для складывания мягкого листового материала в плотно упакованный цилиндр с возможностью выбора конкретных размеров, таких как высота в упаковке и диаметр в развернутом состоянии. . «Зонтичная складка», также желательная из-за ее масштабируемой высоты и конфигурируемой площади развернутой поверхности и формы, представляет собой материал мягкого листа, приближенный к разворачивающейся модели изогнутой складки поверхности, инверсии конуса [5,27], показанной на рис.Разворачивающийся перевернутый конус, существующий в складке зонта, показан в b вместе с полупрозрачной накладкой обычного зонта. Этот узор или его варианты ранее использовались в произведениях искусства [28]. В частности, это простая версия развертываемого поверхностного рисунка, в котором конус несколько раз перевернут между вершиной и основанием. Чтобы отличить этот конкретный узор от других узоров, которые используются для складывания зонтов, этот узор (при складывании из мягких листовых материалов) будет называться «складкой в виде перевернутого конуса».Версия с изогнутой складкой, показанная в a , имеет некоторый конечный угол между перевернутыми слоями и в результате не может сжиматься в цилиндр. Использование мягких листовых материалов позволяет нам сжать узор за пределами конечного угла версии с изогнутой складкой в компактный цилиндр.
Развертка флешера ( a ) и физический прототип матовой доски с пластиковым несущим шарнирным слоем на различных стадиях развертывания ( b ).
Сгиб в виде перевернутого конуса ( a ) узор оригами с изогнутым сгибом и трехмерная модель с изображением зонтика с перевернутым конусом ( b ), наложенная на форму сгиба в виде перевернутого конуса.
Выбранные шаблоны позволяют изменять площадь поверхности, размер и форму, а также высоту в упаковке. Изменяя выбранные параметры каждого шаблона, можно создать почти бесконечное количество вариаций, которые упаковываются и развертываются желаемым образом. Когда эти рисунки накладываются на материалы с мягкими листами, материалы могут быть сжаты до приблизительно цилиндрической упакованной формы. Эта особенность является наиболее важным фактором при выборе этих двух паттернов для дальнейшего изучения.В следующем разделе исследуются возможные методы производства (упаковки) для нанесения обоих рисунков на мягкие листовые материалы.
2.2. Способы упаковки
Выкройки оригами были использованы в качестве вдохновения для создания методов упаковки материалов из мягких листов в выбранные выкройки. Ниже описаны индивидуальные методы упаковки для каждого рисунка.
2.2.1. Flasher
Шаблон сгиба мигалкой, на котором показаны узор и физический прототип, состоит из шаблона оригами, который можно переконфигурировать, чтобы упаковать его по форме, близкой к цилиндру.В качестве примера использован шестиугольный мигающий светильник с изменяемой высотой и развернутой формой. Хотя здесь показан шестиугольный узор, возможны и другие многоугольные формы. Этот образец ранее применялся к космическим солнечным батареям с использованием методов размещения по толщине [4] и других приложений, где желательна форма от большой развернутой площади до упакованной. Еще одно преимущество флешера заключается в том, что мягкий листовой материал сжимается одинаково в радиальном направлении во всех точках по окружности материала, поэтому не остается неровных створок, как это бывает с обычным складным зонтом.
Один из возможных методов упаковки для шаблона складывания фальцовки заключается в использовании всплывающего устройства, такого как тот, который сделан из матового картона, показанного в виде складывающейся конструкции с мягким материалом поверх нее; материал складывается в форму мигалки поверх конструкции, а затем удаляется. Разновидностью этого метода упаковки является использование двух складных столов с материалом, зажатым между ними. Второй метод — создать серию жестких звеньев, которые должны складываться тем же способом, что и флешер.
2.2.2. Сгиб в виде перевернутого конуса
Образец сгиба в виде перевернутого конуса показан на позициях a . Это серия конусов разного диаметра, которые были последовательно перевернуты, в результате чего получается массив концентрических колец, если смотреть сверху, и также упоминается как инверсия разворачивающегося поверхностного конуса [29]. Хотя на показанном здесь рисунке есть только одна долина и одна горная складка между центральной вершиной и внешним краем, можно добавить больше колец, чтобы увеличить диаметр формы.Эта изогнутая складка использовалась много лет, особенно в качестве искусства. Вариации (многие из которых являются более сложными) этого рисунка можно увидеть в работе Рона Реша «Целующиеся желтые шишки», а также в нескольких пьесах Дэвида Хаффмана, таких как «Конус отражается 7 раз» и пьесах Хироши Огавы [6] .
Если полностью разворачивающийся узор в виде перевернутого конуса изготовлен из мягкого листового материала, который может локально сморщиваться, сгибаться и сгибаться, этот узор пригоден для создания уплотненной цилиндрической формы, у которой исходная форма, размер поверхности, диаметр, конечная высота упаковки и упакованный диаметр можно выбрать.Использование материала, который может локально сморщиваться, сгибаться и складываться, позволяет нам использовать «скелет» формы разворачивающегося конуса, перевернув его, чтобы сложить ткань. «Каркас» механизма жестких звеньев может быть создан на основе изогнутого рисунка складок, который может быть использован для складывания материалов из мягких листов в форме, близкой к цилиндру. Жесткий механизм, используемый для складывания, можно снять перед развертыванием.
Существует несколько вариантов изготовления или складывания мягкого листового материала в виде перевернутого конуса.Один метод был основан на обычном механизме складывания складных зонтов. Складные зонты обычно имеют ряд жестких звеньев, которые контролируют ткань (мягкий листовой материал). Так как ткань может локально морщиться, сгибаться и складываться, примерная инверсия конуса может изменяться от полностью упакованной до открытой, в отличие от версии с немягким листовым материалом. Как правило, зонт не становится полностью плоским в открытом состоянии (скорее, он имеет наклонную форму, чтобы вода стекала по внешнему краю). Жесткие звенья, наложенные на складку перевернутого конуса с двумя внешними кольцами, показаны на разворачивающейся поверхности перевернутым конусом криволинейной складки в.Длину звеньев можно масштабировать для достижения заданной высоты в упаковке, а количество слоев определяет площадь и размер развернутой поверхности. Разработчик может изменить количество слоев и высоту слоев, чтобы получить легко реконфигурируемые упакованные и развернутые размеры. Существует компромисс между количеством слоев (количество колец, если смотреть сверху) и диаметром упаковки. В частности, каждое кольцо добавляет по меньшей мере 4 t общей толщины к диаметру, где t — толщина материала.
Перевернутый конус ( a ) жесткие звенья (похожие на зонтик), которые позволяют зонту, сделанному из растяжимой ткани, переходить из полностью открытого в полностью закрытое положение, и ( b ) два различных варианта конфигурации спиц.
В случае зонта звенья соответствуют линией, присущей разворачивающейся поверхности конуса инверсии [30]. Если число звеньев, соответствующих линяющим линиям, увеличить до бесконечности, линии будут приближаться к форме разворачивающейся поверхности инверсии конуса.Однако существует физический предел из-за размера и вмешательства необходимых рычагов. Наличие некоторого количества равномерно расположенных «спиц», которые используются в качестве механизмов складывания, является потенциальным способом производства, и большее количество спиц может привести к более точному шаблону сгиба, как показано в b .
Используя идею спиц, были исследованы два различных метода производства, показанные на. Каждый из них может быть выполнен с любым желаемым количеством спиц, превышающим три, в соответствии с физическими производственными ограничениями.Четыре спицы использовались в физических прототипах, которые были созданы. Первый способ изготовления заключается в использовании рычажного механизма, аналогичного наложению рычага, ранее показанному на позициях и . a подробно описывает эту связь, в которой ткань укладывается поверх спиц механизма, закрепляется с помощью всасывания или слабого сцепления, а затем связь складывается. В этом случае высота H сложенного шаблона будет примерно равна длине каждого звена. Одним из распространенных механизмов, который можно было бы приспособить для этой цели, является ножничная связь, которая уменьшит требуемые степени свободы по сравнению с показанным механизмом связи.Из-за дискретного характера спиц, используемых в этом методе, будут возникать остатки закрылков, которые необходимо обработать (показаны на), которые минимизируются за счет увеличения количества спиц.
Способы складывания перевернутого конуса: ( a ) метод упаковки рычажного механизма, при котором ткань накладывается на рычажный механизм, образованный жесткими звеньями, где высота H упаковки может быть выбрана путем выбора желаемой длины звеньев и механизм можно вынуть из материала по окончании складывания; ( b ) Метод упаковки механизма ползуна, при котором ткань укладывается поверх сборки ползуна на этапе 1 и складывается в слои, выполняя этапы 2–4.В обоих ( a ) и ( b ) конечная высота в упаковке H механизма равна длине звеньев и ползунов, соответственно.
Сгиб в виде перевернутого конуса, показанный в середине процесса складывания. Обратите внимание на свободные отвороты ткани, которые затем оборачиваются вокруг центральной части, чтобы получить цилиндрическую набивку.
Второй потенциальный способ изготовления для выполнения того же сгиба — использование механизмов ползуна для спиц, как показано в b .В этом методе ткань продвигается вниз между ползунками постепенно, при этом каждый ползунок прижимает ее к предыдущему (более внутреннему). Высота упакованного рисунка будет примерно равна высоте ползунков. У этого выкройки будут похожие остатки ткани.
Один из способов учесть остатки закрылков, образовавшиеся в результате обоих методов, — это обернуть их по часовой стрелке или против часовой стрелки вокруг уплотненной формы, подобно складному зонту.После того, как произошло сгибание, складывающуюся рамку можно снять с уплотненной ткани перед упаковкой ткани в цилиндрический корпус, обернув оставшиеся клапаны вокруг центральной части и закрепив складку ограничителем.
2.3. Вращение развертывания
При использовании Soft Origami вращение может происходить во время развертывания. При использовании шаблонов складывания мигалки и перевернутого конуса основным предиктором поворота развертывания является то, были ли клапаны материала обернуты по круговой схеме на любом этапе процесса упаковки.В случае мигающего рисунка, когда рисунок складывается вверх, каждая часть мягкого листового материала испытывает вращение из-за природы основного мигающего рисунка, что можно увидеть на трех этапах развертывания. Упакованный флешер Soft Origami будет вращаться при развертывании во время движения, обратного его складыванию. В зависимости от того, как была упакована складка в виде перевернутого конуса, вращение может происходить, а может и не быть. Если есть оставшиеся закрылки, которые необходимо обернуть вокруг центральной части, как показано на, при раскрытии произойдет соответствующее вращение.
3. Применение: автомобильные подушки безопасности
Боковые подушки безопасности водителя ранее имели форму прямоугольной призмы, а форма рулевого колеса была разработана таким образом, чтобы подходить к блоку подушки безопасности. Последние тенденции указывают на то, что автопроизводители используют цилиндрические рулевые колонки и цилиндрические центральные части рулевых колес. В результате современные схемы сгиба были изменены, чтобы соответствовать цилиндрическим креплениям вместо прямоугольных, что привело к неидеальному использованию пространства из-за зазоров по краям.Другой подход, который был успешно использован, представляет собой сгибание сжатия, при котором подушка безопасности сжимается до цилиндрической формы с использованием цилиндрической формы и тысячи фунтов приложенной силы. Базовый узор, который больше напоминает цилиндр, представляет интерес для повышения эффективности упаковки. Таким образом, подушки безопасности являются ярким примером мягкого листового материала, который необходимо сложить в цилиндр и который имеет критические характеристики раскрытия.
В сотрудничестве с Autoliv, производителем автомобильных подушек безопасности, на трех модулях боковой подушки безопасности водителя были наложены схемы складывания перевернутого конуса и мигалки, которые были развернуты с использованием стандартных процедур испытаний.Исходный (базовый) узор сгиба показан в b , где прямоугольный призматический узор сгиба упакован в цилиндрическую форму. Эффективность цилиндрической набивки и характеристики развертывания были протестированы для сравнения различных складок с базовой линией. В этой заявке было проведено сравнение «используемого пространства мешка для упаковки» или высоты пространства, доступного для инфлятора (газогенерирующего устройства, которое обычно представляет собой металлический цилиндр), который должен быть вставлен в заднюю часть модуля подушки безопасности после упаковки. также выполнил.
Вид сверху ( a ) мигающего рисунка, наложенного на подушку безопасности в корпусе, упакованном с использованием жесткого складного стола из матового картона и гибкой шарнирной основы для мигающего рисунка, ( b ) базовый сгиб, наложенный на подушку безопасности в корпус, сложенный с использованием традиционного прямоугольного сгиба, углы которого сжимаются или сжимаются внутрь, чтобы соответствовать круговому периметру корпуса подушки безопасности, и ( c ) сгиб в виде перевернутого конуса, наложенный на подушку безопасности в корпусе, упакованный с использованием четырех механизмы слайдера для схемы сгиба в виде перевернутого конуса.Перед съемкой все шаблоны были сжаты до одинаковой высоты. Обратите внимание на черный корпус, видимый под ( a ) и ( c ), но не ( b ), что предварительно указывает на более эффективную цилиндрическую набивку для мигалок и шаблонов с перевернутым конусом.
3.1. Применяемые методы упаковки
Вышеупомянутые методы упаковки применялись к боковым подушкам безопасности водителя автомобиля, состоящим из двух круглых дисков из мягкого листового материала, сшитых вместе по внешнему краю и имеющих инфлятор, вставленный через центральное отверстие в нижнем слое материала.Нейлоновые подушки безопасности толщиной примерно 0,25 мм на слой были упакованы в цилиндрическое крепление диаметром 122 мм и высотой 57 мм.
3.1.1. Flasher
Метод складного стола был применен к подушке безопасности, чтобы придать шаблону мигания цилиндрическую форму, упомянутую выше. В этом случае складной стол, сделанный из жестких панелей матового картона, приклеенных к гибкой подложке (чтобы действовать как петли вдоль линий сгиба), был создан из расчетных размеров, соответствующих желаемой высоте и диаметру в сложенном состоянии.Сложенная подушка безопасности с нанесенным на нее шаблоном мигания показана в a со сравнительным изображением базовой линии сгиба в b . Фальц сгиба показывает повышение эффективности цилиндрической насадки. Учитывая, насколько хорошо складка мигалки остается в границах крепления по сравнению с базовой складкой, наблюдается заметное улучшение. Пространства для пакетов мешков не были эквивалентными, поскольку складывающаяся складка обеспечивала на 2,5 мм (10%) меньше места для упаковки мешков, как показано на рис. Из-за того, что объем мешка для упаковки был хуже, складывание-мигалка дало неоднозначные результаты, так как требовалось эффективно вписаться в цилиндрическое пространство в этом конкретном приложении.
Таблица 1.
Сравнение объема мешка в пакете (высота пространства, доступного для инфлятора, который должен быть вставлен в заднюю часть модуля подушки безопасности после упаковки) для базовой линии, складывания перевернутым конусом и складывания мигалкой.
| складка | место для мешка (высота, мм) | % меньше базового |
|---|---|---|
| базовое | 26 | 0 |
| 62 | перевернутый конус | перевернутый конус8|
| фальцевальная заглушка | 23,5 | 10 |
3.1.2. Складывание перевернутого конуса
Метод ползунка был применен к подушке безопасности, чтобы придать ей цилиндрическую форму, получившаяся подушка безопасности показана в c , наряду со сравнением базовой линии сгиба в b . Для этого прототипа лишние створки, оставшиеся при использовании механизма складывания с четырьмя спицами, были обернуты по часовой стрелке вокруг остальной части подушки безопасности после снятия со складывающейся рамы.При осмотре складка в виде перевернутого конуса показывает повышение эффективности цилиндрической насадки. Одно из сравнений — оценить, насколько хорошо складка в виде перевернутого конуса остается в пределах границ крепления. В случае сгиба базовой линии внешний край крепления виден только в нескольких местах из-за того, что сложенная подушка безопасности нависает над внешним краем формы. Кроме того, высота упаковки была примерно одинаковой, а складка в виде перевернутого конуса обеспечивала только на 0,2 мм (0,8%) меньше места для упаковки, как показано на рис.
3.2. Характеристики срабатывания
Модули подушек безопасности были протестированы в испытательных центрах подушек безопасности в сотрудничестве с Autoliv. показывает изображения, сделанные с использованием высокоскоростного видео. Тесты проводились при температуре окружающей среды (комнатной) и следовали стандартным протоколам тестирования развертывания. Желательные характеристики развертывания были отмечены и наблюдались в каждом тесте. Некоторые из наиболее важных характеристик, такие как центральная панель подушки безопасности, представляющая себя первой для пассажира, а также минимальное вращение при срабатывании, тщательно отслеживались.Чтобы сравнить вращение подушек безопасности, на каждую фотографию были добавлены центральные линии, где видна центральная панель, чтобы сделать сравнение вращений более удобным.
Изображения троекратных схем, реализованных в подушках безопасности в реальных тестах развертывания. Шаблоны включают базовую складку, мигающую складку и складку перевернутого конуса. Осевые линии наложены, чтобы показать ориентацию центральной панели. Столбцы представляют разные рисунки сгиба, как указано на этикетке. Строки представляют три разных момента времени: 1–8 мс; 2–11.25 мс; 3–22,25 мс. Изображения делались в моменты, когда можно было сравнить важные характеристики развертывания. Все изображения были получены в сотрудничестве с Autoliv.
3.2.1. Флешер
При сравнении производительности флешера ( F ) с базовым уровнем ( B ) во время 1 (8 мс) наблюдается различное состояние развертывания в B1 (базовый шаблон) и F1 (шаблон флешера). F1 все еще имеет цилиндрическую упакованную форму и начал расширяться наружу (в сторону камеры), но не радиально.
Продолжая сравнение во время 2 (11,25 мс), большая часть радиального развертывания произошла в базовой схеме в B2, в то время как сложенная подушка безопасности с мигалкой в F2 не развернулась достаточно далеко в радиальном направлении, чтобы центральная панель была четко видна. F2 также показывает нежелательное вращение, заедание и взбивание при открытии.
В момент времени 3 (22,25 мс) B3 завершил развертывание и стабилизировался по желанию. F3 едва развернута полностью, скручена и не по центру. Следуя показанным здесь кадрам, F3 полностью стабилизировалась не ранее, чем через 30 мс.
Анализ результатов, проведенный персоналом Autoliv после нескольких испытаний, включая испытание, представленное в, пришел к выводу, что образец мигающего сигнала, демонстрируя многообещающую эффективность цилиндрического набивки, подвергался вращению приблизительно на 180 °, что нежелательно для применения с подушками безопасности. Он также не разворачивался достаточно быстро в радиальном направлении и не представлял свою центральную панель так быстро, как хотелось бы. По этим причинам необходима дополнительная работа, прежде чем он станет жизнеспособным вариантом складывания для установки с боковой подушкой безопасности водителя.Из-за низкой производительности в этом приложении фальцовка флешера была исключена из рассмотрения по мере продвижения исследований.
3.2.2. Складывание перевернутого конуса
Сравнивая характеристики перевернутого конуса ( IC ) с базовым уровнем ( B ) в момент времени 1 (8 мс), мы видим аналогичное развертывание в B1 (базовый образец) и IC1 (перевернутый конус шаблон). И B1, и IC1 демонстрируют благоприятное представление центральной панели (синий прямоугольный контур в центре) и аналогичную хорошую прогрессию развертывания.
Продолжая сравнение во время 2 (11,25 мс), мы видим, что большая часть радиального срабатывания произошла в базовой схеме в B2, в то время как подушка безопасности с перевернутым конусом в IC2 демонстрирует сходство, но немного отстает и демонстрирует меньшее — чем идеальное радиальное развертывание. В частности, B2 показывает более круговое развертывание, в то время как IC2 развертывается в слегка овальной форме.
В момент времени 3 (22,25 мс) B3 завершил развертывание и стабилизировался по желанию. IC3 немного отстает в своем развертывании, и хотя он полностью развернут в радиальном направлении (он представляет собой полностью круглую переднюю панель), можно увидеть, что центральная панель повернута по сравнению с B3.Это вращение показывает, что оно не полностью стабильно. Следуя показанным здесь кадрам, IC3 не полностью стабилизировался примерно до 38 мс, значительно позже допустимого предела времени для стабилизации. В целом, он работал аналогично базовой модели, но показал некоторые неблагоприятные проблемы с вращением и стабилизацией.
Анализ результатов персоналом Autoliv после нескольких тестов, включая тест, показанный в, пришел к выводу, что складывание перевернутого конуса работает лучше, чем мигалка. Он показал хорошее радиальное развертывание и многообещающую скорость развертывания и максимально приблизился к базовой схеме.Тем не менее, он показал нежелательный поворот на 90 °, который следует минимизировать, прежде чем его можно будет внедрить в коммерческие подушки безопасности. Одна из причин такого поворота заключается в том, что процесс складывания приводит к тому, что несколько частей мешка не упаковываются в исходный цилиндр (клапаны, которые выдвигаются после того, как ползун или механизмы звеньев ползуна используются для сжатия материала к центру), и вместо этого их необходимо сдвинуть. обернутый вокруг центральной формы, чтобы поместиться (что приводит к вращению при разворачивании). Это аналогично обертыванию оставшейся ткани вокруг складного зонта, когда руки сложены, а затем закреплению обернутой ткани ремнем.показывает изображение подушки безопасности на этом этапе процесса складывания. Основываясь на многообещающих характеристиках и оценке складки перевернутого конуса, дальнейшие исследования были сосредоточены исключительно на улучшении характеристик этой модели.
3.3. Модификация метода упаковки на основе производительности развертывания
Для повышения производительности развертывания были созданы новые методы упаковки для складки перевернутого конуса, чтобы минимизировать проблемы с вращением. Шаблоны остаются прежними, но можно использовать новые методы для достижения производительности, близкой к желаемой функции этого конкретного приложения.Хотя следующие методы могут использоваться для улучшения характеристик раскрытия подушки безопасности, другие методы могут быть более подходящими для различных применений. Одним из основных преимуществ использования Soft Origami является то, что один и тот же базовый шаблон можно использовать с разными методами упаковки для достижения разной производительности развертывания.
Два новых метода упаковки были созданы для упаковки перевернутого конуса таким образом, чтобы уменьшить вращательное вращение при развертывании. Первый новый метод упаковки называется методом перекрестного смещения и направлен на увеличение дискретности складок, то есть на увеличение количества спиц (упомянутых в § 2 и показанных в b ).В этом случае восемь спиц использовались для уменьшения размера закрылков, тем самым сводя к минимуму уровень результирующего вращения при раскрытии. Устройство для этого метода состоит из двух поперечных механизмов и двух панелей, показанных на позициях и . В этом методе подушка безопасности укладывается между панелями, и первая крестовина вставляется снизу в нижние прорези для создания первого сгиба. Затем приводится в действие крест, чтобы сжать складку по направлению к центру. Затем вторая крестовина вставляется сверху в противоположную панель со смещением 45 ° и приводится в действие тем же способом.Затем снимается первая крестовина, и процесс повторяется до полного складывания подушки безопасности. b дополнительно изображает характер смещения пазов панели и движение поперечных лопастей.
Механизм перекрестного смещения и последовательность складывания, с ( a ) изометрическим видом механизма перекрестного смещения. Высота H упакованного рисунка может быть выбрана путем выбора желаемого смещения между верхней и нижней панелями. Обратите внимание на два набора крестообразных механизмов, каждый с четырьмя скользящими механизмами, с верхним поперечным смещением на 45 ° относительно низа, которые поочередно вставляются в панели сверху и снизу и используются для упаковки шаблона сгиба в виде перевернутого конуса.В ( b ) мы видим вид сверху образца последовательности сгибов, где первый набор сгибов накладывается в одном направлении, а затем второй набор сгибов смещен на 45 °, таким образом увеличивая дискретность сгиба и уменьшая размер оставшихся закрылков.
Этот метод был разработан в первую очередь из-за его способности уменьшать размер лоскута, но также из-за его возможности автоматизации. Восемь широких лопастей (сверху и снизу) повторно используются для каждой складки, что значительно уменьшает количество степеней свободы складывающего устройства.Складка в виде перевернутого конуса была применена к подушке безопасности того же стиля, размера и материала, что и использованная в базовой модели. Это показано в a вместе со сравнением базовой складки в b . Для этого прототипа оставшиеся закрылки с правой стороны были завернуты по часовой стрелке, а закрылки слева — против часовой стрелки. Обратите внимание, что этот метод является только дискретной версией складки перевернутого конуса, и с большим количеством лопастей он приведет к окончательному уплотненному состоянию, которое больше напоминает складку перевернутого конуса, и, кроме того, будет иметь меньший размер клапана.Эффективность упаковки была аналогична базовой, но ожидается, что она будет улучшена с помощью хорошо разработанного фальцевального устройства.
Вид сверху ( a ) сгиба перевернутого конуса, наложенного на подушку безопасности в корпусе, упакованном с использованием описанного перекрестного метода смещения для образца сгиба перевернутого конуса, ( b ) сгиб базовой линии, накладываемый на подушку безопасности в корпус, сложенный с использованием традиционного прямоугольного сгиба, углы которого сжаты или согнуты внутрь, чтобы соответствовать круговому периметру корпуса подушки безопасности, и ( c ) сгиб в виде перевернутого конуса, наложенный на подушку безопасности в корпусе, упакованный с использованием описанного метод вложенного цилиндра для шаблона сгиба в виде перевернутого конуса.Перед съемкой все шаблоны были сжаты до одинаковой высоты. Обратите внимание на черный корпус, видимый под ( a ) и ( c ), но не ( b ), что предварительно указывает на более эффективную цилиндрическую набивку для методов набивки с перевернутым конусом и смещения поперечного сечения и вложенных цилиндров.
Второй новый метод складывания называется методом вложенных цилиндров и направлен на полное устранение лишних клапанов за счет использования непрерывных складок. Устройство для способа складывания вложенных цилиндров состоит из нескольких цилиндров, которые размещаются попеременно сверху и снизу ( и ).Ремень для стягивания (сделанный из гибкого листа полимера, ткани, сплава и т. Д.) Также входит в комплект. Для складывания материал кладется на первый цилиндр. Второй цилиндр большего диаметра опускается вокруг первого цилиндра, вдавливая складку в материал. Последовательные цилиндры вводятся одинаковым образом в разных направлениях до тех пор, пока подушка безопасности не будет полностью закрыта. Стягивающий ремень затем помещается вокруг самого внешнего цилиндра и натягивается по мере удаления каждого цилиндра от большого к маленькому.b дополнительно показывает, как складки создаются при добавлении цилиндров, и этот метод дает наиболее точную аппроксимацию исходной модели изогнутой складки с перевернутым конусом по сравнению с другими методами.
Механизм вложенного цилиндра и последовательность складывания с ( a ) изометрическим видом механизма вложенного цилиндра. Обратите внимание на несколько вложенных цилиндров, которые вставляются в разных направлениях от маленького к большому, создавая по одному слою складки за раз.В ( b ) мы видим в разрезе окончательную конфигурацию складок с высотой H , определяемой высотой внутреннего цилиндра, со складками гор и долин, наложенными на подушку безопасности. Затем вокруг внешнего цилиндра помещается стяжной ремень, который натягивается по мере удаления каждого последующего цилиндра от большого к маленькому. Этот метод равномерно распределяет все оставшиеся закрылки.
Этот метод также легко автоматизировать, и он позволяет использовать механизмы с меньшим количеством степеней свободы, чем метод смещения крестовины.Проблемой, связанной с этим методом, является трение между краями цилиндра и тканью, но его можно уменьшить с помощью улучшенной обработки поверхности и размещения роликов по краю цилиндра. Подушка безопасности, сложенная с наложенной на нее складкой в виде перевернутого конуса, показана в c вместе со сравнением базовой линии в b , демонстрируя аналогичные улучшения по сравнению с предыдущими схемами при упаковке в цилиндрический корпус.
3.4. Эффективность развертывания новых методов упаковки
Подушки безопасностибыли развернуты в Университете Бригама Янга для тестирования методов складывания, описанных выше, с полученными изображениями, показанными на.Для оригинального механизма ползунка также были протестированы три вида обработки клапанов: увеличение с четырех до восьми спиц (что привело к уменьшению клапанов), клапаны, сложенные по часовой стрелке и против часовой стрелки, и клапаны, сложенные по карте (складки переворачиваются вместо того, чтобы быть обернутыми в одном направлении). . Развертывания снимались со скоростью 60 кадров в секунду на испытательном стенде, который использует сжатый воздух для надувания подушки безопасности (в результате срабатывание происходит примерно на одной пятнадцатой скорости реальных надувных устройств надувных подушек безопасности). Из-за различий в методах развертывания потребуются дальнейшие тесты развертывания в реальном времени с использованием стандартного тестового оборудования и скорости развертывания, чтобы напрямую сравнить эти результаты с результатами, полученными в сотрудничестве с Autoliv и показанными в.Чтобы определить, выполнялась ли складка в виде перевернутого конуса одинаково в обоих тестах (и, таким образом, если тесты, вероятно, покажут одинаковую производительность), была развернута подушка безопасности, сложенная с использованием того же метода и схемы, и включена, помеченная как «механизм ползунка». В обоих случаях было замечено, что угловое вращение центральной панели между временем 1 (8 мс и 1,48 с соответственно) и временем 3 (22,25 мс и 3,42 с, соответственно) было одинаковым (хотя и в противоположном направлении, вероятно, из-за оставшиеся закрылки завернуты в противоположном направлении), указывая на то, что испытания сжатым воздухом должны показать аналогичные характеристики раскрытия.Каждое развертывание оценивалось на предмет вращательного вращения, и был сделан вывод, что все различные методы складывания закрылков, а также два метода складывания подушек безопасности, описанные ранее (перекрестное смещение и вложенный цилиндр), уменьшали вращение при раскрытии. Чтобы сравнить вращение подушек безопасности, на каждую фотографию были добавлены центральные линии, где видна центральная панель, чтобы сделать сравнение вращений более удобным.
Изображения трех методов упаковки для перевернутого конуса, реализованных в подушках безопасности при испытаниях развертывания на испытательном стенде.Все развертывания производились с использованием сжатого воздуха и были примерно в пятнадцатую часть скорости предыдущих тестов развертывания. Методы упаковки включают в себя механизм ползунка (с использованием четырех механизмов скольжения, тот же метод и узор, показанные ранее под заголовком «перевернутый конус») в качестве базовой линии, а также метод складывания крест-накрест и метод вложенных цилиндров. Осевые линии наложены, чтобы показать ориентацию центральной панели. Столбцы представляют разные способы упаковки, как указано на этикетке. Строки представляют три разных момента времени: 1–1.48 с; 2–1,85 с; 3–3,42 с. Образы были сделаны в те моменты, когда можно было сравнивать важные характеристики развертывания, и на протяжении всего развертывания они примерно такие же, как и предыдущие образы. Метод складывания крестовины и метод вложенного цилиндра, по-видимому, показывают меньшее вращение при развертывании.
Изучая результаты, представленные в, мы видим, что в момент времени 1 (1,48 с) ползунковый механизм (S1) все еще открывается и вращается по часовой стрелке, в то время как складывающийся крест и вложенный цилиндр (FC1 и NC1, соответственно) более устойчивы и далее через развертывание.Во время 2 (1,85 с) все три почти полностью развернуты в радиальном направлении, и мы можем видеть, что центральная панель (прямоугольник) FC2 и NC2 все еще совмещена с их предыдущей фотографией развертывания и более стабильна, чем S2. Наконец, в момент времени 3 (3,42 с) мы видим, что все они полностью развернуты и стабильны. Как метод складывания крестовины, так и метод вложенного цилиндра демонстрируют почти нулевое вращение во время развертывания (что видно по расположению центральной панели, а также по четкости фотографий, указывающих на небольшое движение), в то время как механизм ползунка (складка под названием «перевернутый конус» fold ‘, обсуждавшаяся ранее в § 3), демонстрирует значительное (более 30 °) вращение.
4. Обсуждение и заключение
В этой статье были представлены и оценены схемы складывания и методы упаковки для эффективной упаковки материалов из мягких листов в цилиндрические упакованные формы с настраиваемой высотой и диаметром в сложенном (упакованном) виде, развернутой (развернутой) формой и развернутый размер. Также были изучены производительность развертывания и влияние метода упаковки на развертывание. Двойные шаблоны (мигалка и складка в виде перевернутого конуса) и в общей сложности два метода упаковки для первого шаблона и четыре для второго шаблона были представлены как жизнеспособные решения.Было изучено применение для автомобильных подушек безопасности, и результаты оказались многообещающими, хотя было показано, что мигалка не идеальна для боковых подушек безопасности водителя и, вероятно, будет более полезной в других приложениях Soft Origami.
Оба шаблона складывания имеют регулируемую высоту и диаметр в сложенном состоянии, форму и размер в развернутом состоянии при складывании в приблизительно цилиндрическую форму. Мы смогли повлиять на поведение подушки безопасности, используя этот подход, и предварительные испытания показали, что мы смогли определить поведение в упаковке, поведение при раскладывании посредством раскрытия разности давлений и окончательной развернутой формы.Обе модели показали благоприятные улучшения в упаковке подушки безопасности в цилиндрическую форму с достаточным пространством под упакованным материалом для надувного устройства.
Было создано и исследовано несколько возможных методов складывания перевернутого конуса и шаблонов складывания мигалки с использованием жесткого каркаса, который позже удаляется. После снятия рамы складки готовы к развертыванию за счет перепада давления. Шаблоны, показанные в приложении для складывания автомобильных подушек безопасности, достигли желаемых целей исследования.Продемонстрированные здесь методы упаковки работают при ручном складывании (с комбинацией механизма и вмешательства человека), но еще не автоматизированы, что может стать темой для дальнейшей работы.
Еще одним достижением этого исследования была модификация метода упаковки, основанная на характеристиках развертывания. Хотя использовался один и тот же шаблон (складка в виде перевернутого конуса), было показано, что разные методы упаковки влияют на производительность развертывания, что, вероятно, верно для многих шаблонов и приложений Soft Origami.То есть, в отличие от традиционного оригами, где линии сгиба ограничивают поведение, мягкое оригами допускает более количественный подход, при котором один и тот же узор может быть упакован с использованием множества различных методов (с различной точностью до исходного узора) в зависимости от ограничений приложения. Однако различные методы упаковки и уровни дискретизации приводят к получению упакованных шаблонов, которые соответствуют исходному желаемому шаблону с различной степенью точности.
В заключение были представлены несколько шаблонов и методов упаковки, которые хорошо подходят для упаковки мягкого листового материала в цилиндрический объем перед развертыванием посредством внутреннего давления.Еще одна уникальная разработка в этой работе — использование складной рамы в стиле оригами для наложения рисунка на мягкие листовые материалы, а затем удаление складной рамы и сохранение сложенной формы для использования при развертывании за счет разницы давлений (например, надувание ). Это выгодно для механизма или конструкции, которые представляли бы угрозу безопасности для людей, если бы они имели жесткую основу при развертывании. В приложении к автомобильным подушкам безопасности мы также продемонстрировали принцип изменения метода упаковки (в рамках того же шаблона складывания оригами) в зависимости от характеристик развертывания и требований.
Благодарности
Авторы выражают признательность Брайсу Хансену за помощь с бумажной графикой. Мы выражаем признательность Куину Содерквисту, техническим специалистам и сотрудникам Autoliv, которые проводили тесты развертывания, анализ и технические отзывы по черновикам.
Этика
Это исследование проводилось в соответствии со стандартными университетскими протоколами.
Доступность данных
Все данные, использованные в данном исследовании, представлены на рисунках и в таблице.
Авторские работы
J.Т. выполнил большую часть исследований и написал большую часть черновика рукописи; T.G.N. выполнил основную часть оригинальных исследований в отношении шаблонов складок и начальных методов производства; T.K.Z. выполнил основную часть первоначального исследования структуры складок и начальных методов производства, а также провел дальнейшие исследования, обсуждаемые с целью найти два лучших метода упаковки, и написал часть рукописи; J.D.F. также выполнили обсуждаемые дальнейшие исследования, чтобы найти два лучших метода упаковки; С.ВЕЧЕРА. и L.L.H. критически прочла рукопись и внесла свой вклад в выбор и разработку метода упаковки и схемы сгиба, а также в налаживание сотрудничества с Autoliv. Все авторы обсуждали и комментировали рукопись на всех этапах. Все авторы одобрили окончательную версию для публикации.
Конкурирующие интересы
У нас нет конкурирующих интересов.
Финансирование
Все авторы подтверждают, что этот материал основан на работе, поддержанной Национальным научным фондом и Управлением научных исследований ВВС США, грант NSF No.EFRI-ODISSEI-1240417 и Программа стипендий для аспирантов Национального научного фонда в рамках гранта № 1247046 (T.G.N.). Натуральная поддержка в виде поставок подушек безопасности и средств тестирования, а также поддержка была предоставлена Autoliv.
Ссылки
2. Эдмондсон Б.Дж., Ланг Р.Дж., Хауэлл Л.Л. 2014 г. Техника офсетного панно для толстого жестко складываемого оригами. В Proc. ASME 2014 Int. Конструкторско-техническая техническая конф. И «Компьютеры и информация в инженерии», Буффало, штат Нью-Йорк, 17–20 августа .Нью-Йорк, штат Нью-Йорк: ASME.
4. Zirbel SA, Lang RJ, Thomson MW, Sigel DA, Walkemeyer PE, Trease BP, Magleby SP, Howell LL. 2013. Учет толщины в развертываемых массивах на основе оригами 1. J. Mech. Des. 135, 111005 (doi: 10.1115 / 1.4025372) [Google Scholar]5. Нельсон Т.Г., Ланг Р.Дж., Маглби С.П., Хауэлл Л.Л. 2015 г. Развертываемые развертываемые конструкции большой кривизны с помощью выступающих пластин. В ASME 2015 Int. Конструкторско-техническая техническая конф. & Компьютеры и информация в инженерной конф., Бостон, Массачусетс, 2–5 августа . Нью-Йорк, штат Нью-Йорк: ASME.
6. Koschitz RD. 2014 г. Вычислительный дизайн с изогнутыми складками: подход Дэвида Хаффмана к складыванию бумаги. Докторская диссертация, Массачусетский технологический институт, Кембридж, Массачусетс, США.
10. Цай Дж, Дэн Х, Чжоу Й, Фэн Дж, Ту Й. 2015 г. Бистабильное поведение цилиндрической конструкции оригами с узором Креслинга. J. Mech. Des. 137, 061406 (DOI: 10.1115 / 1.4030158) [Google Scholar] 11. Цай Дж, Дэн Х, Чжан И, Фэн Дж, Чжоу Ю.2016 г. Складывающееся поведение складной призматической мачты с рисунком креслинг-оригами. J. Mech. Робот. 8, 031004 (doi: 10.1115 / 1.4032098) [Google Scholar] 12. Цай Дж, Чжан Ю, Сюй Ю, Чжоу Ю, Фэн Дж. 2016 г. Складываемость цилиндрических складных конструкций на основе жесткого оригами. J. Mech. Des. 138, 031401 (DOI: 10.1115 / 1.4032194) [Google Scholar]13. Lang RJ. 2009 г. Вычислительное оригами: от машущих птиц до космических телескопов. В 25-й год. Symp. on Computational Geometry (eds J Hershberger, E Fogel), стр.159–162. Нью-Йорк, штат Нью-Йорк: ACM.
15. Морган Дж., Ланг Р.Дж., Маглби С.П., Хауэлл Л.Л. 2015 г. Предварительный процесс создания дизайна, адаптированного к оригами. В ASME 2015 Int. Конструкторско-техническая техническая конф. И «Компьютеры и информация в инженерии», Бостон, Массачусетс, 2–5 августа . Нью-Йорк, штат Нью-Йорк: ASME.
16. Курибаяси К., Цучия К., Ю З., Томус Д., Умемото М., Ито Т., Сасаки М. 2006 г. Самораскрывающиеся стент-графты origami в качестве биомедицинского применения фольги из сплава TiNi с памятью формы, богатого никелем. Mater. Sci. Англ. A 419, 131–137. (DOI: 10.1016 / j.msea.2005.12.016) [Google Scholar] 18. Уилер С.М., Калпеппер М.Л. 2015 г. Мягкое оригами: классификация, ограничение и приведение в действие очень совместимых структур оригами. J. Mech. Робот. 8, 051012 (doi: 10.1115 / 1.4032472) [Google Scholar]23. Cromvik C, Eriksson K. 2006 г. Складывание подушки безопасности на основе математики оригами. In Origami 4 (изд. RJ Lang), стр. 129–139. Бока-Ратон, Флорида: CRC Press.
24. Гаттас Дж. М., Ву В., Ю З.2013. Жесткое оригами на основе миуры: параметризация производных первого уровня и кусочно-геометрических фигур.

 Далее полученная схема вырезается и склеивается по отмеченным полоскам.
Далее полученная схема вырезается и склеивается по отмеченным полоскам.


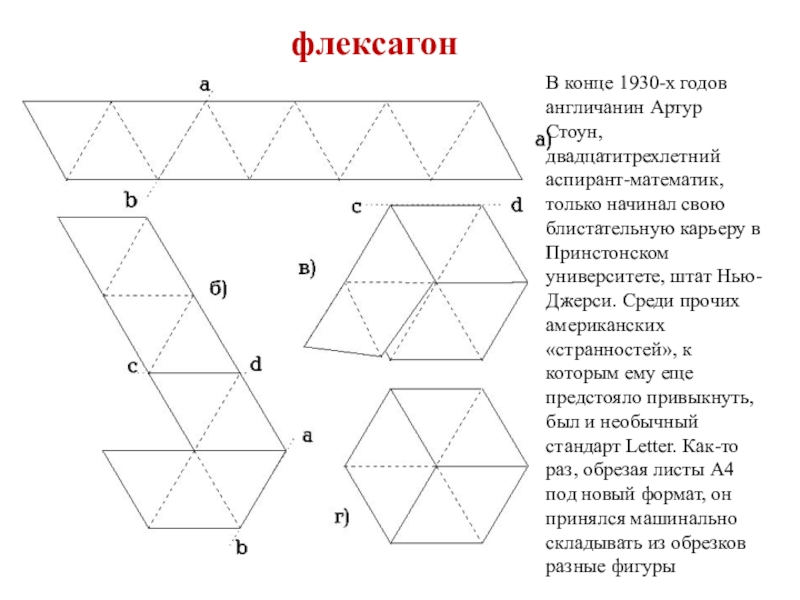

 Н. Задачи по геометрии, решаемые методами складывания (оригами). [Текст]: приложение к журналу «Оригами»./ С. Н. Белим. – Москва: Издательство Аким, 1998
Н. Задачи по геометрии, решаемые методами складывания (оригами). [Текст]: приложение к журналу «Оригами»./ С. Н. Белим. – Москва: Издательство Аким, 1998 html
html Перед тем как приступить к вырезанию предметов, необходимо определиться с их цветовой гаммой.
Перед тем как приступить к вырезанию предметов, необходимо определиться с их цветовой гаммой. Каждая сторона квадрата должна быть примерно 15 см. Ширину треугольника стоит сделать такой же, а высоту 27 см.
Каждая сторона квадрата должна быть примерно 15 см. Ширину треугольника стоит сделать такой же, а высоту 27 см.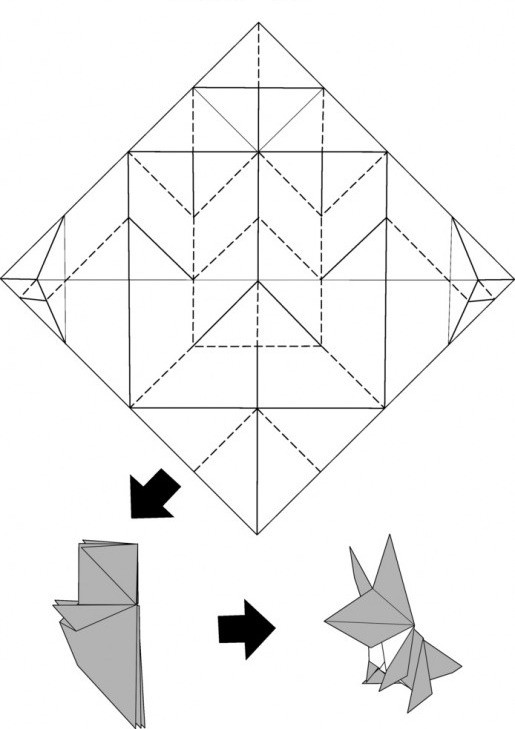 Если фигура создана с каким-либо эзотерическим посылом, то бумажную пирамиду советуется изнутри обклеить фольгой. Это нужно для того чтобы в фигуре накапливалась и не рассеивалась положительная энергия. Если внутрь пирамиды поместить несколько небольших магнитов, то изделие будет обладать магнитной энергией.
Если фигура создана с каким-либо эзотерическим посылом, то бумажную пирамиду советуется изнутри обклеить фольгой. Это нужно для того чтобы в фигуре накапливалась и не рассеивалась положительная энергия. Если внутрь пирамиды поместить несколько небольших магнитов, то изделие будет обладать магнитной энергией. Таким способом можно сделать ровный квадрат.
Таким способом можно сделать ровный квадрат.
 Таким способом можно создать интересный сияющий эффект.
Таким способом можно создать интересный сияющий эффект.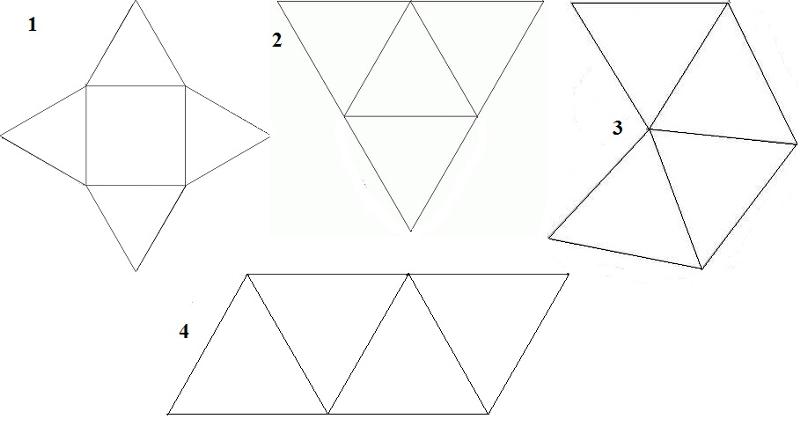
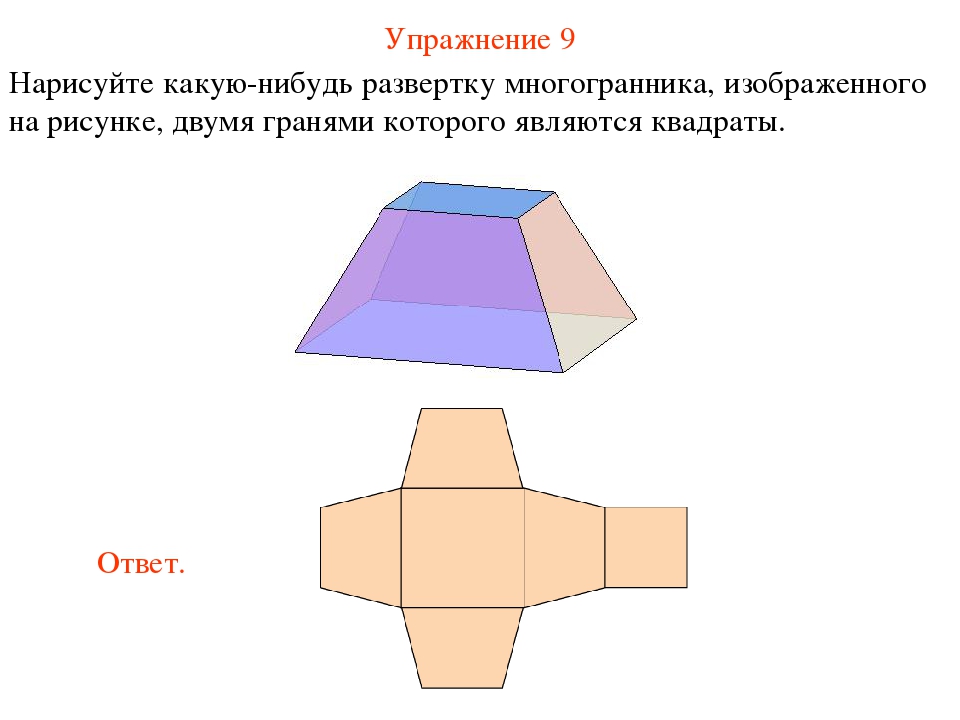 Примером данного стиля есть фигурка журавлика.
Примером данного стиля есть фигурка журавлика. Такую же процедуру проделываем и, с другой стороны.
Такую же процедуру проделываем и, с другой стороны.