Фигурки из треугольников: Поделки из треугольников — фото и картинки: 67 штук

Рисунки из треугольников для детей

Рисование треугольниками

Рисунок из треугольников

Опликацияиз геометрических фигур

Необычные геометрические фигуры

Узор из треугольников

Геометрический рисунок из треугольников

Геометрические фигуры из треугольников

Геометрические Фракталы

Геометрические эскизы

Рисунок из геометрических фигур

Пирамиды Серпинского парадокс

Животные из геометрических фигур

Веселый треугольник

Треугольная аппликация

Фигуры из геометрических фигур

Геометрические фигуры животных для девочки

Мандала Геометрическая

Красивый орнамент из геометрических фигур

«Геометрическая аппликация. Колибри» (вв3351)

Многогранники Эшера

Фигуры из линий

Животные из геометрических фигу

Рисунок из геометрических фигур

Геометрическая абстракция

Фигуры из геометрических фигур

Животные геометрическими фигурами

Треугольные геометрические фигуры для дошкольников

Медведь из треугольников

Красивые рисунки из треугольников

Геометрические животные простые

Треугольная аппликация

Геометрическая аппликация

Аппликация из геометрических фигур

Сложные аппликации из геометрических фигур

Фигуры из геометрических фигур дошкольникам

Оригами рисунок

Аппликация веселая геометрия

Сорва из геометрических фигур

Танграм ящерица

Орнамент виз геометрическихт фигур

Животные геометрическими фигурами

Занятие для малышей треугольник

Орнамент из геометрических фигур

Геометрическая мозаика из треугольников

Квадрат танграм фигуры

Головоломка треугольники

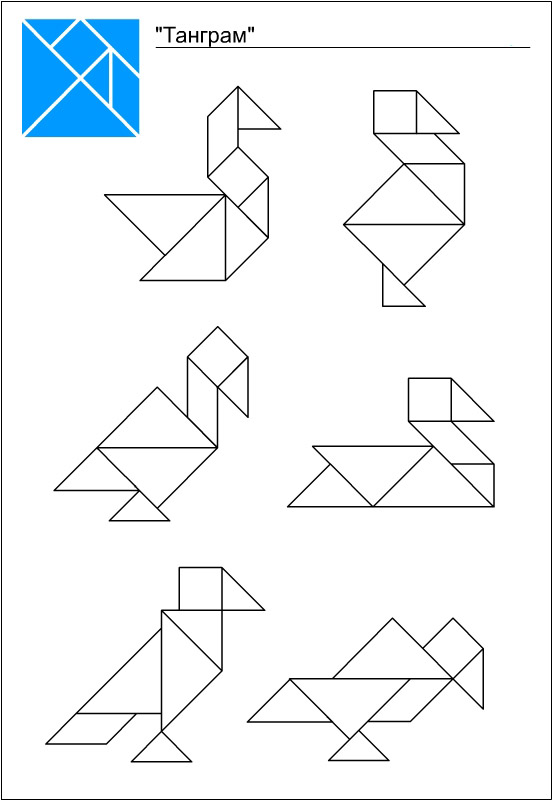
Танграм транспорт схемы для детей

Геометрические фигуры животных

Геометрические животные

Геометрические фигуры для рисования

Рисунок состоящий из треугольников

Геометрические рисунки

Рисование моя семья из геометрических фигур

Стилизованные геометрические фигуры

Выкладывание узора из геометрических фигур

Зверь из геометрических фигур танграм

Геометрические фигуры животных

Необычные геометрические фигуры

Треугольник Серпинского 3d

Аппликация из геометрических фигур

Игра танграм

Звери из геометрических фигур

Диаметрический рисунок

Картины из геометрических фигур

Танграм геометрическое конструирование

Треугольник Серпинского на питоне

Фигурки из линий

Рисование треугольниками

Домик из трёх треугольников

Танграм вертолет

Геометрический Единорог

Комментарии (0)

Написать

Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Фигурное оригами. Модульное оригами схемы

Модульное оригами — это разновидность оригами. Модульное оригами собирается из одинаковых частей (модулей), которые складываются по определённому правилу. Детали при этом между собой не склеиваются, а вставляются одна в другую.

Занимаясь вместе с детьми оригами, вы получаете уникальную возможность развивать у детей внимание, память, усидчивость, пространственное мышление, мелкую моторику рук.

Итак, для того чтобы складывать красивые фигурки оригами например, вот такие как у нас на фото, вам необходимо научиться складывать модули.

Схема сборки модулей.

1. Сложите лист пополам.

2. Наметьте линию сгиба (согните и разогните)

3. Загните углы к центру

4. См. рис.

5. Переверните на другую сторону

6. Свободные концы загните вверх

7. См. рис.

8. Переверните на другую сторону

9. Загните уголки вниз

10. Переверните на другую сторону

11. Отогните края, разогнув уголки

12. Загните края вверх, спрятав уголки вниз

13. Сложите заготовку пополам

14. Модуль готов

Для одной поделки необходимо достаточно большое количество модулей.

Как только вы научитесь их складывать, вы сможете переходить к поиску схем сборки красивых поделок в технике модульного оригами.

Как происходит крепление модулей между собой

Способ 1. Модули на длинных сторонах

Способ 2. Модули на коротких сторонах

Способ 3. Два модуля на длинных сторонах, один — на короткой стороне.

Какой способ сборки модулей следует использовать, будет указано на схеме, которую вы выберете для сборки.

Мы предлагаем вам собрать из модулей Змею — символ 2013 года.

На Новый год можете украсить свой дом новогодними снежинками оригами .

Любители цветов могут попробовать изготовить цветок лотоса. Мастер класс смотрите .

Отличным Пасхальным сувениром и украшением интерьера станет вот такая курочка. Описание изготовления курочки из модулей смотрите .

Из обычных бумажных модулей можно смастерить целый зоопарк.

Мы предлагаем вам смастерить крокодила и черепаху из модулей.

Можно смастерить из бумажных модулей морскую красавицу — рыбку. Мастер-класс по её изготовлению смотрите .

Из бумажных модулей можно собрать даже скорпиона. Как это сделать можно посмотреть .

Из модулей можно сделать стрекозу. Как собрать стрекозу из модулей можно посмотреть

Сегодня во всем мире невероятно популярно любое рукоделие. Сам этот факт парадоксален в условиях ведь все можно купить, но человек испытывает физическую необходимость творить. Это заложено природой и должно находить выход в какой-либо форме. Кроме того, рукоделие очень хорошо действует на нервную систему: работа руками успокаивает человека. Одним из распространенных увлечений взрослых и детей считается оригами, и началом этого процесса является изучение вопроса: «Как сделать из бумаги модуль?»

Что такое оригами

Прежде всего надо сказать, что этот вид декоративно-прикладной деятельности своими корнями уходит в Древний Китай. Именно там впервые начали собирать фигурки из бумаги, а потом это увлечение распространилось на весь мир. Сегодня даже школьники умеют складывать несложные бумажные поделки, а некоторые люди занимаются этим профессионально. В нашей стране составные элементы таких безделушек чаще всего называют кусудама. Кстати, заметим, что оригами из бумаги из модулей — это особый вид работы, который несколько отличается от простой техники. Это направление подразумевает сбор какой-либо фигуры из отдельных частей. Как правило, такие поделки из бумаги, модули для которых могут быть разных цветов и размеров, отличаются сложностью конструкции. Но в самом создании основных элементов нет ничего сложного, и именно об этом мы с вами и поговорим чуть ниже. Но прежде чем разбираться, как сделать из бумаги модуль, надо сказать несколько слов о материалах для поделок.

Бумага

Видов бумаги на канцелярском рынке существует огромное множество, и в принципе, любую можно использовать для создания сувенира. Но для больше всего подходит офисная. Она имеет достаточную плотность, и к тому же поверхность не слишком глянцевая, поэтому с ней удобно работать. Кроме того, для некоторых моделей подходят стикеры разной формы. Также для создания поделок в технике оригами из бумаги (из модулей) можно использовать специальный материал, который так и называется: «Бумага для оригами», а можно купить и обычные разноцветные наборы, предназначенные для детского творчества.

Складывание модулей

Для складывания деталей оригами требуется сноровка и наглядный пример. Как сделать модули из бумаги? Схемы, приведенные на картинке ниже, помогут сориентироваться в этом вопросе. А пока остановимся на ключевых моментах. От размера листочка, выбранного для работы, зависит размер будущего изделия. Обычно берется простой лист А4 и делится на равные кусочки. Чаще всего для модулей используют 1/16 или 1/32 часть. Второй важный момент при рассмотрении вопроса о том, как сделать из бумаги модуль, — это инструменты. Нам понадобятся такие канцелярские принадлежности, как линейка и нож. Бумагу нужно резать аккуратно, чтобы края заготовок были ровными и четкими. Линейка для этих целей выбирается пластиковая или металлическая, которую трудно повредить ножом. Чаще всего для создания оригами клей не нужен, но некоторые модули требуют частичного склеивания. Для этих целей выбирают густой ПВА. Еще могут пригодиться краски и нитки с иглой. Они понадобятся для того, чтобы соединить модули и раскрасить их на свое усмотрение (если бумага белая). С помощью художественной акварели можно добиться красивых переходов одного цвета в другой, а также нанести на части поделки оригинальные узоры.

Приемы складывания

Что же собой представляет модульная сборка оригами? Сразу оговоримся, что здесь существует несколько приемов складывания элементов. К первому из них относится развертка. Это даже не способ, а скорее подготовительный этап к работе. Развертка — это разметка листа бумаги, из которого будет складываться модуль. Вся работа заключается в том, что на лист наносятся линии, по которым будут проходить сгибы. Этот вариант немного сложнее простого складывания оригами по схеме, но в то же время имеет свои плюсы.

Второй способ — мокрое складывание оригами. Эта техника была придумана давно, она позволяет придавать модулям плавные и гибкие формы. Такой метод используют в создании птиц и цветов из бумаги, и, следует заметить, что поделки получаются очень похожими на оригинал. Но для мокрой техники подходит далеко не вся бумага. В данном случае потребуются листы, при изготовлении которых используется клей, а это, как правило, плотные сорта.

Как сложить модуль

Чаще всего в модульном оригами применяются треугольные заготовки. Это самый распространенный вид. Сейчас мы вам расскажем, как сделать из бумаги модуль треугольной формы. Ничего сложного в этом нет. Вам нужно просто следовать следующей инструкции:

1. Сгибаем лист выбранной бумаги пополам.

2. Полученный прямоугольник сложите поперек, чтобы наметилась линия середины.
3. Края модуля загните к середине и переверните.
4. Нижнюю часть заверните вверх.
5. Уголки перегните через получившийся большой треугольник, потом разогните их и нижнюю часть.
6. Теперь опять сложите углы по сгибам и поднимите нижнюю часть вверх.
7. Согните модуль пополам.

В результате должен получиться элемент, два нижних угла которого можно цеплять друг за друга. Из таких модулей можно собрать цветок или птицу, а также вазу или конфетницу. Творите!

В мире рукоделия есть масса идей, реализация которых позволяет сделать простые поделки на Новый год или на другой праздник, чтобы порадовать себя и своих близких. Модульное оригами для начинающих – это очень интересное занятие. Человек может научиться создавать маленькие фигурки из модулей довольно быстро, это легко. В интернете представлены простые схемы, описание которых позволит сделать петуха из бумаги, храм, цветок и т. д.

Модульное оригами для начинающих – это очень интересное занятие

Пошаговая инструкция:

1. Есть вариант приобретения в магазине канцелярии отдельной бумаги для модульного оригами. Но для сборки петуха сгодиться и обычная цветная бумага, правда, она тоньше. Рекомендуется использовать жёлтый материал.
2. Квадратный лист бумаги сгибается пополам. Полученная боковая полоска должна быть согнутой и срезанной по линии сгиба.
3. Затем бумага складывается пополам, образуя прямоугольник.
4. Важно проследить за тем, чтобы верхний и нижний край совпали. Линию сгиба следует прогладить.
5. После этого лист разворачивается. Квадрат складывается повторно, только на этот раз с другой стороны.
6. Бумага складывается вертикально, то есть слева направо.
7. После того, как будет сделана складка, листик разворачивается. Если всё было сделано правильно, то в центре листа должен быть крест.
8. Правый верхний угол прикладывается к нижнему левому углу. Затем делается складка. Действие повторяется, но только с другой стороны.
9. Правая нижняя сторона бумаги со складкой сгибается к центру. Полученный квадрат складывается в ромб. В этом способе не должно получаться треугольных форм листа. Если были образованы фигуры треугольников – это значит то, что рукодел неправильно следовал плану.
10. Углы фигуры нужно собирать к середине. Верхний угол подгоняется к себе. Далее делается складка. Три другие складки отгибаются.
11. Верхний угол квадрата поднимается по линии сгиба вверх. Две другие складки загибаются внутрь.
12. Верхние края листа сворачиваются внутрь. Нужно их расправить.
13. Внешние края получившегося алмаза складываются в центре. Правая складка сгибается к левой.

На последнем этапе фигура переворачивается, и верхний угол нижнего слоя складывается к верхнему углу.

Галерея: модульное оригами (25 фото)

Модульное оригами для начинающих: лебедь (видео)

Елочка при помощи модульного оригами: пошаговая инструкция

Такое объёмное творение, как бумажная елочка, может украсить картины, стенды или деревянные декоративные доски.

Итак, подробная техника:

1. Елка должна быть сделана из зелёной бумаги. Можно использовать как цветную, так и обычную бумагу. Если выбор пал на обычную, то следует воспользоваться красками, чтобы материал приобрёл зелёный оттенок.
2. Собирать ёлочку следует из квадратного листа. Линии сгиба делаются по высоте, ширине и по диагоналям. Бумага разворачивается.
3. Затем складывается базовая модель фигуры – треугольник. Намечается линия сгиба в фигуре. Правая сторона отворачивается к ней.
4. Далее следует использовать линию сгиба, чтобы правый угол фигуры оказался по центру основания треугольника.
5. Все углы заворачиваются.
6. Затем необходимо использовать ножницы, чтобы ёлочка потом стала объёмной. Следует сделать по три надреза с правой и с левой стороны.

Такое объёмное творение, как бумажная елочка, может украсить картины, стенды или деревянные декоративные доски

На последнем этапе полученные отрезки выгибаются в стороны.

Маленькая фигурка человека: простое описание и схема

Для каждой детали человечка можно использовать бумагу разных цветов, например, верх сделать жёлтым, а штаны – синим . Но для упрощения задачи лучше использовать одноцветный материал. Карандашница для создания человечка не нужна.

1. Итак, квадратный материал сгибается пополам, затем сгибаются боковые углы фигуры.
2. В нижней части листа должна быть сделана складка-молния. В верхней части опускается угол. Затем фигура переворачивается.
3. Угол слегка сгибается. Не нужно сгибать его слишком сильно, достаточно слегка наметить линию сгиба.
4. После этого нужно аккуратно расплющить «карманы» получившейся фигуры, сгибая получившийся треугольник.
5. Одна половина изделия сгибается назад.
6. Угол тянется вверх, часть бумаги вытягивается. Вытянутая фигура – это почти готовый человечек.
7. После вытягивания фигуры вверх, должен остаться виден только «нос» треугольника.
8. Угол вгибается внутрь, а голова человечка приподнимается вверх.
9. Остальные верхние углы загибаются внутрь с каждой стороны.

Для каждой детали человечка можно использовать бумагу разных цветов

В конце руки и голову человечка следует приклеить к туловищу.

Советы для тех, кто занимается модульным оригами

• Соединив ниткой несколько оригами, можно украсить этим комнату. Идей масса! Например, можно подвесить поделку на гвоздь у двери. Смотрится очень красиво, особенно, если оригами разноцветные.
• Новичок, желающий совершенствовать свой навык, может поэкспериментировать с разными материалами и цветами.
• Продевать оригами через нить нужно очень аккуратно, чтобы не повредить бумагу.
• В такой работе рекомендуется использовать тонкую бумагу, предназначенную специально для модульного оригами. Почему? Она более тонкая, с ней легко работать. Хотя люди, которые очень интенсивно складывают бумагу, могут порвать её, но если всё делать аккуратно, то поделка получается очень красивой.
• Оригами – это отличный подарок. К новому году можно сделать ёлочку, а к 23 февраля – танк.
• Есть альтернативный материал для создания модульных оригами – это фольга. Из неё поделки получаются более прочные, к тому же они блестящие.
• Чтобы следовать экологическому плану сохранения окружающей среды, можно использовать не новую, а переработанную бумагу.
• Если человек планирует подарить оригами, то последний шаг его завершения рекомендуется делать не заранее, а перед вручением. Так поделка не будет смотреться «помятой».

Соединив ниткой несколько оригами, можно украсить этим комнату

Для создания красивой поделки главное – сделать ровные края. Именно поэтому не рекомендуется использовать материал плохого качества. Если лист надорванный, то элегантное оригами сделать не выйдет.

Как сделать модульное оригами в форме сердечка?

1. Берётся лист бумаги квадратной формы. Цветная сторона повёрнута лицом. Левый верхний угол сгибается к центру. Края должны ровно приложиться друг к другу.
2. Действие повторяется с другим углом. В итоге на материале должно получиться несколько линий сгибов. Разворачивать листик после этого не нужно.
3. Нижняя часть материала сворачивается к центру.
4. Затем листик полностью распрямляется и переворачивается на другую сторону. Если до этого всё было сделано правильно, то в центре листа должна образоваться выпуклость.
5. Далее делается горизонтальный сгиб.
6. Лист повторно переворачивается.
7. Два края бумаги сгибаются к центру. Края фигуры должны соприкоснуться.

Такой подарок очень романтичен

Что нужно подготовить для работы?

• Бумага. Для модульного оригами продаётся специфическая тонкая бумага. Но если такой не нашлось, то можно использовать обычный материал. Главное, чтобы он был квадратной формы.
• Плоская поверхность. Работать удобно на плоской поверхности, на которой бумага будет ровно лежать.
• Линейка. Используется линейка для придания сгибам ровного вида. Однако не обязательно её использовать.

Клубника из бумаги для начинающих (видео)

Если правильно следовать инструкциям, то можно сделать красивейшие модульные оригами своими руками. Главное – иметь желание, и тогда можно будет создать даже самые сложные бумажные изделия.

Для тех, кто всерьез решил постичь древнее японское искусство оригами, я предлагаю начать с простых фигурок. В этой технике совершенно не используется клей. И это очень облегчает работу с бумагой, давая возможность создавать красивые и аккуратные изделия. Модульная же техника этого искусства позволяет придать фигурам объем и интересную фактуру. Давайте посмотрим, как делать модульное оригами.

Оригами из модулей для начинающих

Наше знакомство начнется с изготовления заготовок для модулей. Модули — это бумага, сложенная в виде треугольников. Для этого имеется своя техника сложения бумаги:

Сперва мы берем листы А4 формата, ножницы, линейку и карандаш. Аккуратно размечаем на листе заготовки. На одном листе помещается ровно 16 прямоугольников-основ с размерами 5,3х7,4 см.

После того, как все заготовки разрезаны, начинаем делать модули. Старайтесь выполнять работу максимально аккуратно, ведь каждый модуль — это как пазл в мозаике, он должен быть ровным, чтобы остальные детали смогли незаметно соединиться с ним.

Создавая поделки оригами из модулей для начинающих: схемы очень пригодятся для того, чтобы не запутаться в последовательности соединения элементов.

Тюльпан

На первых парах попробуйте свои силы в сборке простого тюльпана по схеме:

На этой схеме видно, что начинать работу следует с 15 уголков желтого цвета.

Всего цветок должен состоять из 7 рядов, замкнутых в круг.

Также видно, что после 3х рядов идет разделение заготовки на 3 клина — будущие лепестки цветка.

В итоге у нас должен получиться вот такой цветок:

Подробнее смотрите на видео:

Оригами из модулей для начинающих Змея

Отточить навыки соединения деталей можно при сборке простой модели змеи. Схема этой фигуры очень простая:

А в результате у нас получится вот такая безобидная яркая змейка:

Всего для работы нам потребуется 121 модуль. Начинать следует с головы фигуры:

Следуя указаниям схемы мы увеличиваем тело змеи в 5 ряду до 5 модулей.

И делаем глазки змеи.

Все остальные действия выполняем строго придерживаясь схемы:

В местах изгибов фигуры уделяем особое внимание присоединению модулей следующего ряда:

Продолжаем соединение деталей до тех пор, пока не дойдем до хвоста змеи:

Заключительным штрихом в работе будет приклеивание языка:

Обязательно посмотрите предложенные ниже видео уроки.

Долька арбуза

Еще одной простой схемой оригами из треугольных модулей для начинающих обладает аппетитная арбузная долька:

В этой фигуре нет ничего сложного, и она отлично подойдет для занятий детским творчеством.

В общей сложности нам потребуется 213 модулей разных цветов: 114 красных, 66 зеленых, 17 белых и 16 черных треугольников.

Начинаем создавать нашу дольку с кожуры зеленого цвета. В первом ряду у нас будет 15 зеленых модулей. Их нужно расположить коротким основанием треугольника вверх.

Потом во втором ряду мы добавляем 14 зеленых элементов, но теперь уже длинная сторона должна оказаться наверху.

Третий ряд кожуры снова состоит из 15 модулей. В четвертом ряду снова убавляем количество на 1 = 14 элементов.

Начиная с 5го ряда, мы начинаем добавлять новые цвета. Во-первых, делаем белую прослойку между кожурой и мякотью арбуза. Располагаем модули по схеме: 2 зеленых, 13 белых и снова 2 зеленых.

Теперь мы перешли к самой мякоти будущее спелого арбуза. В 6м ряду у нас будет 3 цвета. Располагаем модули в следующей последовательности: 1 зеленый, 1 белый, 12 красных, 1 белый и опять 1 зеленый.

7 ряд будет состоять из 15 модулей: 1 белый, 13 красных, снова 1 белый.

В 8м ряду начинаем добавлять арбузные косточки. Располагаем модули по очереди, начиная и заканчивая ряд красными элементами. Всего будет 14 модулей.

Чтобы придать арбузной дольке треугольную форму, в последующих рядах мы будем сокращать количество модулей.

Весь девятый ряд будет состоять только из 13 красных элементов.

В 10 и 12 рядах снова располагаем треугольники в последовательности красный-черный, аналогично 8 ряду.

В 11 ряду у нас будут только красные модули. А с 13 по 21 ряды уменьшаем количество элементов на 1. Все модули у нас будут красными.

В 21м ряду у нас должен остаться 1 треугольник.

Для тех, кто хочет наглядно понять, как делать оригами из модулей для начинающих, видео также прилагаю:

Наша арбузная долька готова. Выглядит она очень аппетитно:

Старайтесь использовать в своей работе бумагу ярких, насыщенных цветов. Она поможет придать вашим фигурам еще большую реалистичность.

Теперь вы знаете, как сделать модульное оригами для начинающих, а этот кусочек арбуза станет по истине лакомым.

Модульное оригами – это особый вид искусства создания фигурок из бумаги. Как правило, это объёмные фигуры из одинаковых частей (например, огромные шары, звезды). Элементы изделия держатся друг с другом за счёт вкладывания. Объёмные шары носят название “кусудама”.

Особенности

На первый взгляд эта техника существенно отличается классической. Среди её особенностей следующие:

• модулями большой фигуры чаще всего бывают треугольные модели
• при правильной сборке, а именно вкладывании фигур друг в друга, можно разобрать изделие и создать что-то новое
• сборка осуществляется по длинной стороне, короткой или по обеим сторонам

Самая простое творение состоит из 20 заготовок.

Выбор материала

Рекомендуем использовать цветную бумагу. На белом листе очень заметны огрехи, потёртости или примятости – это может испортить настроение и надолго отвадить от творчества. Также в помощь новичкам понадобятся ножницы и клей ПВА. Конечно, разобрать склеенную творение невозможно, но зато оно не будет разваливаться в руках.

Польза для начинающих

Новички (будь то дети или взрослые) с помощью этой техники развивают ряд навыков. Например:

• усидчивость
• скурпулёзность
• мелкую моторику
• пространственное мышление
• тренируют внимание и аналитическое мышление

Советуем для начала сделать в этой технике простые фигурки. На них проще понять принцип сборки воедино. Принцип этой техники настолько прост, что данным видом моделирования занимаются дети в школьных садах и младшие школьники.

Создание модуля

Прежде всего нужно научиться делать составные заготовки. Самыми простыми из них являются треугольники.

Изготовьте их, выполняя следующие действия:

1. Приготовьте небольшие прямоугольные листики бумаги. Из формата А4 вырезают 16 или 32 прямоугольника. Лучше выбрать листики более крупного формата.
2. Сложите прямоугольник вдоль. Тщательно продавливайте линии.
3. Согните края к середине. Заготовка должна напоминать бумажный самолёт.
4. Переверните другой стороной к себе.
5. Внизу видно 2 маленьких прямоугольника. Их нужно загнуть вверх.
6. Теперь загибаем верхние углы (соответственно левый верхний для левого и верхний правый для правого) прямоугольника за большой треугольник. Таким образом «цепляем» за края.
7. Обратно отгибаем. С загнутыми уголками (как уголок книги), поднимите края вверх.
8. Получившийся треугольник согнуть пополам.

У заготовки должно получиться 2 уголка и 2 кармашка. Типы вкладывания уже были упомянуты в этой статье.

Принципы создания описывают схемами. Для начала в помощь будут видео- и фотоматериалы, которых очень много на интернет-просторах. Существует много подробных пошаговых фото-инструкций по созданию.

Цыплёнок в мастер классе

Это одна из самых простых фигурок для исполнения. Для её сборки нужно 40 жёлтых мод., и 5 красных. Схема сборки: модули вкладываются друг в друга длинной стороной.
Вот такой цыплёнок у вас должен получиться!

9-ый: 2 модуля красного цвета (ножки)

Посередине первого ряда делаем гребешок из 3 мод. , красного цвета. Дополнительно из бумаги вырезаем глаза и клюв. Это изделие двухмерное. Для создания объёмных деталей нужно располагать детали по кругу, делая определённую «кладку». Одной схемой можно воспользоваться несколько раз и меняя цвета, добавляя (убирая) детали, получить попугая или пингвина.

Треугольники в геометрии — определение, форма, типы, свойства

Что такое треугольники?

Треугольник — это замкнутая двумерная фигура с 3 сторонами, 3 углами и 3 вершинами. Треугольник также является многоугольником.

На приведенном выше рисунке изображен треугольник, обозначенный буквой △ABC.

Родственные игры

Примеры треугольников

Некоторые примеры треугольников из реальной жизни включают бутерброды, дорожные знаки, вешалки для одежды и стойку для бильярда.

Связанные рабочие листы

Непримеры треугольников

Приведенные выше цифры не являются примерами треугольников. Эти фигуры нельзя назвать треугольниками, так как –

• Первая фигура четырехсторонняя.
• Вторая фигура представляет собой открытую форму.
• Третья фигурка имеет изогнутую сторону.

Части треугольника

1. Треугольник имеет 3 стороны. В треугольнике АВС стороны равны АВ, ВС и СА.
2. Угол, образованный любыми двумя сторонами треугольника, является углом треугольника, обозначаемым символом ∠. Треугольник имеет три угла. Три угла треугольника ABC равны ∠ABC, ∠BCA и ∠CAB. Эти углы также называются ∠B, ∠C и ∠A соответственно.
3. Точка пересечения любых двух сторон треугольника называется вершиной. Треугольник имеет три вершины. В треугольнике ABC вершинами являются A, B и C.

Свойства треугольника

• Сумма всех трех внутренних углов треугольника всегда равна 180⁰.
• Сумма длин любых двух сторон треугольника всегда больше длины третьей стороны.
• Площадь треугольника равна половине произведения его основания на высоту.

Типы треугольников

Треугольники можно классифицировать на основе длины сторон или измерения их углов.

Чтобы классифицировать треугольники по их углам, мы измеряем каждый из их внутренних углов. Треугольники можно классифицировать по углам, как:

• Остроугольный треугольник или остроугольный треугольник
• Прямоугольный треугольник или прямоугольный треугольник
• Тупоугольный треугольник или тупоугольный треугольник

Типы треугольников в зависимости от длины сторон –

• Разносторонний треугольник
• Равнобедренный треугольник
• Равносторонний треугольник

Чтобы классифицировать треугольники по углам и сторонам, мы измеряем внутренние углы и длину сторон треугольника. Треугольники, классифицируемые как по углам, так и по сторонам: –

• Остроугольный равносторонний треугольник
• Прямоугольный равнобедренный треугольник
• Тупоугольный разносторонний треугольник

Площадь треугольника

Площадь треугольника — это область, которую треугольник занимает в двумерном пространстве. Площадь разных треугольников различается в зависимости от их размера. Зная длину основания и высоту треугольника, мы можем определить его площадь. Выражается в квадратных единицах.

Итак, площадь треугольника = ½ (произведение основания и высоты треугольника)

В треугольнике PQR стороны PQ, QR и RP. QR — основание треугольника, а PS — высота треугольника. PS перпендикулярен из вершины P к стороне QR. Итак, чтобы найти площадь △PQR, мы используем следующую формулу:

Площадь △PQR = ½ (произведение основания и высоты треугольника)

Или площадь △PQR = ½ (QR X PS)

Периметр треугольника

Периметр треугольника равен сумме длин всех сторон треугольника.

Итак, периметр треугольника = сумма всех трех сторон.

В треугольнике PQR периметр будет суммой трех сторон, то есть PQ, QR и RP.

Итак, периметр △PQR = PQ + QR + RP.

Решенные примеры на треугольнике

В. Найдите площадь треугольника с основанием 10 см и высотой 8 см.

Ответ. Для данного треугольника основание = 10 см и высота = 8 см

Мы знаем, что

Площадь треугольника = ½ (Произведение основания и высоты треугольника)

Итак, площадь данного треугольника = ½ (10 x 8) = ½ (80) = 40 см ²

В. Используя рисунок ниже, найдите периметр треугольника ABC.

Ответ. Мы знаем, что Периметр треугольника = (Сумма всех сторон треугольника)

На данном рисунке длины сторон треугольника ABC равны

AB= 5 см, CA= 5 см и BC= 7 см. .

Итак, периметр △ABC= AB + BC + CA = 5 + 7 + 5 = 17 см.

В. Определите, является ли данная фигура треугольником, а также объясните причины.

Б.

В.

Ответ. А. Данная фигура является треугольником, так как имеет три прямые стороны и является замкнутой фигурой.

B. Форма не является треугольником, так как имеет четыре стороны.

C. Форма не является треугольником, так как это открытая фигура с тремя открытыми сторонами.

Q. Периметр треугольника PQR равен 16 см, а стороны PQ и QR равны 4 см и 6 см. Найдите длину третьей стороны треугольника.

Ответ. Мы знаем, что периметр треугольника = (сумма всех сторон треугольника)

Итак, периметр △PQR= PQ + QR + RP

16 = 4 + 6 + RP

RP= 16 – 10 = 6см

Итак, длина третьей стороны 6см.

Q. Углы A и B треугольника ABC равны 70⁰ и 60⁰ соответственно. Найдите третий угол C.

Ответ. Мы знаем, что сумма всех углов треугольника равна 180⁰.

Итак, ∠A + ∠B + ∠C = 180⁰

70⁰ + 60⁰ + ∠C = 180⁰

∠C = 180⁰ – 130⁰ = 50⁰ 900 05

Третий угол треугольника равен 50⁰.

В. Можно ли составить треугольник со сторонами 2 см, 3 см и 6 см?

Ответ. Чтобы образовался треугольник, сумма любых двух сторон всегда должна быть больше третьей стороны.

Для данных размеров 3 см + 6 см = 9 см больше 2 см, 6 см + 2 см = 8 см больше 3 см, но 2 см + 3 см = 5 см меньше 6 см. Таким образом, данные меры не могут образовывать треугольник.

В. Если площадь треугольника 20 см, а длина его основания 5 см, найдите высоту треугольника.

Ответ. Мы знаем, что площадь треугольника = ½ x основание x высота

Итак, 20 = ½ x 5 x высота

Высота треугольника = (20 x 2) / 5 = 8 см

Практические задачи на треугольник

1

Выберите лишнее.

Разносторонний треугольник

Остроугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Правильный ответ: Остроугольный треугольник углы. 9{2}$.

Заключение

Геометрия — важный аспект математики, требующий углубленного изучения. Концепция треугольников является фундаментальной темой в геометрии для маленьких детей. Благодаря интерактивному обучению с помощью подробных материалов курса от SplashLearn ваш ребенок узнает о треугольниках, их типах и свойствах, а также попрактикуется в играх и рабочих листах.

Равнобедренный треугольник — определение, углы, свойства, примеры

Что такое равнобедренный треугольник?

Треугольник с двумя сторонами равной длины является равнобедренным треугольником.

Примеры равнобедренного треугольника:

Неравнобедренный треугольник:

Примеры равнобедренного треугольника в реальной жизни:

Многие вещи в мире имеют форму равнобедренного треугольника. Некоторые популярные примеры этих треугольников в реальной жизни:

Родственные игры

Части равнобедренного треугольника

 Части равнобедренного треугольника

1. Катеты: Две равные стороны равнобедренного треугольника называются катетами. В треугольнике ABC (данном выше) AB и AC являются двумя катетами равнобедренного треугольника.

2. Основание: Основанием равнобедренного треугольника является третья и неравная сторона. В треугольнике АВС основание равнобедренного треугольника ВС.

3. Угол при вершине: «Угол при вершине» — это угол, образованный двумя равными сторонами равнобедренного треугольника. ∠BAC — угол при вершине равнобедренного треугольника.

4. Углы при основании: «Углы при основании» — это углы, которые опираются на основание равнобедренного треугольника. ∠ABC и ∠ACB — два угла при основании равнобедренного треугольника.

Похожие рабочие листы

Свойства равнобедренного треугольника

Вот список некоторых свойств равнобедренных треугольников:

• В равнобедренном треугольнике, если две стороны равны, то углы, противоположные двум сторонам, соответствуют друг другу и также всегда равны.

В приведенном выше равнобедренном треугольнике два угла ∠B и ∠C, лежащие напротив равных сторон AB и AC, равны друг другу.

• Равнобедренный треугольник имеет три острых угла, то есть углы меньше 90°.
• Сумма трех углов равнобедренного треугольника всегда равна 180°.

Типы равнобедренных треугольников

 Как правило, равнобедренные треугольники подразделяются на три различных типа:

• Равнобедренный остроугольный треугольник: Равнобедренный остроугольный треугольник – это треугольник, в котором все три угла меньше 90°, и по крайней мере два его угла равны по измерению. Одним из примеров углов равнобедренного остроугольного треугольника являются 50 °, 50 ° и 80 °.

• Равнобедренный прямоугольный треугольник: Ниже приведен пример прямоугольного треугольника с двумя катетами (и соответствующими им углами) равной величины.

• Равнобедренный тупоугольный треугольник: Равнобедренный тупоугольный треугольник — это треугольник, в котором один из трех углов тупой (лежит между 90° и 180°), а два других острых угла равны по измерению. Один пример углов равнобедренного тупого треугольника составляет 30 °, 30 ° и 120 °.

Площадь и периметр равнобедренного треугольника

• Площадь равнобедренного треугольника находится по следующей формуле:

Площадь (A) = ½ × основание (b) × высота (h)

• Периметр равнобедренного треугольника находится по формуле:

Периметр (P) = 2a + основание (b)

Здесь «a» относится к длине равных сторон равнобедренного треугольника, а «b» относится к длине третьей неравной стороны.

Решенные примеры

Пример 1

Какова высота равнобедренного треугольника с площадью 12 кв.см и основанием 6см?

Решение:

Площадь равнобедренного треугольника = ½ x основание x высота

т.е. 12 = ½ x 6 x высота

т.е. высота = 4 см

Пример 2

Что равен периметру равнобедренного треугольника, если равные стороны равны a см каждая, а неравная сторона равна b см?

Решение:

Периметр равнобедренного треугольника = сумма его сторон

Периметр равнобедренного треугольника = (a + a + b) см, т. е. (2a + b) см

Пример 3

900 04 Найти периметр равнобедренного треугольника, если основание равно 16 см, а равные стороны по 24 см каждая.

Решение: 

Формула периметра равнобедренного треугольника, P = 2a + b

Здесь a (стороны) = 24 см и b (основание) = 16 см

Следовательно, периметр равнобедренного треугольника P = 2(24) + 16 = 64 см.

Следовательно, периметр равен 64 см.

Игры с треугольниками

С SplashLearn есть несколько игр о треугольниках, которые дети могут попробовать. Давайте рассмотрим некоторые из них:

• Определение типов треугольников : В этой игре ваш ребенок будет определять различные типы треугольников. Они будут использовать данные атрибуты, чтобы определить правильный треугольник и изучить характеристики треугольника. Учащиеся выбирают правильный ответ из предложенных.
• Classify Triangles : В игре вашему ребенку предлагается отточить свои навыки, решая ряд задач, связанных с двухмерными фигурами, для определения различных типов треугольников. Учащиеся будут анализировать стороны треугольника и измерения углов и классифицировать каждую из них в соответствующей категории.

Другие игры

• Классифицируй треугольники и прямоугольники как замкнутые фигуры :   Эта игра поможет детям классифицировать различные типы фигур и поможет их запомнить. Это поможет вашему ребенку быстрее и легче распознавать различные формы.
• Сортировка фигур по имени : Это будет веселая игра, в конце которой ваш ребенок узнает все о различных формах! Игра включает в себя сортировку фигур по их именам, и таким образом ваш юный математик получит больше практики с концепциями 2D-форм. Эта игра подтолкнет вашего ребенка к мастерству, развивая при этом общие математические способности.

Ученикам также может быть сложно запомнить свойства равнобедренных треугольников. Но именно здесь вам потребуется много терпения при обучении вашего ребенка. Позвольте вашему ребенку сиять ярко с SplashLearn .

---

Практические задачи на равнобедренные треугольники

1

Какова высота равнобедренного треугольника с площадью 10 кв. см и основанием 5 см?

10 см

5 см

2 см

4 см

Правильный ответ: 4 см
Площадь равнобедренного треугольника = ½ x основание x высота, т. е. 10 см ^{2 9012 4 = ½ х 5 см х высота.. т. е. высота = 4 см}

2

В ΔABC, если ∠A = ∠B, то

AC ≠ BC

AC = BC

AB = AC

AB = BC

Правильный ответ: AC = BC
Стороны, противоположные равным углам, также равны. ∠A = ∠B, BC противоположен ∠A, а AC противоположен углу B. Следовательно, AC = BC в ΔABC.

3

Какова площадь равнобедренного треугольника, указанного ниже?

21 см ²

45 см ²

90 см ²

180 см ²

Правильный ответ: 45 см ²
Площадь Isosceles Triangle = ½ x Base x Height = ½ x 15 см x 6 см = 45 см ²

---

Часто задаваемые вопросы

Как мы знаем, является ли треундль Isosceles?

Треугольник называется равнобедренным, если две его стороны равны. Возьмем треугольник, у которого три стороны АВ, ВС и СА.