Плетение на веточках | Страна Мастеров
Лето — пора отдыха и путешествий. Когда побываешь в прекрасных уголках природы, хочется оставить в памяти удивительные места с прекрасными растениями и могучими деревьями. Можно сплести себе такое памятное дерево на счастье, используя очень древний способ плетения на веточке.
Для начала во время прогулок в лесу нужно подобрать подходящую веточку. Она должна быть гибкой и достаточно ровной, чтобы её можно было свернуть в кольцо. Если плести будете не сразу, то оставьте веточку в мокрой ткани, чтобы она не пересохла. Сворачивать веточку нужно очень медленно, постепенно, чтобы не сломать. Когда кольцо получилось, зафиксируйте ниточкой.
Место соединения веточки обмотайте ниткой плотными рядами и завяжите в конце.
Отмерьте длину нитей для основы. Сложенная вдвое, она должна быть немного больше диаметра кольца. Нарежьте таких ниточек 10—16 штук. (Чётное количество). И ещё одну — в три раза длиннее.
Навесьте ниточки, закрепляя их петлями на ветке, на небольшом расстоянии.
В центре повесьте самую длинную нитку, короткие — по обе стороны.
Соберите в пучок все короткие нитки. Возьмите небольшой кусочек нитки, свяжите пучок и привяжите его к основанию. Нитки сильно не натягивайте.
Сведите все нитки вместе немного ниже центра окружности, перехватите их длинной ниткой и этой же ниткой выполните ствол, плотными рядами оборачивая пучок. У основания этой же ниткой несколько раз крест-накрест закрепите ствол. Мы получили наше дерево. У него уже есть ствол, ветки и корень. Осталось оформить крону.
Отрежьте толстую нитку, закрепите у края первой веточки. Выполняйте плетение между веточками в шахматном порядке.
Вплетать можно не только ниточки, но и ленточки или полоски тканей.
Когда меняете нитку или полоску, начало следующей можно привязать к концу
предыдущей, узелок спрятать на изнанке.
обязательно.
Можно сделать цветущее деревце, смастерив небольшие цветочки из пучков ниток и вставив их между плетением.
А можно украсить деревце листочками, вырезанными из несыпучей ткани.
На летней встрече помощников сайта в Псковской области мы мастерили памятные деревья все вместе. ЛиЛеКа сделала три деревца на разные сезоны. Морозная зима, нежная весна и разноцветное лето.
Темнова Елена, Морошка-Юлия, Sahalin, Ларисочка, Леночка, Татьяна Безрукова и Голубка — каждая мастерица внесла свою особенную изюминку в образ дерева. Японский клён Лены Темновой на ярко-красной траве напоминает о скорой осени. На воздушное и прозрачное деревце Морошки-Юли присел журавлик счастья. Пышная осенняя живопись получилась у Ирины (Sahalin). На осеннее деревце Ларисочки тоже присел журавлик перед отлётом в тёплые края. Но дереву с такими корнями не страшны ветра и холода. А дерево Леночки словно уже познакомилось с первыми морозами — льдинки блестят на стволе, хотя крона полна ещё ярких красок.
Все увезли с собой частичку этого прекрасного места, а также море душевного тепла от радостного общения и совместного творчества.
Ярнбомбинг — не пора ли присоединиться?
Новинки
Каталог товаров
Войти Регистрация
- Главная
- Статьи
- Ярнбомбинг — не пора ли присоединиться?
Стать ярнбомбером проще простого. Если у вас припасены остатки пряжи, которые «когда-нибудь пригодятся», то основа для начала «карьеры» уже есть. Не пора ли разворошить эти запасы? Пусть теперь порадуют глаз и согреют душу окружающим! Для тех, кто еще ни разу не встречал на пути вязаное дерево, небольшая справка: Yarn bombing, в переводе «бомбардировка пряжей» или «взрыв пряжи», «распространение пряжи» – вид уличного искусства, в котором вместо красок используются яркие демонстрации вязания или пряжи.
Первую идею ярнбомбинга придумала одна замечательная американка, творческая натура, Магда Сайег – владелица маленького магазинчика товаров для рукоделия. В ожидании покупателей она просто обвязала яркой пряжей ручку входной двери. Получилось весело и мило.
Фишку мгновенно подхватили фанаты вязания, и на улицах города стали появляться другие подобные шедевры. Из бабушкиного занятия вязание выросло в особый вид сити-арта, который быстро разлетелся по городам и странам.
Вязаные проекты перекочевали на деревья, фонарные столбы, скамейки, а далее достигли глобальных масштабов, вплоть до памятников, автомобилей, домов и целых площадей.
Яркие праздничные цвета на улицах улыбают прохожих и поднимают настроение, разгоняют стрессы, и даже бросают дерзкий вызов обстоятельствам.
С чего начать освоение ярнбомбинга?
Обвязка дерева считается самым простым вариантом этого вида искусства. Даже те, кто только учится вязать, могут начинать прямо сейчас.
Даже те, кто только учится вязать, могут начинать прямо сейчас.
Самая простая манера украшения — это обматывание ствола нитками. Кольца нужно укладывать вплотную друг к другу, иначе декор будет выглядеть непривлекательно и неряшливо. Цветной участок можно дополнительно украсить вязаными элементами, бусинами,пуговицами или другой фурнитурой.
Отлично подойдет для такой цели толстая пряжа, особенно трикотажная пряжа Love Is от Домпряжи. Благодаря толщине нити 7-9 мм можно очень быстро создать шедевр больших размеров, а эластичная нить легко окутает любую форму. Разнообразие расцветок и наличие разноцветных мотков идеально для эффектного результата.
Другой упрощенный вариант ярнбомбинга: обмотать ствол не нитками, а вязаными цепочками или шнурами, подключив фантазию и море идей, чтобы сделать их не скучными.
Ну а если все же решиться на полноценную одежку для ствола, то крючком это сделать проще. Чтобы угадать с размером, первую цепочку можно обернуть вокруг дерева, а далее вязать в высоту с учетом очертаний ствола. Если дерево сужается к верху, то петли нужно будет постепенно сокращать, иначе шкурка будет сползать, как растянутый чулок.
Чтобы угадать с размером, первую цепочку можно обернуть вокруг дерева, а далее вязать в высоту с учетом очертаний ствола. Если дерево сужается к верху, то петли нужно будет постепенно сокращать, иначе шкурка будет сползать, как растянутый чулок.
При вязании спицами нужно сначала рассчитать количество петель. Для упрощения и ускорения задачи можно вязать не вдоль ствола, а поперек. Если дерево в зоне доступа, то поправки удобно делать сразу на месте, прикладывая время от времени вязание к стволу. Если такой возможности нет, то лучше сразу снять мерки с дерева-модели.
Процесс довольно трудоемкий, но оно того стоит. Представьте, вот вы уже любуетесь своей первой творческой работой в стиле ярнбомбинга, оцениваете все ее достоинства и недостатки, осознаете ошибки, и тут же рождаются новые идеи и способы воплощения. Все, процесс, как говорится, пошел!
А что дальше?
А дальше у вас есть мы. Потому что если вы решите разгуляться создать действительно заметный стрит-шедевр, возле которого каждый захочет сделать селфи и разослать по сетям, то вам понадобится энное количество километров пряжи. А мы ее уже приготовили!
Потому что если вы решите разгуляться создать действительно заметный стрит-шедевр, возле которого каждый захочет сделать селфи и разослать по сетям, то вам понадобится энное количество километров пряжи. А мы ее уже приготовили!
Итальянская бобинная пряжа разных видов и разного состава — у нас постоянные поставки восхитительных цветов и фактур. В некоторых марках «итальянки» на 100 граммов веса приходится 1400 метров нити. С таким размахом вы не только захотите переодеть всю улицу, но и сами будете не прочь обновить свой гардероб.
Вязание перестало быть просто увлечением и уже давно «вышло из берегов». Платные услуги по ярнбомбингу теперь не новость. Можно заказать обвязку любого объекта, вплоть до целого дома. А что мешает оформить вязаную вечеринку или даже свадьбу? Творческим людям с неограниченным полетом мысли подвластно все.
Добро пожаловать в Дом Пряжи, ждем!
И да, вполне реально появление в скором времени новой профессии – вязайнер. Ведь связать полотно – не основная часть работы. Нужно еще придумать, как его закрепить, чтобы не повредить объект, позаботиться о том, чтобы пряжа долго не выгорала, не линяла, и многое-многое другое.
Ведь связать полотно – не основная часть работы. Нужно еще придумать, как его закрепить, чтобы не повредить объект, позаботиться о том, чтобы пряжа долго не выгорала, не линяла, и многое-многое другое.
Побусякать эти товары
Москва
Новосибирск
Санкт-Петербург
Глубокое погружение в многопоточное двоичное дерево шаг за шагом | Видип Малхотра | Аналитика Vidhya
Знакомы ли вы с концепциями потокового двоичного дерева и его преимуществами по сравнению со стандартными двоичными деревьями (BT) / двоичным деревом поиска (BST)? Что ж, эта статья даст вам пошаговый анализ Threaded Binary Tree и его реализации. В этой статье я не буду подробно рассказывать о двоичных деревьях и двоичных деревьях поиска, эта статья посвящена пониманию многопоточных двоичных деревьев: их преимуществам перед двоичным деревом и их реализации. Я предполагаю, что вы знакомы с бинарными деревьями и бинарными деревьями поиска.
Я предполагаю, что вы знакомы с бинарными деревьями и бинарными деревьями поиска.
Многопоточные двоичные деревья по названию предполагают, что узлы связаны с потоками, но подождите, узлы связаны THREAD , но почему и как имеет какое-либо значение по сравнению с обычным двоичным деревом поиска. У меня было еще несколько вопросов по Threaded Binary Trees:
Q1. Что такое многопоточное бинарное дерево?
Q2. Чем это лучше, чем бинарное дерево?
Q3. Какие существуют типы многопоточного двоичного дерева?
Q4. Как многопоточное двоичное дерево будет реализовано в Python?
Мы разберем каждый вопрос по очереди. Существует два типа потокового двоичного дерева. Начнем с определения каждого из них:
В Double Threaded Binary Tree левый указатель узла должен указывать на предшественника Inorder , а правый указатель должен указывать на преемника Inorder. Единственным исключением является то, что левый указатель самого левого узла в дереве и правый указатель самого правого узла в дереве должны указывать на НОЛЬ .
В Single Threaded Binary Tree левый или правый указатель узла указывает на предшественника или преемника Inorder. Исключением является то же самое для двухпоточного двоичного дерева, что левый указатель самого левого узла в дереве и правый указатель самого правого узла в дереве должны указывать на NULL .
Запутался? Давайте визуализируем это.
Ниже приведено простое двоичное дерево поиска:
Двоичное дерево поискаТеперь проблема с бинарным деревом/бинарным деревом поиска заключается в том, что левых и правых указателей дочерних узлов тратятся впустую, поскольку все они указывают на нуль , поэтому нам нужно использовать эти указатели для лучшего обхода, но как и почему?
Ответ почему:
В простом итеративном обходе Inorder нам нужно использовать стек для обхода дерева Inorder; таким образом, преобразуя дерево в многопоточное двоичное дерево, нам не нужно использовать стек для обхода Inorder.
Таким образом экономится место.
Второе преимущество заключается в том, что для перехода от дочернего узла к корневому узлу требуется меньше обхода; таким образом, это улучшит функцию поиска в древовидных алгоритмах, которая требует постоянного потока логики для частого перехода вверх и назад по дереву.
Я считаю, что объяснение с реализацией даст лучшее понимание. В этой статье мы будем анализировать двухпоточное дерево.
Ответ на Как:
Я предполагаю, что большинство из вас сразу перейдет к реализации, так что теперь давайте начнем интересную часть: Как это реализовано?
Давайте посмотрим на упорядоченный обход дерева ниже:
Неупорядоченный обход двоичного дерева поискаНеупорядоченный обход дерева выше:
5 -> 7 -> 8 -> 10-> 25 -> 30(На случай, если вы забыли обход в порядке, это: Посетите левый узел, затем корневой узел, затем правый узел)
Довольно просто, теперь давайте перейдем к тому, как он используется при создании многопоточного двоичного дерева:
Шаги к Сделать резьбовое дерево:- Начнем обход и пройдем до самого левого узла дерева:
В этом самом левом узле 5. Предшественник Inorder 5 равен NULL; таким образом, он указывает на NULL, а последователем Inorder 5 является 7, поэтому правый указатель значения узла 5 указывает на 7. изображение, рекурсивно возвращаясь к корневому узлу (7), проверяет наличие нужного узла. В этом случае правый узел узла со значением 7 равен 8. Сначала мы проверим левый указатель узла; если он NULL, то мы укажем его на преемник узла, который равен 7. Для правильного указателя мы проверим, указывает ли он на NULL, затем мы изменим ссылку на узел-преемник, который равен 10, таким образом , он будет указывать на 10.
Предшественник Inorder 5 равен NULL; таким образом, он указывает на NULL, а последователем Inorder 5 является 7, поэтому правый указатель значения узла 5 указывает на 7. изображение, рекурсивно возвращаясь к корневому узлу (7), проверяет наличие нужного узла. В этом случае правый узел узла со значением 7 равен 8. Сначала мы проверим левый указатель узла; если он NULL, то мы укажем его на преемник узла, который равен 7. Для правильного указателя мы проверим, указывает ли он на NULL, затем мы изменим ссылку на узел-преемник, который равен 10, таким образом , он будет указывать на 10.
3. Аналогично для 25 :
4. Аналогичная логика для 30 . Поскольку это самый правый узел дерева, его правый указатель будет указывать на NULL.
Время кодирования !!Давайте посмотрим на программную реализацию Python вышеприведенного дерева потоков:
Узел класса:
def __init__(self,key):
self.left = None
self.right = None
self.val = keyif __name__ == "__main__":
очередь = []
счетчик = 0
корень = узел (10)
корень.левый = узел(7)
корень.правый = узел(25)
корень.левый.левый = узел(5)
корень.левый.правый = узел(8)
корень.правый.правый = узел(30 )
На изображении выше я инициализировал узлы и построил древовидную структуру. Я также инициализировал пустую очередь (очередь) и переменную счетчика (мы обсудим, где мы будем использовать переменные очереди и счетчика).
Теперь в приведенном ниже коде мы выполняем неупорядоченный обход дерева, мы сохраняем узлы результатов неупорядоченного обхода в очереди, как показано ниже:
def printInorder(root,queue):
if root:
# Рекурсия по левому потомку
printInorder(root.left,queue)# Печать данных узла
print(root.val)
queue.append(root) # Рекурсия по правому дочернему элементу
printInorder(root.right,queue)
СЕЙЧАС, основная логика, создание многопоточного двоичного дерева :
def createThreadedTree(root,queue,counter):
if root == None:
вернуть
, если root.left не None:
createThreadedTree(root.left,queue,counter)
counter += 1
else:
if counter == 0:
root.left = None
else:
node = queue.pop(0)
root.left = node
если root.right не None:
createThreadedTree (root.right,queue,counter)
else:
node = queue.pop(0)
if len(queue) > 0:
root.right = queue[0]
else:
root.right = None
Ниже приведено объяснение приведенного выше кода для создания многопоточного дерева:
Реализация Python для создания многопоточного двоичного дереваСтрока 4 - 5: рекурсивно достигают самого левого узла дерева. Строка 6: счетчик увеличивается только тогда, когда он не является самым левым узлом дерева. Строка 8 : Счетчик используется для определения погоды это
самый левый узел или узел, если это так, присвойте ему значение NULL. Строка 11: Если не самый левый узел, то Вытащите элемент из очереди (очередь с неупорядоченным обходом узлов) и назначьте левый указатель узла на Inorder предшественника nodeLine 13 : Аналогично, рекурсивно найдите правильный узел, если правый указатель узла указывает на ноль, затем извлеките элемент из очереди и назначьте преемника Inorder правому указателю этого узла.Строка 17 : Длина очереди используется для определения того, является ли он наиболее дочерним или нет
Теперь, когда мы увидели реализацию создания бинарного дерева с резьбой и его концепцию, в это время у меня в голове возник один вопрос:
Во время обхода, как бы я определить, указывают ли указатели дочернего узла на предшественников/преемников Inorder или они являются родительским узлом, указывающим на его дочерние узлы. Что ж, ответ на это — создать узел с еще двумя тегами 9.0005 Левая метка и Правая метка . Если указатель указывает на дочерний элемент, то мы установим логическое значение левого/правого тега на 1 , иначе, если указатель указывает на предшественника или преемника Inorder, мы установим логическое значение левого/правого тега до 0 .
Таким образом, ниже приведена обновленная реализация создания многопоточного двоичного дерева с левым и правым тегами.
def createThreadedTree (корень, очередь, счетчик):
, если корень == Нет:
вернуть
, если root.left не None:
createThreadedTree(root.left,queue,counter)
counter += 1
else:
# Добавлен левый тег
root.left_tag = 0, если counter == 0:
root .left = None
else:
node = queue.pop(0)
root.left = node
, если root.right не None:
createThreadedTree(root.right,queue,counter)
else:
node = очередь. pop(0)# Добавлен правый тег
root.right_tag = 0if len(queue) > 0:
root.right = queue[0]
else:
root.right = None
В приведенной выше реализации всякий раз, когда дочерний узел указывает на родительский узел, тогда левый/правый тег обновляется до 0 , в зависимости от того, какой указатель указывает на родительский узел.
Ниже приведен код для упорядоченного обхода бинарного дерева с нитями:
def inorderThreadedTree(root):
node = root
#Это переход к самому левому узлу дерева
while(node.left):
node = node.left# это проверка всех узлов
while(node is not None):
# если левые указатели узлов указывают на родительский узел
# тогда выводим значение и переходим к
# правому узлу (родительскому узлу).
# Идентифицируется с помощью left_tag
# (0 означает указание на родительский узел)
if node.left_tag == 0:
print(node.val)
node = node.right
else:
print(node.val)
node = node.right
# если указывает на дочерний узел, продолжайте двигаться к дочернему
# левый узел
if node и node.left_tag == 1:
node = node.left
Уф, вот оно!!
Надеюсь, мне удалось объяснить все, что я понял о многопоточном двоичном дереве. Пожалуйста, дайте мне знать, если логика/код нуждается в некоторых модификациях или если вы хотели бы предложить лучшую реализацию многопоточного двоичного дерева. Я был бы более чем счастлив прочитать ваши предложения.
Структуры данных — это УДОВОЛЬСТВИЕ! УДАЧНОГО КОДИРОВАНИЯ !!
Серия Build the Forest in Python: Make the Forest Thread-Safe
[Обновлено: 27 января 2022 г. ]
]
Многопоточность — распространенный способ повышения производительности. Однако общее состояние и данные между потоками становятся уязвимыми для повреждения, если общее состояние или данные могут быть изменены. Деревья, которые мы построили в серии Build the Forest, не являются потокобезопасными. Когда несколько потоков выполняют операции записи (например, вставку или удаление) одновременно, деревья могут быть повреждены или построены неправильно. Даже операции чтения могут возвращать неверные результаты, когда несколько потоков одновременно выполняют операции записи и чтения. Тема этой статьи — сделать деревья потокобезопасными и обсудить влияние потокобезопасности.
Содержание
Глобальная блокировка интерпретатора (GIL) — это механизм, используемый интерпретатором CPython (тот, который мы загружаем с официального сайта Python, называется CPython), чтобы гарантировать, что только один поток может одновременно выполнять байт-код Python. Хотя GIL гарантирует, что только один поток одновременно выполняет байт-код Python, это не означает, что программы Python, которые мы пишем, автоматически являются потокобезопасными. Это потому, что защита происходит только на уровне байт-кода. Например, следующий фрагмент кода представляет собой байт-код частичной дизассемблирования функции вставки дерева AVL. (Обратите внимание, что мы можем использовать модуль dis для дизассемблирования байт-кода Python)
Это потому, что защита происходит только на уровне байт-кода. Например, следующий фрагмент кода представляет собой байт-код частичной дизассемблирования функции вставки дерева AVL. (Обратите внимание, что мы можем использовать модуль dis для дизассемблирования байт-кода Python)
Дизассемблирование <вставки объекта кода по адресу 0x7f136b391920, файл "forest/binary_trees/avl_tree.py", строка 112>:
128 0 LOAD_GLOBAL 0 (узел)
2 LOAD_FAST 1 (ключ)
4 LOAD_FAST 2 (данные)
6 LOAD_CONST 1 (('ключ', 'данные'))
8 CALL_FUNCTION_KW 2
10 STORE_FAST 3 (новый_узел)
129 12 LOAD_CONST 2 (Нет)
14 STORE_FAST 4 (родительский)
130 16 LOAD_FAST 0 (само)
18 LOAD_ATTR 1 (корень)
20 STORE_FAST 5 (текущий)
…
147 >> 128 LOAD_FAST 3 (новый_узел)
130 LOAD_FAST 4 (родительский)
132 STORE_ATTR 4 (справа)
154 >> 134 LOAD_FAST 4 (родительский)
136 LOAD_ATTR 3 (слева)
138 POP_JUMP_IF_FALSE 146
140 LOAD_FAST 4 (родительский)
142 LOAD_ATTR 4 (справа)
144 POP_JUMP_IF_TRUE 156
155 > > 146 LOAD_FAST 0 (само)
148 LOAD_METHOD 8 (_insert_fixup)
150 LOAD_FAST 3 (новый_узел)
152 ВЫЗОВ_МЕТОД 1
154 POP_TOP
… Когда несколько потоков вызывают функцию вставки дерева AVL, интерпретатор Python может отключить один поток до того, как поток выполнит инструкцию _insert_fixup (т. е. 148 LOAD_METHOD ). В то же время появляется другой поток и выполняет некоторые инструкции байт-кода функции вставки. Если вставка завершена, второй поток прерывает предыдущую функцию вставки. Этот сценарий может привести к неправильному AVL-дереву или, что еще хуже, к сбою программы.
е. 148 LOAD_METHOD ). В то же время появляется другой поток и выполняет некоторые инструкции байт-кода функции вставки. Если вставка завершена, второй поток прерывает предыдущую функцию вставки. Этот сценарий может привести к неправильному AVL-дереву или, что еще хуже, к сбою программы.
Примеры небезопасных потоков
Следуя приведенному выше обсуждению, существует два сценария, когда многопоточность может стать небезопасной: конфликт при записи и конфликт при чтении-записи. Первый означает, что несколько операций записи одновременно управляют общими изменяемыми ресурсами; последнее означает, что операции чтения считывают некоторые ресурсы, которые одновременно обновляются операциями записи.
Сценарий 1 — Конфликт при записи
Для имитации сценария нам необходимо одновременно выполнить несколько операций записи. В этом примере мы будем использовать пять потоков для одновременной вставки 500 неповторяющихся данных. Например, первый поток вставляет данные от 0 до 9.
Switch Interval
Начиная с Python 3.2, была введена функция setswitchinterval, которая позволяет нам устанавливать интерпретатору интервал переключения потоков. Значение определяет продолжительность квантов времени, выделенных для одновременно работающих потоков. Чтобы проблемы многопоточности (например, состояние гонки) возникали быстро, мы используем устанавливает функцию switchinterval , чтобы уменьшить интервал переключения до крошечного значения, чтобы переключение потоков между инструкциями байт-кода происходило намного быстрее.
Следующий код является примером моделирования проблемы с использованием дерева AVL, которое мы создали в разделе «Сборка серии Forest: дерево AVL».
Код примера Thread-Unsafe
import threading импорт системы от ввода списка импорта из forest.binary_trees импортировать avl_tree из обхода импорта forest.binary_trees # Используйте очень маленький интервал переключения потоков, чтобы увеличить вероятность того, что # мы можем легко выявить проблему многопоточности. sys.setswitchinterval (0,0000001) def insert_data (дерево: avl_tree.AVLTree, данные: список) -> Нет: """Вставить данные в дерево.""" для ввода данных: tree.insert (ключ = ключ, данные = строка (ключ)) def multithreading_simulator (дерево: avl_tree.AVLTree) -> Нет: """Используйте пять потоков для вставки данных в дерево с неповторяющимися данными.""" пытаться: поток1 = поток.Поток( target=insert_data, args=(дерево, [элемент для элемента в диапазоне (100)]) ) поток2 = поток.Поток( target=insert_data, args=(дерево, [элемент для элемента в диапазоне (100, 200)]) ) thread3 = поток.Thread( target=insert_data, args=(дерево, [элемент для элемента в диапазоне (200, 300)]) ) thread4 = поток.
Thread( target=insert_data, args=(дерево, [элемент для элемента в диапазоне (300, 400)]) ) thread5 = многопоточность.Thread( target=insert_data, args=(дерево, [элемент для элемента в диапазоне (400, 500)]) ) thread1.start() thread2.start() thread3.start() thread4.start() thread5.start() thread1.присоединиться() thread2.присоединиться() thread3.присоединиться() thread4.присоединиться() thread5.присоединиться() результат = [элемент для элемента в traversal.inorder_traverse(tree=tree)] некорректный_узел_список = список() для индекса в диапазоне (len (результат)): если индекс > 0: если результат[индекс] < результат[индекс - 1]: неправильный_node_list.append( f"{результат[индекс - 1]} -> {результат[индекс]}" ) если len(result) != 500 или len(incorrect_node_list) > 0: print(f"total_nodes: {len(результат)}") print(f"incorrect_order: {incorrect_node_list}") кроме: print("Дерево построено неправильно") если __name__ == "__main__": дерево = avl_tree.
AVLTree() multithreading_simulator (дерево = дерево)
После того, как потоки вставят 500 данных (от 0 до 499), этот пример выполняет несколько проверок:
- Если общее количество узлов равно 500.
- Если выход упорядоченного обхода в порядке.
- Не исключение.
Если какая-либо из этих проверок не пройдена, дерево построено неправильно. Таким образом, мы доказали, что реализованное ранее дерево AVL не является потокобезопасным.
Если мы запустим пример достаточное количество раз (проблемы многопоточности — это проблемы со временем; они могут происходить не всегда), проверки в конечном итоге завершатся ошибкой и будут выглядеть так, как показано в примере ниже.
всего_узлов: 454 некорректный_порядок: ["(459, '459') -> (319, '319')"]
Или Дерево построено неправильно , если возникло какое-либо исключение.
То же самое относится и ко всем другим деревьям, которые мы построили ранее в серии «Построй лес». Полный небезопасный для потоков код доступен по адресу multithreading_not_safe.py.
Полный небезопасный для потоков код доступен по адресу multithreading_not_safe.py.
Сценарий 2. Конфликт при чтении и записи
Хотя операции чтения не изменяют состояние каких-либо ресурсов, на состояние могут влиять операции записи во время чтения операции чтения. Например, поток A ищет узел N, в то время как поток B удаляет узел M, и в процессе удаления поток B также перемещает узел N в другое место. В этом случае поток A может не найти узел N. Следующий код моделирует эту ситуацию.
импорт резьбы
импорт системы
набрав import Any, List
из forest.binary_trees импортировать avl_tree
# Используйте очень маленький интервал переключения потоков, чтобы увеличить вероятность того, что
# мы можем легко выявить проблему многопоточности.
sys.setswitchinterval (0,0000001)
flag = False # Флаг для определения остановки или продолжения потока чтения.
def delete_data (дерево: avl_tree.AVLTree, данные: список) -> Нет:
"""Удалить данные из дерева."""
для ввода данных:
дерево. удалить(ключ=ключ)
def find_node (дерево: avl_tree.AVLTree, ключ: любой) -> нет:
"""Поиск определенного узла."""
пока флаг:
если не дерево.поиск(ключ):
print(f" Не удалось найти узел: {key}")
def multithreading_simulator (дерево: avl_tree.AVLTree, tree_size: int) -> Нет:
"""Используйте один поток для удаления данных и один поток для запроса одновременно."""
глобальный флаг
флаг = Истина
delete_thread = threading.Thread(
target=delete_data, args=(tree, [item for item in range(20, tree_size)])
)
ключ_узла_запроса = 17
query_thread = threading.Thread(target=find_node, args=(дерево, query_node_key))
delete_thread.start()
query_thread.start()
delete_thread.join()
флаг = Ложь
query_thread.join()
print(f"Проверить, существует ли узел {query_node_key}?")
если дерево.поиск(ключ=query_node_key):
print(f"{query_node_key} существует")
если __name__ == "__main__":
print("Построить дерево AVL")
дерево = avl_tree.
удалить(ключ=ключ)
def find_node (дерево: avl_tree.AVLTree, ключ: любой) -> нет:
"""Поиск определенного узла."""
пока флаг:
если не дерево.поиск(ключ):
print(f" Не удалось найти узел: {key}")
def multithreading_simulator (дерево: avl_tree.AVLTree, tree_size: int) -> Нет:
"""Используйте один поток для удаления данных и один поток для запроса одновременно."""
глобальный флаг
флаг = Истина
delete_thread = threading.Thread(
target=delete_data, args=(tree, [item for item in range(20, tree_size)])
)
ключ_узла_запроса = 17
query_thread = threading.Thread(target=find_node, args=(дерево, query_node_key))
delete_thread.start()
query_thread.start()
delete_thread.join()
флаг = Ложь
query_thread.join()
print(f"Проверить, существует ли узел {query_node_key}?")
если дерево.поиск(ключ=query_node_key):
print(f"{query_node_key} существует")
если __name__ == "__main__":
print("Построить дерево AVL")
дерево = avl_tree. AVLTree()
размер_дерева = 200
для ключа в диапазоне (tree_size):
tree.insert (ключ = ключ, данные = строка (ключ))
print("Тест многопоточного чтения/записи")
multithreading_simulator (дерево = дерево, размер_дерева = размер_дерева)
AVLTree()
размер_дерева = 200
для ключа в диапазоне (tree_size):
tree.insert (ключ = ключ, данные = строка (ключ))
print("Тест многопоточного чтения/записи")
multithreading_simulator (дерево = дерево, размер_дерева = размер_дерева) В этом примере мы сначала строим дерево с 200 узлами, а затем используем один поток для продолжения поиска узла 17, в то время как другой поток удаляет узлы с 20 по 200. Поскольку в примере не удаляется узел 17, поток поиска должен найти узел 17 постоянно. Кроме того, после завершения потока удаления мы снова запрашиваем узел 17, чтобы убедиться, что узел 17 все еще существует в дереве. Если в какой-то момент поток поиска не может найти узел 17, это означает, что мы доказываем, что ранее реализованное дерево AVL не является потокобезопасным в ситуации конфликта чтения-записи. И это легко сделать, если мы запустим пример достаточное количество раз. Когда это произойдет, появится следующий вывод.
Построить дерево AVL Многопоточный тест чтения/записи Не удалось найти узел: 17 Проверить, существует ли узел 17? 17 exists
В соответствии с тем же стилем и предположением, что и в других статьях серии Build the Forest, реализация предполагает Python 3. 9 или более позднюю версию. Эта статья добавляет в наш проект два модуля: atomic_trees.py для реализации атомарных деревьев и test_automic_trees.py для модульных тестов. После добавления этих двух файлов макет нашего проекта становится следующим:
9 или более позднюю версию. Эта статья добавляет в наш проект два модуля: atomic_trees.py для реализации атомарных деревьев и test_automic_trees.py для модульных тестов. После добавления этих двух файлов макет нашего проекта становится следующим:
лесной питон
├── лес
│ ├── __init__.py
│ ├── бинарные_деревья
│ │ ├── __init__.py
│ │ ├── atomic_trees.py
│ │ ├── avl_tree.py
│ │ ├── binary_search_tree.py
│ │ ├── double_threaded_binary_tree.py
│ │ ├── red_black_tree.py
│ │ ├── single_threaded_binary_trees.py
│ │ └── traversal.py
│ ├── metrics.py
│ └── tree_exceptions.py
└── тесты
├── __init__.py
├── conftest.py
├── test_atomic_trees.py
├── test_avl_tree.py
├── test_binary_search_tree.py
├── test_double_threaded_binary_tree.py
├── test_metrics.py
├── test_red_black_tree.py
├── test_single_threaded_binary_trees.py
└── test_traversal.py (полный код доступен на сайте forest-python)
Чтобы сделать лес потокобезопасным, нам необходимо предотвратить конфликты при записи и чтении-записи.
Что мы хотим защитить?
Первое, что мы можем спросить, что защищать? В общем, нам нужно охватить любое общее изменяемое состояние и данные. Древовидная структура данных представляет собой композицию с узлами дерева. Любое изменение узла обновляет состояние дерева, а узлы дерева являются общими и изменяемыми. Следовательно, чтобы быть потокобезопасным, нам нужно обеспечить, чтобы переход узлов дерева не прерывался.
В общем, нам не нужно беспокоиться об операциях только для чтения, потому что операции чтения ничего не изменяют. Только две функции изменят состояние деревьев, которые мы построили в серии: вставка и удаление. Возьмем в качестве примера вставку дерева AVL. На следующем рисунке показаны узлы, затронутые после вставки узла 35.
Из этого примера видно, что во время операций вставки обновляются несколько узлов. Если есть какой-либо другой поток, который касается этих узлов (например, 23, 33 и 37) или изменяет другие узлы, которые также влияют на свойства (например, высоту и коэффициент баланса) узлов, 22, 33 и 37 во время вставки , вставка создаст неправильное дерево AVL или, что еще хуже, программа вылетит.
Тот же сценарий можно применить и к удалению. Поэтому нам необходимо убедиться, что и вставка, и удаление могут выполняться без каких-либо помех. Другими словами, функции вставки и удаления являются критическим разделом, который не может выполняться более чем одним потоком одновременно.
Как насчет функций фиксации, трансплантации и вращения?
Эти функции также обновляют состояние деревьев. Однако их назначение — поддерживать вставку и удаление, поэтому они определены как внутренние функции (т. е. клиентский код не должен вызывать их напрямую). Пока мы гарантируем, что выполняем вставку или удаление по одному, доступ к этим вспомогательным функциям осуществляется только одним потоком за раз — их не нужно защищать.
Как защитить?
Одним из распространенных решений для предотвращения одновременного доступа к общему ресурсу является взаимное исключение. Мы можем использовать встроенные в Python объекты блокировки для защиты критической секции: поток должен получить блокировку перед входом в критическую секцию и снять блокировку после выхода из критической секции. Используйте вставку дерева AVL в качестве примера. Мы можем обновить алгоритм вставки, чтобы он был потокобезопасным, добавив эти шаги.
Используйте вставку дерева AVL в качестве примера. Мы можем обновить алгоритм вставки, чтобы он был потокобезопасным, добавив эти шаги.
- Получить замок.
- Вставьте новый узел с высотой 0 так же, как вставка бинарного дерева поиска: найдите правильное место (т. е. родителя нового узла) для вставки нового узла, пройдясь по дереву от корня и сравнив ключ нового узла с ключом каждого узла на этом пути.
- Обновите высоту и проверьте, происходит ли нарушение свойства AVL-дерева путем обратной трассировки от нового узла к корню. Возвращаясь к корню, при необходимости обновите высоту каждого узла на пути. Если мы находим несбалансированный узел, выполняем определенные повороты, чтобы сбалансировать его. После вращения вставка завершается. Если несбалансированный узел не найден, вставка завершается после достижения корня и обновления его высоты.
- Разблокируйте замок.
Вторая и третья ступени являются критическими секциями и теперь защищены замковым механизмом. Поскольку функция атомарной вставки не меняет своей исходной функциональности, мы можем реализовать атомарное дерево AVL как производный класс от исходного дерева AVL и расширить вставку, как показано ниже.
Поскольку функция атомарной вставки не меняет своей исходной функциональности, мы можем реализовать атомарное дерево AVL как производный класс от исходного дерева AVL и расширить вставку, как показано ниже.
импортная резьба
от ввода импорта Любой, Необязательно
из forest.binary_trees импортировать avl_tree
класс AVLTree (avl_tree.AVLTree):
def __init__(я, реестр: необязательно [metrics.MetricRegistry] = None) -> None:
avl_tree.AVLTree.__init__(я, реестр=реестр)
self._lock = threading.Lock() # Объект блокировки
def insert(self, key: Any, data: Any) -> None:
self._lock.acquire()
# Исходная функция вставки - это критический раздел, и
# защищен замком.
avl_tree.AVLTree.insert(я, ключ=ключ, данные=данные)
self._lock.release() Использование блокировок в с оператором
Хорошая практика в программировании на Python заключается в том, что если блок кода должен управлять ресурсами (например, открыть/закрыть файл или получить/снять блокировку), мы всегда должны используйте контекстный менеджер with-statement. Блок кода, заключенный в оператор with , гарантированно освободит ресурс (например, блокировки), даже если в операторе with возникнет исключение (подробности см. в разделе Использование блокировок в операторе with). Имея в виду передовой опыт, мы можем обновить приведенную выше реализацию, используя с оператором для управления ресурсом блокировки. Мы также можем защитить удаление таким же образом. Кроме того, синтаксис также упрощает реализацию, как показано ниже.
Блок кода, заключенный в оператор with , гарантированно освободит ресурс (например, блокировки), даже если в операторе with возникнет исключение (подробности см. в разделе Использование блокировок в операторе with). Имея в виду передовой опыт, мы можем обновить приведенную выше реализацию, используя с оператором для управления ресурсом блокировки. Мы также можем защитить удаление таким же образом. Кроме того, синтаксис также упрощает реализацию, как показано ниже.
импортная резьба
от ввода импорта Любой, Необязательно
из forest.binary_trees импортировать avl_tree
класс AVLTree (avl_tree.AVLTree):
def __init__(я, реестр: необязательно [metrics.MetricRegistry] = None) -> None:
avl_tree.AVLTree.__init__(я, реестр=реестр)
self._lock = многопоточность.Lock()
def insert(self, key: Any, data: Any) -> None:
с self._lock:
avl_tree.AVLTree.insert(я, ключ=ключ, данные=данные)
def delete(self, key: Any) -> None:
с self. _lock:
avl_tree.AVLTree.delete(я, ключ=ключ)
_lock:
avl_tree.AVLTree.delete(я, ключ=ключ) Как насчет конкуренции чтения-записи?
До сих пор сделанное выше изменение защищало дерево от ситуации конфликта записи, но не предотвращало конфликт чтения-записи. Самое простое решение такое же, как и с функциями вставки и удаления — с помощью механизма блокировки. Однако может возникнуть тупиковая ситуация, если мы неосторожно используем механизм блокировки. На картинке ниже показан случай. Левая сторона — это атомарное дерево AVL с блокировкой в функции поиска, а правая сторона — исходное дерево AVL, из которого происходит атомарное дерево AVL.
Когда клиент вызывает функцию удаления атомарного дерева AVL, он сначала получает блокировку, а затем вызывает функцию удаления своего родителя (т. е. функцию удаления из исходного дерева AVL). Когда мы реализовали функцию удаления исходного дерева AVL, мы использовали функцию поиска дерева, чтобы определить удаляемый узел. Однако, поскольку функция удаления вызывается из атомарного дерева AVL (т. е. производного класса), вызываемой функцией поиска будет функция поиска атомарного дерева AVL. И первое, что пытается сделать поиск атомарного дерева AVL, — это получить блокировку, чего никогда не произойдет, потому что вызывающая сторона (т. е. функция удаления атомарного дерева AVL) все еще удерживает блокировку. Вот так и возник тупик.
е. производного класса), вызываемой функцией поиска будет функция поиска атомарного дерева AVL. И первое, что пытается сделать поиск атомарного дерева AVL, — это получить блокировку, чего никогда не произойдет, потому что вызывающая сторона (т. е. функция удаления атомарного дерева AVL) все еще удерживает блокировку. Вот так и возник тупик.
Есть много способов справиться с тупиковой ситуацией. Решение, которое мы должны использовать, заключается в разделении интерфейса функции search и реализации в исходном дереве AVL — новая функция _search содержит реализацию поиска, а функция interface search вызывает функцию _search , как показано ниже. .
поиск по определению (я, ключ: Любой) -> Дополнительно [Узел]:
вернуть self._search (ключ = ключ)
def _search(self, key: Any) -> Дополнительно[Узел]:
текущий = self.root
пока текущий:
если ключ < текущий.ключ:
текущий = текущий.слева
Элиф ключ > текущий. ключ:
текущий = текущий.справа
else: # Ключ найден
обратный ток
возврат Нет
ключ:
текущий = текущий.справа
else: # Ключ найден
обратный ток
возврат Нет Любой метод, которому необходимо вызвать функцию поиска, вызовет функцию реализации _search вместо интерфейса search . Таким образом, функция удаления исходного дерева AVL становится следующей.
def delete(self, key: Any) -> None:
если self.root и (deleting_node := self._search(key=key)):
# Остальной код остается прежним
… Несколько причин для этого. Прежде всего, поскольку интерфейс остается прежним, это не повлияет на клиентский код, вызывающий исходное дерево AVL. Во-вторых, мы избегаем дублирования кода. В-третьих, мы упрощаем реализацию потокобезопасной функции поиска в атомарном дереве AVL. Ниже приведена реализация атомарного дерева AVL.
класс AVLTree(avl_tree.AVLTree):
"""Дерево AVL с защитой от многопоточности."""
def __init__(я, реестр: необязательно [metrics.MetricRegistry] = None) -> None:
avl_tree. AVLTree.__init__(я, реестр=реестр)
self._lock = многопоточность.Lock()
def search(self, key: Any) -> Дополнительно[avl_tree.Node]:
"""Потокобезопасный поиск."""
с self._lock:
вернуть avl_tree.AVLTree.search (я, ключ = ключ)
def insert(self, key: Any, data: Any) -> None:
"""Потокобезопасная вставка."""
с self._lock:
avl_tree.AVLTree.insert(я, ключ=ключ, данные=данные)
def delete(self, key: Any) -> None:
"""Поточное удаление."""
с self._lock:
avl_tree.AVLTree.delete(я, ключ=ключ)
AVLTree.__init__(я, реестр=реестр)
self._lock = многопоточность.Lock()
def search(self, key: Any) -> Дополнительно[avl_tree.Node]:
"""Потокобезопасный поиск."""
с self._lock:
вернуть avl_tree.AVLTree.search (я, ключ = ключ)
def insert(self, key: Any, data: Any) -> None:
"""Потокобезопасная вставка."""
с self._lock:
avl_tree.AVLTree.insert(я, ключ=ключ, данные=данные)
def delete(self, key: Any) -> None:
"""Поточное удаление."""
с self._lock:
avl_tree.AVLTree.delete(я, ключ=ключ) Та же ситуация происходит с другими деревьями, которые мы реализовали ранее. Следовательно, мы можем применить ту же идею для реализации остальных деревьев. Полные атомарные деревья доступны по адресу atomic_trees.py, а их родители также изменяются путем разделения интерфейса функции поиска и реализации. Завершенные обновления см. в списке измененных файлов.
У нас всегда должно быть как можно больше модульных тестов для нашего кода. Поскольку мы доказали, что исходное дерево AVL (на примере дерева AVL) не является потокобезопасным, мы могли бы запустить те же тесты, чтобы убедиться, что атомарное дерево AVL является потокобезопасным как от конфликтов записи, так и от конфликтов чтения-записи. Точно так же мы можем запустить те же тесты для остальных атомарных деревьев. Проверьте test_atomic_trees.py для полного модульного теста.
Поскольку мы доказали, что исходное дерево AVL (на примере дерева AVL) не является потокобезопасным, мы могли бы запустить те же тесты, чтобы убедиться, что атомарное дерево AVL является потокобезопасным как от конфликтов записи, так и от конфликтов чтения-записи. Точно так же мы можем запустить те же тесты для остальных атомарных деревьев. Проверьте test_atomic_trees.py для полного модульного теста.
Хотя атомарные деревья потокобезопасны, использование блокировок требует затрат. Этот механизм обеспечивает последовательный доступ к критической секции (например, к функциям вставки и удаления). Мотивация многопоточного программирования заключается в повышении производительности. Когда код должен выполняться последовательно, мы теряем преимущества многопоточности. Кроме того, в мире Python (то есть, в частности, CPython) GIL также играет важную роль в многопоточном программировании. В некоторых случаях GIL снижает производительность, получаемую от многопоточного подхода. В оставшейся части этого раздела будет использоваться дерево AVL (как исходное дерево AVL (т. е. дерево AVL, не поддерживающее потоки), так и атомарное дерево AVL) для оценки влияния на производительность механизма блокировки и GIL в многопоточных ситуациях.
е. дерево AVL, не поддерживающее потоки), так и атомарное дерево AVL) для оценки влияния на производительность механизма блокировки и GIL в многопоточных ситуациях.
Кроме того, мы можем сравнить функцию поиска только между исходным деревом AVL и атомарным деревом AVL, потому что вставка и удаление не являются потокобезопасными в исходном дереве AVL. Чтобы измерить влияние на производительность, мы выполним следующие действия:
- Определим исходное дерево AVL с 200 000 узлов и проведем поиск по каждому узлу с помощью одного потока. И измерьте время, затраченное на это.
- Используйте то же дерево AVL из шага 2, но используйте два потока для поиска 200 000 узлов — один поток выполняет поиск узлов с 0 по 99 999, а другой поток запрашивает от 100 000 до 199 999. И измерьте время, затраченное на это.
- Определите атомарное дерево AVL с 200 000 узлов и используйте два потока для поиска по 200 000 узлов. Кроме того, один поток от 0 до 99 999, а другой поток от 100 000 до 199 999.
 И измерьте время, затраченное на это.
И измерьте время, затраченное на это.
Сравнивая результаты шага 1 и шага 2, мы можем увидеть влияние GIL. А сравнение результатов шагов 2 и 3 дает представление о влиянии на производительность за счет использования механизма блокировки. Ниже приведен пример кода.
импорт резьбы
время импорта
от ввода списка импорта
из forest.binary_trees импортировать avl_tree
из forest.binary_trees импортировать atomic_trees
def query_data (дерево: avl_tree.AVLTree, данные: список) -> Нет:
"""Запрос узлов из дерева."""
для ввода данных:
дерево.поиск(ключ=ключ)
def multithreading_simulator (дерево: avl_tree.AVLTree, total_nodes: int) -> float:
"""Используйте два потока для запроса узлов с разными диапазонами."""
поток1 = поток.Поток(
target=query_data, args=(tree, [item for item in range(total_nodes // 2)])
)
поток2 = поток.Поток(
цель = данные_запроса,
args=(tree, [item for item in range(total_nodes // 2, total_nodes)]),
)
начало = время. время()
thread1.start()
thread2.start()
thread1.присоединиться()
thread2.присоединиться()
конец = время.время()
вернуться конец - начало
если __name__ == "__main__":
всего_узлов = 200000
original_avl_tree = avl_tree.AVLTree()
# Случай с одним потоком
для ключа в диапазоне (total_nodes):
original_avl_tree.insert (ключ = ключ, данные = строка (ключ))
data = [элемент для элемента в диапазоне (total_nodes)]
начало = время.время()
query_data (дерево = исходное_avl_tree, данные = данные)
конец = время.время()
дельта = конец - начало
print("Случай с одним потоком")
print(f"Время в секундах: {дельта}")
# Случай многопоточности
delta_with_threads = многопоточный_симулятор(
дерево = исходное_avl_дерево, total_nodes = total_nodes
)
print("Многопоточный случай")
print(f"Время в секундах: {delta_with_threads}")
# Многопоточность с замком
avl_tree_with_lock = атомарные_деревья.AVLTree()
для ключа в диапазоне (total_nodes):
avl_tree_with_lock.
время()
thread1.start()
thread2.start()
thread1.присоединиться()
thread2.присоединиться()
конец = время.время()
вернуться конец - начало
если __name__ == "__main__":
всего_узлов = 200000
original_avl_tree = avl_tree.AVLTree()
# Случай с одним потоком
для ключа в диапазоне (total_nodes):
original_avl_tree.insert (ключ = ключ, данные = строка (ключ))
data = [элемент для элемента в диапазоне (total_nodes)]
начало = время.время()
query_data (дерево = исходное_avl_tree, данные = данные)
конец = время.время()
дельта = конец - начало
print("Случай с одним потоком")
print(f"Время в секундах: {дельта}")
# Случай многопоточности
delta_with_threads = многопоточный_симулятор(
дерево = исходное_avl_дерево, total_nodes = total_nodes
)
print("Многопоточный случай")
print(f"Время в секундах: {delta_with_threads}")
# Многопоточность с замком
avl_tree_with_lock = атомарные_деревья.AVLTree()
для ключа в диапазоне (total_nodes):
avl_tree_with_lock. insert (ключ = ключ, данные = строка (ключ))
delta_with_lock = многопоточный_симулятор(
дерево = avl_tree_with_lock, total_nodes = total_nodes
)
print("Многопоточность с замком")
print(f"Время в секундах: {delta_with_lock}")
insert (ключ = ключ, данные = строка (ключ))
delta_with_lock = многопоточный_симулятор(
дерево = avl_tree_with_lock, total_nodes = total_nodes
)
print("Многопоточность с замком")
print(f"Время в секундах: {delta_with_lock}") После запуска примера мы получим время выполнения для каждого случая.
Корпус с одной резьбой Время в секундах: 0,3944363594055176 Многопоточный случай Время в секундах: 0,4100222587585449 Многопоточность с замком Время в секундах: 2,7478058338165283
(Обратите внимание, что результирующее число зависит от машины. Однако сравнение между тремя случаями должно быть одинаковым на любом устройстве.)
Здесь мы видим, что прирост производительности с двумя потоками значительно ограниченный или даже отрицательный от одного потока к двум потокам (результаты от первого и второго). Сравнивая второй и третий результаты, мы также понимаем, что стоимость использования замкового механизма относительно высока.
Использование атомарных деревьев аналогично использованию исходных деревьев.

 Таким образом экономится место.
Таким образом экономится место. right = None
right = None  left не None:
left не None:  Строка 17 : Длина очереди используется для определения того, является ли он наиболее дочерним или нет
Строка 17 : Длина очереди используется для определения того, является ли он наиболее дочерним или нет 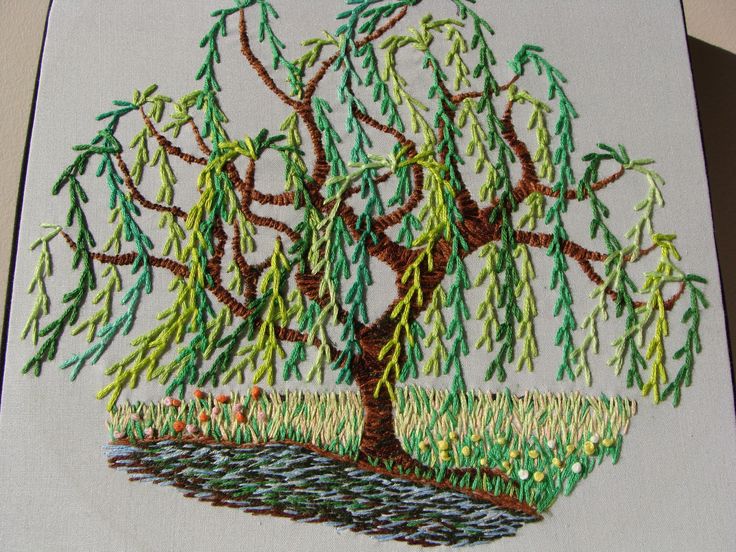 left):
left):  binary_trees импортировать avl_tree
из обхода импорта forest.binary_trees
# Используйте очень маленький интервал переключения потоков, чтобы увеличить вероятность того, что
# мы можем легко выявить проблему многопоточности.
sys.setswitchinterval (0,0000001)
def insert_data (дерево: avl_tree.AVLTree, данные: список) -> Нет:
"""Вставить данные в дерево."""
для ввода данных:
tree.insert (ключ = ключ, данные = строка (ключ))
def multithreading_simulator (дерево: avl_tree.AVLTree) -> Нет:
"""Используйте пять потоков для вставки данных в дерево с неповторяющимися данными."""
пытаться:
поток1 = поток.Поток(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (100)])
)
поток2 = поток.Поток(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (100, 200)])
)
thread3 = поток.Thread(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (200, 300)])
)
thread4 = поток.
binary_trees импортировать avl_tree
из обхода импорта forest.binary_trees
# Используйте очень маленький интервал переключения потоков, чтобы увеличить вероятность того, что
# мы можем легко выявить проблему многопоточности.
sys.setswitchinterval (0,0000001)
def insert_data (дерево: avl_tree.AVLTree, данные: список) -> Нет:
"""Вставить данные в дерево."""
для ввода данных:
tree.insert (ключ = ключ, данные = строка (ключ))
def multithreading_simulator (дерево: avl_tree.AVLTree) -> Нет:
"""Используйте пять потоков для вставки данных в дерево с неповторяющимися данными."""
пытаться:
поток1 = поток.Поток(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (100)])
)
поток2 = поток.Поток(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (100, 200)])
)
thread3 = поток.Thread(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (200, 300)])
)
thread4 = поток. Thread(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (300, 400)])
)
thread5 = многопоточность.Thread(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (400, 500)])
)
thread1.start()
thread2.start()
thread3.start()
thread4.start()
thread5.start()
thread1.присоединиться()
thread2.присоединиться()
thread3.присоединиться()
thread4.присоединиться()
thread5.присоединиться()
результат = [элемент для элемента в traversal.inorder_traverse(tree=tree)]
некорректный_узел_список = список()
для индекса в диапазоне (len (результат)):
если индекс > 0:
если результат[индекс] < результат[индекс - 1]:
неправильный_node_list.append(
f"{результат[индекс - 1]} -> {результат[индекс]}"
)
если len(result) != 500 или len(incorrect_node_list) > 0:
print(f"total_nodes: {len(результат)}")
print(f"incorrect_order: {incorrect_node_list}")
кроме:
print("Дерево построено неправильно")
если __name__ == "__main__":
дерево = avl_tree.
Thread(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (300, 400)])
)
thread5 = многопоточность.Thread(
target=insert_data, args=(дерево, [элемент для элемента в диапазоне (400, 500)])
)
thread1.start()
thread2.start()
thread3.start()
thread4.start()
thread5.start()
thread1.присоединиться()
thread2.присоединиться()
thread3.присоединиться()
thread4.присоединиться()
thread5.присоединиться()
результат = [элемент для элемента в traversal.inorder_traverse(tree=tree)]
некорректный_узел_список = список()
для индекса в диапазоне (len (результат)):
если индекс > 0:
если результат[индекс] < результат[индекс - 1]:
неправильный_node_list.append(
f"{результат[индекс - 1]} -> {результат[индекс]}"
)
если len(result) != 500 или len(incorrect_node_list) > 0:
print(f"total_nodes: {len(результат)}")
print(f"incorrect_order: {incorrect_node_list}")
кроме:
print("Дерево построено неправильно")
если __name__ == "__main__":
дерево = avl_tree. AVLTree()
multithreading_simulator (дерево = дерево)
AVLTree()
multithreading_simulator (дерево = дерево)  удалить(ключ=ключ)
def find_node (дерево: avl_tree.AVLTree, ключ: любой) -> нет:
"""Поиск определенного узла."""
пока флаг:
если не дерево.поиск(ключ):
print(f" Не удалось найти узел: {key}")
def multithreading_simulator (дерево: avl_tree.AVLTree, tree_size: int) -> Нет:
"""Используйте один поток для удаления данных и один поток для запроса одновременно."""
глобальный флаг
флаг = Истина
delete_thread = threading.Thread(
target=delete_data, args=(tree, [item for item in range(20, tree_size)])
)
ключ_узла_запроса = 17
query_thread = threading.Thread(target=find_node, args=(дерево, query_node_key))
delete_thread.start()
query_thread.start()
delete_thread.join()
флаг = Ложь
query_thread.join()
print(f"Проверить, существует ли узел {query_node_key}?")
если дерево.поиск(ключ=query_node_key):
print(f"{query_node_key} существует")
если __name__ == "__main__":
print("Построить дерево AVL")
дерево = avl_tree.
удалить(ключ=ключ)
def find_node (дерево: avl_tree.AVLTree, ключ: любой) -> нет:
"""Поиск определенного узла."""
пока флаг:
если не дерево.поиск(ключ):
print(f" Не удалось найти узел: {key}")
def multithreading_simulator (дерево: avl_tree.AVLTree, tree_size: int) -> Нет:
"""Используйте один поток для удаления данных и один поток для запроса одновременно."""
глобальный флаг
флаг = Истина
delete_thread = threading.Thread(
target=delete_data, args=(tree, [item for item in range(20, tree_size)])
)
ключ_узла_запроса = 17
query_thread = threading.Thread(target=find_node, args=(дерево, query_node_key))
delete_thread.start()
query_thread.start()
delete_thread.join()
флаг = Ложь
query_thread.join()
print(f"Проверить, существует ли узел {query_node_key}?")
если дерево.поиск(ключ=query_node_key):
print(f"{query_node_key} существует")
если __name__ == "__main__":
print("Построить дерево AVL")
дерево = avl_tree. AVLTree()
размер_дерева = 200
для ключа в диапазоне (tree_size):
tree.insert (ключ = ключ, данные = строка (ключ))
print("Тест многопоточного чтения/записи")
multithreading_simulator (дерево = дерево, размер_дерева = размер_дерева)
AVLTree()
размер_дерева = 200
для ключа в диапазоне (tree_size):
tree.insert (ключ = ключ, данные = строка (ключ))
print("Тест многопоточного чтения/записи")
multithreading_simulator (дерево = дерево, размер_дерева = размер_дерева)  _lock:
avl_tree.AVLTree.delete(я, ключ=ключ)
_lock:
avl_tree.AVLTree.delete(я, ключ=ключ)  ключ:
текущий = текущий.справа
else: # Ключ найден
обратный ток
возврат Нет
ключ:
текущий = текущий.справа
else: # Ключ найден
обратный ток
возврат Нет  AVLTree.__init__(я, реестр=реестр)
self._lock = многопоточность.Lock()
def search(self, key: Any) -> Дополнительно[avl_tree.Node]:
"""Потокобезопасный поиск."""
с self._lock:
вернуть avl_tree.AVLTree.search (я, ключ = ключ)
def insert(self, key: Any, data: Any) -> None:
"""Потокобезопасная вставка."""
с self._lock:
avl_tree.AVLTree.insert(я, ключ=ключ, данные=данные)
def delete(self, key: Any) -> None:
"""Поточное удаление."""
с self._lock:
avl_tree.AVLTree.delete(я, ключ=ключ)
AVLTree.__init__(я, реестр=реестр)
self._lock = многопоточность.Lock()
def search(self, key: Any) -> Дополнительно[avl_tree.Node]:
"""Потокобезопасный поиск."""
с self._lock:
вернуть avl_tree.AVLTree.search (я, ключ = ключ)
def insert(self, key: Any, data: Any) -> None:
"""Потокобезопасная вставка."""
с self._lock:
avl_tree.AVLTree.insert(я, ключ=ключ, данные=данные)
def delete(self, key: Any) -> None:
"""Поточное удаление."""
с self._lock:
avl_tree.AVLTree.delete(я, ключ=ключ)